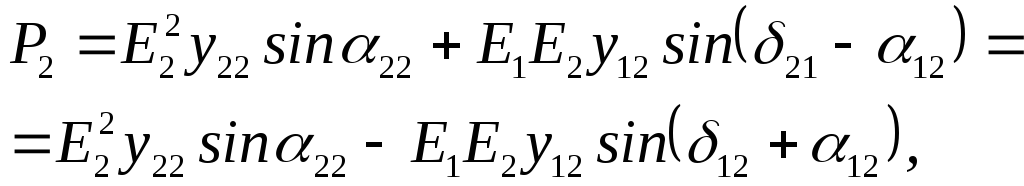2.3. Определение токов

Схема замещения генератора в установившемся режиме включает ЭДС, приложенную за тем или иным сопротивлением (например, ). Пусть к данной системе подключеноmгенераторов. Тогда ток вi-ом генераторе может быть определен как

.

(2.25)

ЭДС генераторов могут быть представлены в полярной форме как

,

(2.26)

где - угол между векторамии(рис.2.13).

Рис. 2.13. Векторная диаграмма ЭДС системы

Поскольку проводимости могут быть представлены в виде

,

(2.27)

где , то выражение (2.24) может быть записано следующим образом

.

(2.28)

Ток i-го генератораможно представить как сумму двух составляющих, одна из которыхнаправлена по, а другая () отстает отна 90°

,

(2.29)

где

и	(2.30)
.	(2.31)

2.4. Определение мощности

Комплекс полной мощности, протекающей через какую либо точку схемы, может быть определен как произведение комплекса ЭДС или напряжения в данной точке на сопряженный комплекс тока. Так, мощность, выдаваемая i-м источником, может быть найдена как

,

(2.32)

где - сопряженный комплекс тока.

Примем, что ось отсчета совпадает с направлением вектора , т.е.,и, тогда

,

(2.33)

но , следовательно

,	(2.34)

где .

Аналогично можно показать, что

.

(2.35)

Рассмотрим простейшую двухмашинную систему (рис. 2.14а), состоящую из двух генераторов, подключенных к электрической сети с нагрузками.

а)	б)
в)

Рис. 2.14. Простейшая двухмашинная система

а – схема; б – характеристики активной и реактивной мощности; в – схема для случая генератора, подключенного к мощной системе

На основании выражений (2.34) и (2.35) для первого генератора можно записать

	(2.36)
.	(2.37)

Аналогично для второго генератора (с учетом того, что )

	(2.38)
	(2.39)

На рис. 2.14б показаны характеристики мощности, соответствующие выражениям (2.36)-(2.37). В общем случае угол может быть как положительным, так и отрицательным. На рис. 2.14б характеристики приведены для.

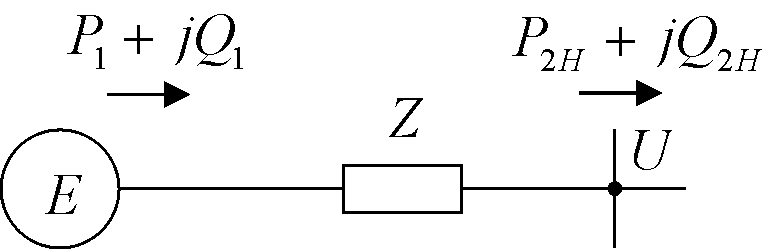
Рассмотрим генератор, подключенный через сопротивление к шинам подстанции системы (рис. 2.14в). Будем считать, что мощность системы настолько велика, что можно пренебречь ее внутренним сопротивлением и принять амплитуду напряженияна шинах подстанции системы неизменной. В этом случае:,и

	(2.40)
,	(2.41)
	(2.42)
,	(2.43)

где .

При неучете активных сопротивлений и проводимостей .

2.5. Максимальные и предельные нагрузки

Максимальные нагрузки– это наибольшие значения, которые могут иметь токи, мощности и напряжения в каком-либо элементе системы.

В качестве примера рассмотрим линию, представленную чисто реактивным сопротивлением . Если напряжения в узлах, к которым подключена линия, равныи, то по аналогии с выражением (2.40) активная мощность, передаваемая по линии

(2.44)

где - угол между векторами напряженийи.

Максимальная мощность, передаваемая по линии при заданных значениях напряжений по ее концам,

(2.45)

Величину часто называютпределом передаваемой мощности. Очевидно, чтопри.

Если линия представлена полным сопротивлением , то

и	(2.46)
.	(2.47)

В этом случае при.

Выражения (2.46) - (2.47) определяют мощность на конце линии, подключенном к первому узлу (т.е. узлу с напряжением ).

Максимальная мощность, передаваемая по линии от генератора к шинам подстанции системы (рис. 2.14в)

.

(2.48)

В этом случае сопротивление включает в себя сопротивление схемы замещения генератора и всех элементов, включенных последовательно между генератором и шинами подстанции с напряжением(линии, трансформатора) - рис. 2.15. Исключить влияние сопротивлений генератора и трансформатора можно применив такое возбуждение генератора, которое было бы способно поддерживать неизменное напряжениена передающем конце линии.

Рис. 2.15. Генератор, подключенный через линию и трансформатор к шинам подстанции системы

Если в сети, связывающей генератор с системой, происходит промежуточный отбор мощности (т.е. к этой сети подключены промежуточные нагрузки), то максимальная мощность отдаваемая генератором

(2.49)

Наличие максимума в значении активной мощности обусловлено только свойствами передачи энергии переменным током и не связано с ограничениями вызванными нагревом токоведущих частей, потерями напряжения, напряжением короны и т.п. Для основных элементов системы (генераторов, трансформаторов, линий и т.п.) определяют предельные нагрузки, т.е. нагрузки, ограниченные значениями отдельных параметров режима (величиной тока статора, тока возбуждения и т.д.). Кроме того, часто используют понятие пропускной способности элемента, понимая под ней наибольшую мощность, которую с учетом всех факторов можно передать через данный элемент.