
- •Початки та кінці обмотки ВН позначають буквами А й X; обмотки НН– буквами а та x.
- •Принцип дії трансформатора оснований на законі електромагнітної індукції (2.11)
- •Рис. 4.3. Перетворення схем заміщення трансформатора:
- •5.Дослідне визначення параметрів приведеної схеми заміщення
- •5.3. Побудова векторної діаграми трансформатора
- •Із трикутника опору КЗ АВС можна записати
- •17. Лабораторна робота
- •ДОСЛІДЖЕННЯ ОДНОФАЗНОГО ТРАНСФОРМАТОРА
- •Основні теоретичні відомості
- •Режим
- •Обчислено

Необхідно зазначити, що у формули таблиці 5.2 входить фазний коефіцієнт трансформації для трифазного трансформатора KФ (див. розділ 6), який залежить від типу з’єднання обмоток трансформатора.
5.3. Побудова векторної діаграми трансформатора
Векторна діаграма – це графічне зображення векторних рівнянь приведеного трансформатора (4.16), (4.22)
|
|
|
|
|
|
; |
|
U1 |
= −E1 |
+ jI1 x1 |
+ I1 R1 |
|
|||
|
|
|
2 |
|
2 |
|
(5.14) |
2 |
2 |
2 |
2 |
|
|||
U ′ = E′ − jI ′ x |
|
− I ′ R′ ; |
|
||||
I |
= I + (−I ′ ). |
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
Векторні рівняння напруг та струмів приведеного трансформатора описують усі режими трансформатора від ХХ до номінального.
Із цих рівнянь можна графічно знайти невідомі, наприклад, вектори
|
|
1 |
|
, якщо відомі всі інші вектори. Процес графічного зображення |
|
|
2 |
,I |
1 |
||
U ′ ,U |
|
|
|
||
цих векторів називається побудовою векторної діаграми. Необхідно пам’ятати, що за додатний напрямок обертання векторів прийнято рух проти годинникової стрілки.
Побудову векторної діаграми починають із вектора Ф (рис. 5.7).
|
|
|
|
jI |
x |
|
|
|
|
|
jI |
x |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|||||
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
I |
|
|
|
|
|
|
|
|
|
|
I |
R |
|
|
|
|
|
|
|
|
R |
|
|
|
|
||
|
|
|
|
|
I |
|
|
|
|
|
|
|
1 |
1 |
|
|
|
||||
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
U1 |
− |
|
|
|
|
|
|
U1 |
|
− |
|
I1 |
|
|
|
|||
|
|
|
|
Е1 |
|
′ |
|
|
|
Е1 |
|
|
′ |
||||||||
|
|
|
|
|
|
|
|
− I |
|
|
|
|
|
|
|
|
− I |
||||
|
|
|
|
|
ψ 1 |
|
2 |
|
|
|
|
|
|
ψ 1 |
|
|
2 |
|
|||
|
|
|
|
|
I0 |
|
|
|
|
|
|
|
|
I0 |
|
|
|||||
|
|
|
ψ 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
δ |
|
|
Ф |
|
ψ 2 |
|
|
|
|
|
δ |
|
|
Ф |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I′ |
|
|
|
|
||
|
|
I′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
U ′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
2 |
|
|
|
|
|
|
|
|
|
U ′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
Е |
|
= Е′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
′ |
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
− I2R2 |
|
|
|
|
|
|
|
|
|
|
Е = |
Е′ |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
− I′R′ |
|
|
|
1 |
|
2 |
|
|
|
|
|
|
− jI2 x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
− jI2 x2 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
а) |
|
|
|
|
|
|
|
|
б) |
|
|
|
|
|
|
|
|
|
Рис.5.7. Векторні діаграми трансформатора: а) індуктивне навантаження; б) ємнісне навантаження
29
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∙ |
|
|
|
|
|
|
1) У масштабі з точки 0 по осі абсцис відкладемо вектор |
∙ |
= |
|
|
|
Е1 |
|
|
. 2) За |
|||||||||||||||||||||||||||||||||||||||
Ф |
|
|
||||||||||||||||||||||||||||||||||||||||||||||
4,44 fw |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
відомим кутом діелектричних утрат |
δ будуємо в масштабі вектор |
|
I0 , |
|||||||||||||||||||||||||||||||||||||||||||||
який випереджає |
|
Ф |
на кут |
δ .3) У вибраному масштабі |
|
|
|
|
відкладаємо |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
. 4) Далі будуємо вектор |
|||||||||||||||||||||
E1 |
та Е2′ , котрі відстають від вектора Ф на 90 |
|
|
|||||||||||||||||||||||||||||||||||||||||||||
струму |
|
1 |
|
|
ψ |
між |
векторами |
|
|
′ |
|
|
|
|
′ |
|
|
визначається |
|
за |
відомим |
|||||||||||||||||||||||||||
I |
2 . Кут |
|
2 |
Е2 |
|
і I 2 |
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
′ |
+ X |
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
навантаженням ψ 2 |
|
= arctg |
|
X2 |
н |
|
. Якщо навантаження індуктивне, то век- |
|||||||||||||||||||||||||||||||||||||||||
|
|
′ |
′ |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
R2 |
+ Rн |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Е′ |
|
|
|
|
|
|
|
|
|
|
′ |
|
|
ψ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
тор |
випереджає вектор |
I |
на кут |
, якщо ємнісне – то вектор |
Е′ |
|||||||||||||||||||||||||||||||||||||||||||
2 |
|
2 |
|
|
|
2 |
|
|
2 |
|||||||||||||||||||||||||||||||||||||||
відстає від вектора |
I 2′ на кут ψ2 . 5) Для знаходження невідомого вектора |
|||||||||||||||||||||||||||||||||||||||||||||||
|
2 |
будуємо векторну суму за рівнянням |
|
|
2 |
= |
|
2 |
− |
|
|
2 |
2 |
|
2 |
|
2 . Для цього з |
|||||||||||||||||||||||||||||||
|
|
|
|
E |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
U ′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U ′ |
|
′ |
jI ′ x |
′ − I ′ R′ |
|
|
|
|
|
|
|
|
||||||||||||||||||
кінця вектора |
|
|
проводимо пряму, перпендикулярну векторові струму |
|||||||||||||||||||||||||||||||||||||||||||||
Е2′ |
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
, і на ній відкладаємо вектор |
− jI |
′ |
|
|
′ |
. Із |
кінця |
вектора |
|
− jI |
′ |
|
′ |
|||||||||||||||||||||||||||||||||
I 2′ |
2 |
X 2 |
|
2 |
X 2 |
|||||||||||||||||||||||||||||||||||||||||||
проводимо пряму, паралельну векторові струму |
|
|
I 2′ , і на ній відкладаємо |
|||||||||||||||||||||||||||||||||||||||||||||
вектор I2′ R2′ . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Зауваження: для того щоб трикутник падіння напруг в обмотках не |
|||||||||||||||||||||||||||||||||||||||||||||||
накладався |
на |
вектори |
|
Е та U , вторинний |
трикутник |
|
напруг краще |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
починати будувати з вектора |
− jI ′ X |
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
2 |
|
2 , а трикутник напруг у первинній |
||||||||||||||||||||||||||||||||||||||||||||||
обмотці |
|
– |
з |
вектора |
|
I1R1 . |
З’єднавши |
кінці |
|
векторів |
|
Е′ |
|
й − I ′ R′ , |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
′ |
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
отримаємо |
вектор |
|
|
і |
трикутник |
|
падіння |
напруг |
|
|
у |
|
вторинному |
|||||||||||||||||||||||||||||||||||
− I2 Z2 |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
ланцюзі. |
|
|
в точку вектора |
− I2 R2 |
проводимо вектор |
U |
2 |
|
|
|
та графічно |
|||||||||||||||||||||||||||||||||||||
Із точки О |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ ′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ϕ |
|
= arctg |
|
X |
′ |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
ϕ |
|
|
|
|
|
|
|
− I ′ |
|
|
|
|U ′ | |
|
|
|
|
|
н |
|
|
|
|
|
|
|
|
|
|||||||||||||
встановлюємо кут |
|
2 |
між векторами |
|
|
2 |
і |
|
|
|
2 |
|
|
; |
|
2 |
|
|
|
|
|
|
|
′ |
. |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Rн |
|
|
|
|
|
|
|
|
||||
|
|
6) Далі визначаємо вектор I1 = I0 |
+ (−I2′ ) . Відкладаємо з кінця вектора |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
вектор |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 , і знаходимо |
|
|
|
0 |
|
|
|
|
|
|
. Інколи |
|||||||||||||||||||||
I 0 |
|
2 , паралельний вектору |
I |
1 |
= I |
+ ( |
2 |
|
||||||||||||||||||||||||||||||||||||||||
|
|
− I ′ |
|
|
|
|
|
|
|
= −I2′ . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I ′ |
|
−I ′ ) |
|
|
|
|
|
||||||||||||||
вектором |
I 0 |
нехтують ,тоді I1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
U |
1 = −Е1 |
+ jI1 X1 |
+ I 2 R2 визначимо вектор |
|
U1 . З кінця |
||||||||||||||||||||||||||||||||||
|
|
7) За рівнянням |
|
|||||||||||||||||||||||||||||||||||||||||||||
вектора |
−Е1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
відкладаємо вектор I1R1 , паралельний вектору I1 ; з кінця |
||||||||||||||||||||||||||||||||||||||||||||||||
вектора |
|
|
|
|
|
|
прямій, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
векторові |
|
|
|
|
|
|
I1 , |
||||||||||||||||
|
I1R1 , на |
перпендикулярній |
|
|
струму |
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
jI1 X1 . З’єднавши |
|
кінці |
векторів |
|
−Е1 |
та |
|
|
|
|
|
|||||||||||||||||||||||||||||
відкладаємо |
вектор |
|
|
|
|
jI1 X 1 , |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
отримаємо трикутник падіння напруг у первинній обмотці і вектор I1Z1 . |
||||||||||||||||||||||||||||||||||||||||||||||||
З’єднавши точку О та кінець вектора |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U1 |
|||||||||||||||||
I1Z1 , одержимо шуканий вектор |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
і кут ϕ1 між векторами |
|
|
та |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
U1 |
I1 . При значному ємнісному навантаженні |
|||||||||||||||||||||||||||||||||||||||||||||||
напруга |
U 2 |
трансформатора перевищує ЕРС |
Е2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6.Трифазні трансформатори
6.1. Будова трифазних трансформаторів
30
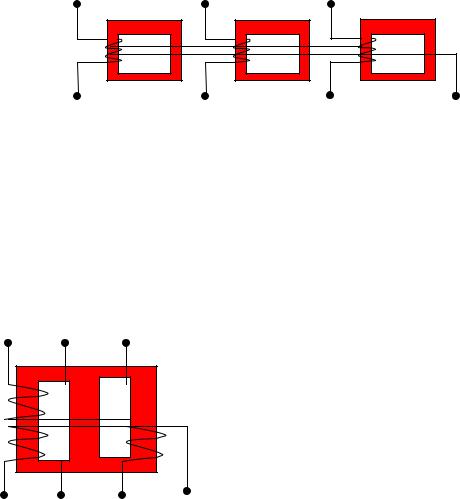
Перетворення трифазної системи напруг можливо виконати трьома однофазними трансформаторами, які утворюють трансформаторну групу (рис.6.1).
А |
В |
С |
|
Х |
У |
|
Z |
x |
y |
|
z |
a |
в |
с |
0 |
Рис. 6.1. Трансформаторна група трифазної мережі Початки
первинних фазних обмоток позначають великими літерами А, B, C, а початки вторинних обмоток малими a, b, c; кінці обмоток відповідно X, Y, Z та x, y, z.
Недоліки трансформаторних груп – великий розмір, значна вага, велика вартість.
А В С
ХУ Z
Z
ху  z
z
а |
в |
с |
0 |
|
Рис. 6.2. Трифазний трансформатор
Тому в установках потужністю до 60000 кВА
використовують трифазні трансформатори, в яких обмотки розташовані на трьох стрижнях, з’єднаних у загальний магнітопровід двома ярмами (рис. 6.2). Отриманий магнітопровід є несиметричним, тобто магнітний опір потоку середньої фази ФВ менше від магнітного опору потоку фаз ФА і ФС . Тому при подачі на вхід трансформатора симетричної системи напруги намагнічуючі струми у фазах утворять несимет-
31
|
|
|
|
|
|
|
|
|
|
ричну |
систему |
струмів, |
|
оскільки |
|
|
|
iB |
> ia , |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
iB > iC |
(рис. 6.3). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
а) |
|
|
|
|
|
|
б) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис.6.3. Несиметричні системи потоків (а) та струмів (б) трифазного |
|
|||||||||||||||||||||||||||
|
Позначення та співвідношення |
|
|
Позначення та співвідношення |
|
|
||||||||||||||||||||||||
|
|
трансформатора |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
електростатики |
|
|
|
|
|
магнітостатики |
|
|
|
|
|
|
|
|
|||||||||||||
Електричний потік (струм) – |
I |
[А] |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
Для зменшення різниці магнітного опору використовують такі засоби: |
|
|
|
||||||||||||||||||||||||||
Напруженість електричного |
|
|
|
Магнітний потік – |
Ф |
|
[Вб] |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
- збільшують поперечний розріз ярма на 10-15%; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
é |
В ù |
|
|
|
|
|
|
|
Напруженість магнітного поля – |
|
|
|
|
|
|||||||||||||
|
- ярмо роблять не прямим, а у формі рівностороннього трикутника, тобто |
|
||||||||||||||||||||||||||||
поля – ε |
ê |
ú |
|
|
|
|
|
|
|
é |
А ù |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
ë |
м û |
|
|
|
|
|
|
|
H ê |
ú |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
обмотки трансформатора виконуються на ребрах правильної трикутної |
|
||||||||||||||||||||||||||||
Електрична напруга – U [В] |
|
|
|
ë |
м û |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
Магнітна напруга – F[A] |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
призми. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Електричний опір провідника – R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
|
|
|||||||||||
|
|
Розглянемо питання, як змінюється намагнічуючий струмR |
і |
|
||||||||||||||||||||||||||
Електричний |
струм |
(потік) |
у |
Магнітний опір провідника – |
|
|
m |
|
|
|
|
|
||||||||||||||||||
|
магнітний потік |
Ф |
|
у замкнутому контурі (р с.6.4, а), якщо магнітний опір |
|
|||||||||||||||||||||||||
електричному колі (закон Ома) |
|
|
Магнітний |
потік у магнітному полі |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
δ |
при |
|
незмінній |
|
|||||||||||||||||||||
|
збільшити |
шляхом уведення повітряного проміжку |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
I = |
U |
|
|
|
|
|
|
|
|
|
|
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
напрузі живлення магнітопроводу (рис.6.4, б). |
I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(6.1) |
||||||||||||
|
|
|
I |
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
δ |
|
|
|
|
||||||
Електрична напруга |
електричному |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Магнітна напруга |
|
|
|
|
|
|
|
|
|
|
полі |
|
|
|||||||||||||||||
полі |
U1 |
|
|
|
|
|
Ф |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
U |
|
|
|
|
|
|
U1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
× |
|
Ф |
|
|
|
|
|
(6.2) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
де l |
– довжина провідника, |
|
|
|
де l |
– довжина магнітного провідника |
|
|||||||||||||||||||||||
|
|
|
|
|
|
а) |
ù |
|
|
|
(магнітопроводу) |
|
|
б) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
щільність струму J ê |
|
2 ú |
|
|
|
|
|
|
|
|
|
|
|
|
é |
Вб |
|
|
|
ù |
|
|
||||||||
|
|
|
Рис. 6.4. Замкнений (а) та розімкнений магнітний контур (б) |
= Тлú |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
ë |
|
û |
|
|
|
Індукція магнітного поля |
|
B |
ê |
м |
2 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ë |
|
|
|
|
|
û |
|
|
|
|
|
|
|
|
I = J ×Q |
|
|
|
|
|
|
|
|
|
|
Ф = В ×Q , |
|
|
|
|
|
|
(6.3) |
|||||||
|
|
Для цього скористаємося глибокою аналогією, яка існує між елект- |
|
|||||||||||||||||||||||||||
|
Q |
|
|
|
|
|
, |
|
|
|
|
де Q – площа поперечного перерізу |
|
|
||||||||||||||||
де |
ростатичним та маг ітними полями, при цьому для зручності порівняння з |
|
||||||||||||||||||||||||||||
|
– площа |
поперечного перерізу |
магнітопроводу |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
лівої сторони сторінки записані відомі закони електростатики, а з правої |
|
||||||||||||||||||||||||||||
провідника |
|
|
|
|
|
|
|
|
|
|
|
|
|
B = μ × H , |
|
|
|
|
|
|
(6.4) |
|||||||||
|
–аналогічні їм закони магнітостатики. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
J = g ×ε |
|
, |
|
|
|
де μ = μ0 × μr |
– магнітна проникливість |
|
|
|||||||||||||||||
де g – питома електрична |
|
|
|
магнітопроводу; μ0 = |
4 ×π ×10 |
7 |
é Гн |
ù |
|
– магнітна |
||||||||||||||||||||
|
|
провідність провідника |
|
|
|
ê |
м |
ú |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ë |
û |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
стала вакууму; μr |
– відносна магнітна |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
проникливість магнітопроводу |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Питомий магнітний опір |
|
= 1 |
|
|
|
|
|
|
|
|
||||||||
Питомий електричний опір |
|
|
|
|
|
|
|
|
ρ |
м |
|
|
|
|
|
|
|
(6.5) |
||||||||||||
|
|
|
32 |
|
|
|
|
|
|
|
μ |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ρ = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
g |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Електричний опір провідника |
Магнітний опір провідника |
|
||||||||||||||||
R = ρ × |
l |
= |
l |
|
|
|
|
Rm = ρм |
× |
l |
= |
l |
|
|
(6.6) |
|||
|
g ×Q |
|
|
|
|
μ ×Q |
||||||||||||
|
Q |
|
|
|
|
|
|
|
Q |
|
||||||||
Співвідношення для магнітного опору (6.6) отримуємо послідовним |
|
|||||||||||||||||
використанням формул (6.3), (6.4), (6.2) |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
Ф = В × Q = μ × H × Q = μ × Q × |
F |
= |
|
F |
|
|
|
|
|
|||||
|
|
|
|
|
l . |
|
(6.7) |
|
||||||||||
|
|
|
|
|
|
|
|
|
l |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
μ × Q |
|
|
|
|
|
||
Порівнюючи одержаний магнітний потік (6.7) із (6.1), отримуємо |
|
|||||||||||||||||
формулу для магнітного опору магнітопроводу(6.6). |
|
|
|
|
||||||||||||||
Отже, при зростанні δ довжина |
магнітопроводу |
l |
збільшується й |
|||||||||||||||
магнітний опір магнітопроводу |
Rm |
також підвищується. Магнітний потік |
||||||||||||||||
визначається із (4.17) і дорівнює |
Е |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
Ф = |
|
. |
|
|
|
|
|
(6.8) |
|||||
|
|
|
|
|
4,44wf |
|
|
|
|
|
||||||||
33

Оскільки E ≈ U = const , частота f та кількість витків обмотки не змінюються, то магнітний потік Ф не залежить від величини проміжку δ і залишається постійним.
Якщо взяти до уваги, що магнітна напруга або магніторушійна сила
F обмотки обчислюється за формулою |
|
F = 2 × I ×W , |
(6.9) |
то тоді магнітний потік у магнітопроводі згідно з (6.1) визначається формулою
Ф = |
F |
= |
|
2 |
× I ×W |
. |
(6.10) |
|
|
|
|
||||
|
Rm |
|
Rm |
|
|||
Із (6.10) видно, що магнітний потік Ф при збільшенні проміжку δ |
|||||||
(тобто Rm ) може залишатися постійним, якщо струм I |
буде також |
||||||
зростати. Отже, при збільшенні повітряного проміжку δ магнітний потік залишається незмінним, а струм I зростає.
Тому струм ХХ у двигунах більше, ніж струм ХХ у трансформаторах, оскільки у них більший повітряний проміжок δ у магнітному колі.
6.2. Явища при намагнічуванні трансформатора
Розглянемо глибше процес намагнічування трансформатора. Нехай до обмотки трифазного трансформатора підведена симетрична система напруг. При цьому магнітний потік буде також симетричним і матиме синусоїдальну форму Ф = Фm sinωt . Але у випадку явища насичення осердя струм в обмотках буде мати несинусоїдальну форму. Знайти форму струму намагнічування можна графічно, по відомих кривих намагнічування і магнітного потоку (рис.6.5).
34
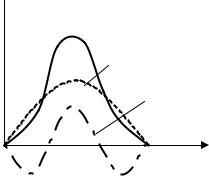
Рис.6.5. Графічна побудова кривої струму намагнічування
На рисунку 6.5 в лівому верхньому квадранті показана синусоїдальна крива магнітного потоку Ф = Фm sin ωt , а в правому верхньому квадранті – крива намагнічування матеріалу осердя. Для отримання кривої розбивають криву на ряд ділянок (у нашому випадкові на 6), проектують їх на криву намагнічування та визначають відповідні намагнічуючі струми I.
 І
І
I(t)
I1(t)
I3(t)
t
Рис. 6.6. Форма струму намагнічування
Потім проводять із вибраних крапок перпендикуляри на вісь t і знаходять відповідні моменти часу t1 , t2 , t3 , t4 ,t5, t6.
У місцях перемикань у правому нижньому квадранті отримують крапки кривої намагнічування струму I (t ) . Як видно, крива струму має несинусоїдальну форму (рис.6.6).
35
Якщо несинусоїдальну криву намагнічування розкласти в ряд Фур’є, то струм буде мати непарні гармоніки 1,3,5,7 і т.д. Векторне рівняння струму
|
|
|
I = I1 + I3 + I5 + I7 . |
|
|
(6.11) |
|||||
Діюче значення намагнічуючого струму |
|
|
|
||||||||
|
I = |
|
I 21 + I 23 + I 25 |
+ I 27 |
= I1 |
1+ α 2 + β 2 + γ 2 |
= К∂ I1 , |
(6.12) |
|||
де α, β,γ – |
коефіцієнти відносного вмісту струмів |
вищих |
гармонік |
||||||||
стосовно першої; К ∂ – |
коефіцієнт |
відносного |
вмісту |
вищих |
гармонік |
||||||
стосовно першої гармоніки |
|
|
|
|
|
|
|
(6.13) |
|||
|
I3 =αI1; |
I5 = βI1; I7 = γI1; |
|
|
|||||||
|
|
|
Kд = |
|
.... |
|
|
(6.14) |
|||
|
|
|
1+α 2 + β 2 + γ 2 + |
|
|
||||||
Значення коефіцієнтів α, β і Кд |
залежить від амплітуди магнітного |
||||||||||
потоку Bm . |
|
|
|
|
|
|
|
|
|
|
|
У таблиці 6.1 наведені дані для холоднокатаних сталей. |
|
||||||||||
|
Параметри холоднокатаних сталей |
Таблиця 6.1 |
|||||||||
|
|
|
|||||||||
Вm , Тл |
1,0 |
1,2 |
|
1,4 |
|
|
|
1,6 |
1,8 |
2,0 |
|
α |
0,21 |
0,23 |
|
0,28 |
|
|
0,34 |
0,48 |
0,69 |
||
β |
0,05 |
0,08 |
|
0,12 |
|
|
0,18 |
0,24 |
0,36 |
||
K д |
1,02 |
1,03 |
|
1,04 |
|
|
1,07 |
1,14 |
1,27 |
||
Тобто при індукції Вm ≤1,6 Тл можна вважати, що I ≈ I1 .
6.3. З’єднання обмоток трансформаторів
Фазні обмотки трифазних трансформаторів можуть з’єднувати “зіркою” – таблиця 6.2, а, “трикутником” – таблиця 6.2, б та “зигзагом” –таблиця 6.2, в.
1  з’єднанняВид
з’єднанняВид 
Види з’єднань обмоток трансформаторів |
Таблиця 6.2 |
||
|
|||
2 |
3 |
4 |
5 |
|
|
Співвідношення |
|
Графічне |
Умовне |
фазних (UA) та |
Векторні |
зображення |
позначення |
лінійних (UAB) |
діаграми |
|
|
напруг |
|
36
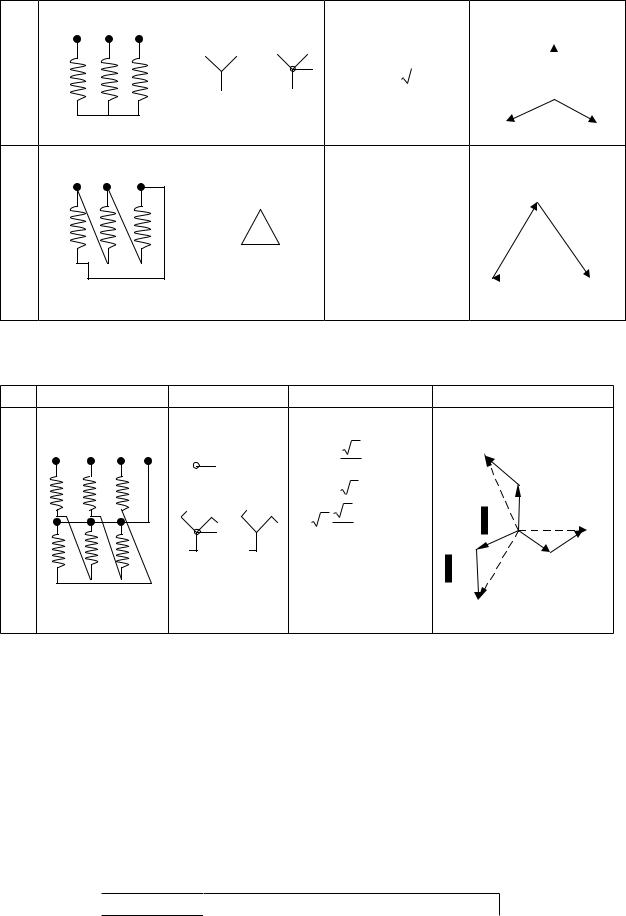
АВ С
а) |
|
|
X |
Y |
Z |
А |
В |
С |
б) |
|
|
X |
Y |
Z |
|
|
|
|
|
|
В |
|
|
||
U AB = |
|
|
U A |
|
|
Ф |
|
|
|
|
|
|
|
|
|
|
|
||||
|
3 |
|
|
А |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А |
|
|
|
|
С |
|
|
|
|
|
А |
|
|
|
|
Ф |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
В |
|
В |
||
|
|
|
|
|
|
|
Ф |
|||
U AB |
=U A |
|
|
|
|
|
|
|||
UAB |
|
|
U |
|
А |
|||||
|
|
|
|
|
|
|
|
|
BC |
|
|
|
|
|
|
|
|
|
|
|
С |
|
|
|
|
А |
UCA |
|
||||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
Продовження таблиці 6.2 |
|||
1 |
2 |
|
|
3 |
|
|
4 |
|
|
|
5 |
|
А |
В |
С 0 |
Z |
Z |
UФА = |
3 |
U A |
|
В |
|
|
|
|
|
|
2 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
U AB = |
3UФA = |
|
|
|
|||
|
|
|
|
|
|
3 U A = |
3 U A |
|
1 |
|
||
в) |
|
|
|
|
= 3 |
|
2U A |
С |
||||
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 U A |
|
UФА |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
X |
Y |
Z |
|
|
|
|
|
|
|
А |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Схеми з’єднань трифазних трансформаторів зазначають дробом: у чисельнику з’єднання обмоток ВН, у знаменнику – з’єднання обмотки НН, наприклад, Y / Y , Y / , Y / Z .
Лінійний коефіцієнт трансформації дорівнює відношенню лінійних ЕРС, а відношення фазних ЕРС – це фазний коефіцієнт трансформації
|
Е |
|
|
Е |
W |
|
||
К Л = |
1 |
; |
КФ = |
1Ф |
= |
1 |
. |
(6.15) |
Е2 |
|
|
||||||
|
|
|
Е2Ф |
W2 |
|
|||
Співвідношення між лінійними та фазними коефіцієнтами трансформації наведені у таблиці 6.3.
Таблиця 6.3 Лінійні та фазні коефіцієнти трансформації  З’єднання
З’єднання  Зв’язок між лінійними та фазними
Зв’язок між лінійними та фазними
37
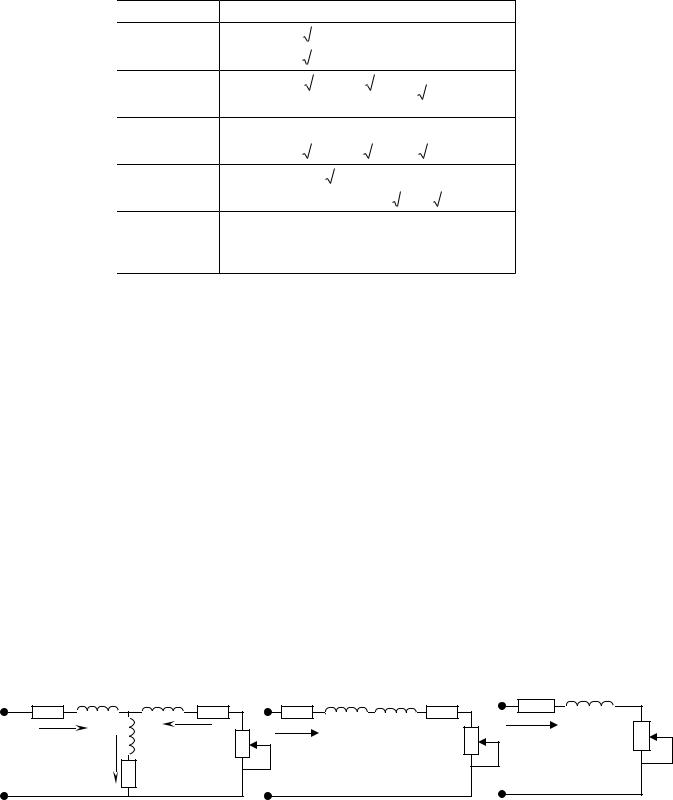
обмоток |
коефіцієнтами трансформації |
|
|||||||||||||||||||||||||||||||||||||||||||||
Y / Y , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
К л = |
|
Е1 |
= |
|
|
|
3 |
Е1Ф |
= |
|
w1 |
|
|
= Кф |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
/ ,Z / Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
Е2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
3Е2Ф |
|
|
w2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Y / |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Е1 |
|
|
|
|
|
3Е1Ф |
|
|
|
|
|
|
3w1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
К л = |
|
= |
|
|
|
|
= |
|
|
|
= 3Кф |
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
Е2Ф |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
Е2 |
|
|
|
|
|
|
|
|
|
|
w2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(6.16) |
|||||||||||||||
/ Y |
|
|
|
|
Е |
|
|
|
|
|
|
Е |
|
|
|
|
|
|
|
|
|
w |
|
|
|
|
|
|
|
Кф |
|||||||||||||||||
К л = |
|
|
= |
|
|
|
|
|
|
|
|
= |
|
|
|
|
= |
|
|
||||||||||||||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
1Ф |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
Е2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
3Е2Ф |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3w2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Y / Z |
|
|
|
|
Е |
|
Е |
|
|
|
|
|
|
|
|
w |
2 |
|
|
|
|
|
2Кф |
|
|||||||||||||||||||||||
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
К л = |
|
|
1 |
|
= |
|
|
|
1Ф |
|
|
|
|
|
= |
|
|
1 |
× |
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
Е2 |
|
Е2Ф 3/ 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
3 |
|
|
3 |
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
w2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
/ Z |
К л = |
|
|
Е |
= |
|
|
Е |
|
= |
|
w |
= |
2Кф |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
1 |
|
|
|
|
|
1Ф |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
3 |
|
|
|
|
w2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
Е2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 Е2Ф |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Зазначимо, що на практиці у трифазних трансформаторах завжди використовують лінійні коефіцієнти трансформації К Л , оскільки їх зручніше вимірювати, причому в позначенні індекс Л опускають.
7.Робота трансформатора під навантаженням
7.1.Спрощена векторна діаграма
На практиці для трансформаторів середніх та великих потужностей використовують спрощену схему заміщення і спрощену векторну діаграму трансформатора.
Для таких трансформаторів струм ХХ I0 становить 0,6-3%, і ним нехтують, тобто I0 = 0.
Первинна мережа живлення при цьому вважається нескінченно великої потужності й зміни напруги на первинній обмотці немає, тобто U1 = const при довільних навантаженнях. Еквівалентна схема при цьому змінюється так (рис.7.1).
R1 |
X1 |
X'2 |
|
R'2 |
|
I1 |
I0 |
Xm |
I'2 |
Z' |
н |
|
Rm |
|
|
||
|
|
|
|
||
|
|
|
H |
|
|
|
|
а) |
|
|
|
R1 |
X1 |
X'2 |
R'2 |
Rk |
Xk |
I1 |
|
|
Z'H |
I1=I1H= -I’2 |
Z'H |
|
|
|
|
== |
|
|
|
б) |
|
U1 |
|
Рис. 7.1. Спрощення схеми заміщення потужних трансформаторів: а) вихідна схема заміщення; б) спрощена схема ( I0 = 0 );
в) результуюча схема заміщення
38
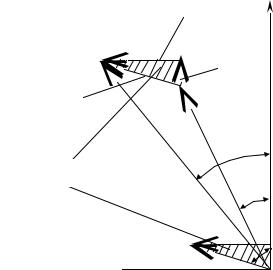
У спрощеній схемі прийняті позначення
|
|
Rk = R1 + |
|
' |
X k |
= X1 + X |
' |
; |
|
|
|
|
|
|
|
, |
(7.1) |
||||||||
|
|
R2 ; |
2 |
Zk = Rk + jX k |
|||||||||||||||||||||
де |
Rk , X k |
– це опір трикутника КЗ, оскільки |
|
I1 = I1H (як і в досліді КЗ, |
|||||||||||||||||||||
рис.5.4). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для спрощеної схеми трансформатора можна записати рівняння |
||||||||||||||||||||||||
напруг |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 . |
(7.2) |
|
|
|
1 |
k |
|
2 |
|
k |
2 |
|
|
|
k |
|
|
k |
||||||||||
|
|
U |
= U |
|
|
1 |
Z |
+ U |
= |
|
1 |
R |
+ |
1 |
X |
+ U |
|||||||||
|
|
|
|
+ U ′ |
= I |
|
′ |
I |
|
jI |
|
′ |
|
||||||||||||
|
У |
цьому векторному |
|
рівнянні, |
|
|
|
якщо |
|
|
відомі |
величини |
|||||||||||||
' |
|
,U ka = I1 Rka ,U kp = I1 X k , cosϕk , |
|
то |
|
потрібно |
|
|
графічно знайти |
||||||||||||||||
U 2 |
, I1 , cosϕ2 |
|
|
|
|
||||||||||||||||||||
U1 , cosϕ1 . Це можна зробити за допомогою спрощеної векторної діаграми, яка будується так (рис.7.2).
|
I1Xk |
=Ukр |
|
I |
|
= −I |
` |
||
|
I |
R |
=U |
|
1 |
2 |
|||
|
ka |
|
|||||||
|
|
1 |
k |
|
|
|
|
||
|
|
|
|
′ |
|
|
|
|
|
I1Zk =Uk |
|
U |
2 |
|
|
|
|
|
|
|
|
|
ϕ1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Трикутник |
U1 |
|
|
ϕ 2 |
|
|
|
|
|
КЗ |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
ϕ k |
|
||
Рис. 7.2. Спрощена векторна діаграма: |
|
||||||||
– активна та реактивна складові |
|
|
|
|
|||||
трикутника КЗ |
|
|
|
|
|
|
|
|
|
1) На осі ординат у вибраному масштабі будують
вектор |
струму I1 = −I2′ . |
2) |
|
Потім |
під кутом |
2 |
у |
|
|
ϕ |
|
масштабі відкладають вектор
U2′ .
3) Паралельно вектору І1 із
кінця |
вектора |
U ka |
U 2' |
відкладають вектор |
= I1 Rk |
||
|
|
|
|
.
39
|
|
|
4) |
З |
кінця вектора |
|
|||
|
|
|
U ka |
||||||
|
|
|
перпендикулярно |
векторові |
|||||
|
|
|
струму |
|
проводять вектор |
||||
|
|
|
I1 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Ukp = I1 X k . |
|
|
|
|
||
5) Замикаючи кінець вектора |
|
' |
та кінець |
вектора |
|
|
отримаємо |
||
|
U |
kp , |
|||||||
U 2 |
|
||||||||
трикутник короткого замикання (КЗ). Замикаючи кінець вектора Ukp і точку О, одержимо графічно вектор U1 та значення cosϕ1 .
Більш цікавий для практики випадок полягає в тому, що за відомими
значеннями |
U1 |
, I1 , cosϕ2 і трикутником КЗ, тобто Rk, Xk, потрібно |
|||||
|
|
|
|
|
|
|
|
графічно знайти |
|
2 |
|
1 |
. Цю задачу можна розв’язати так: |
||
|
|||||||
|
|
U ′ |
|
,cos ϕ |
|
||
1) По осі Y відкладаємо у масштабі
Рис. 7.3. Знаходження U2 та за спрощеною діаграмою
вектор струму I1 та будуємо з початку координат трикутник напруг КЗ.
2) З початку координат проводимо
|
дугу радіусом |
|
|
|
. |
|
||
|
|
|
|
|||||
|
|
U 1 |
|
|
||||
|
3) Переміщуючи трикутник КЗ па- |
|||||||
|
ралельно вздовж вектора U2′ , |
|
||||||
|
|
|
|
|
|
|
|
у точці |
суміщуємо кінець трикутника КЗ із дугою, описаною вектором U 1 |
||||||||
С. |
|
|
та cosϕ |
|
||||
|
|
|
||||||
4) Графічно визначаємо невідомі |
U ′ |
|
|
|||||
2 |
|
1 . |
|
|
|
|
|
|
Тепер, виходячи зі спрощеної векторної діаграми трансформатора, знайдемо аналітичне рівняння векторної характеристики трансформатора, тобто залежність U 2 ( I2 ).
7.2. Зовнішня характеристика трансформатора
Залежність вторинної напруги трансформатора від струму навантаження U2 (I2 ) називається зовнішньою характеристикою трансформатора.
40
