2.2. Визначення максимального потоку в мережах поштового зв’язку.

Поштовий потік – число поштових відправлень одного виду, які слідують в певному напрямку.

Характерними властивостями поштових потоків є їх нерівномірність у часі та по напрямкам.

Причини нерівномірності поштових потоків:

- нерівномірність прийому кореспонденції від населення та підприємств по годинах в добі;

- нерівномірність в русі магістрального та місцевого транспорту;

- нерівномірність надходження періодичних видань по годинах в добі та тижням місяця;

- сезонні коливання попиту на послуги поштового зв’язку (різні товари і продукти, святкові потоки).

Розглянемо алгоритм визначення максимального потоку в мережі поштового зв’язку.

Для знаходження максимального потоку в мережах поштового зв’язку прийнято використовувати методи теорії графів. В цьому випадку мережа поштового зв’язку представляється у вигляді графа вершинам якого відповідають відділення поштового зв’язку, а ребрам – пропускна здатність шляхів між вершинами графу (найчастіше – вантажопідйомність транспортних засобів, що використовуються для перевезення поштових відправлень).

Кожній дузі графа (х,у) протиставимо число f(x,y), яке називається пропускною здатністю. Виділимо виток s і стік t. Функція φ(х,у) має назву потоку на графі, якщо вона відповідає наступним умовам:

1. φ(х,у)≥0

2. Для будь-якої вершини х, що не є витоком або стоком, сумарний вхідний потік дорівнює сумарному вихідному потоку, тобто:

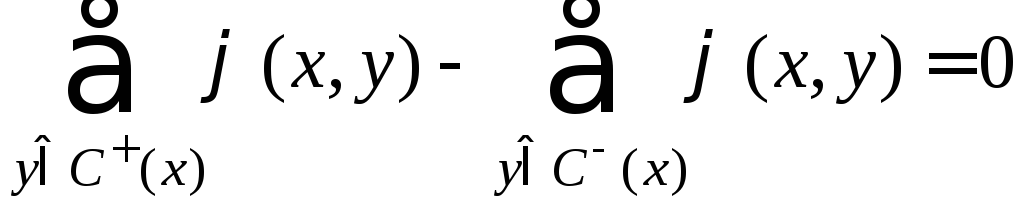
3. φ(х, у)≤ f(x, y).

Величиною потоку називається сума потоків за всіма дугами, що виходять з витоку s, або:

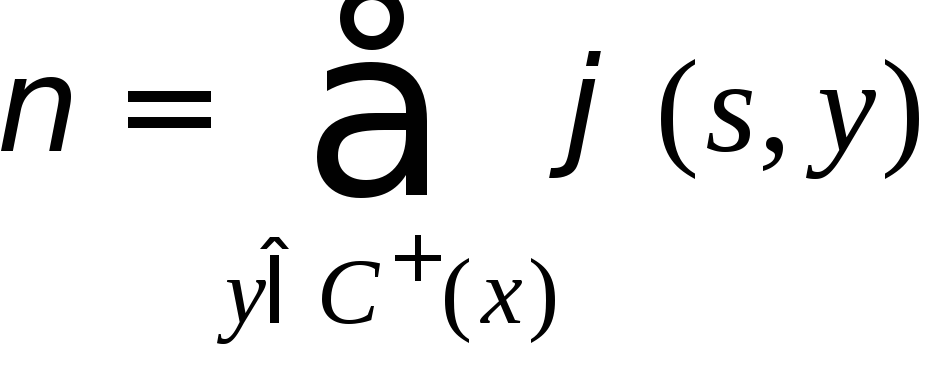
Теорема про максимальний потік формулюється так:

для заданої мережі максимальна величина потоку дорівнює мінімальній пропускній здатності перерізу.

Приклад визначення максимального потоку в мережі поштового зв’язку.

Розглянемо граф G(X,Y), вершини якого відповідають вузлам мережі перевезень пошти, ребра – поштовим маршрутам, що з’єднують вузли мережі, а ваги ребер – їх пропускним здатностям.

Рис.1 Приклад графа мережі поштового зв'язку

Пропускна здатність ребра дорівнює сумі пропускних здатностей (вантажопідйомності) транспортних одиниць усіх поштових маршрутів, що прямують по зазначеному ребру.

У мережі поштового зв'язку, яку відображає граф, для перевезень пошти використовуються маршрути:

М1: 1 – 2 – 3 – 4 – 5; М2: 5 – 4 – 3 – 2 – 1, пропускна здатність R(М1)=R(М2)=1

М3: 1 – 4; М4: 4 – 1, пропускна здатність R(М3)=R(М4)=5

М5: 2 – 3 – 5; М6: 5 – 3 – 2, пропускна здатність R(М5)=R(М6)=3

М7: 3 – 5; М8: 5 – 3, пропускна здатність R(М7)=R(М8)=3

Загальний вигляд матриці пропускних здатностей ребер граф

Вершина	1	2	3	4	5
1	Р(1,1)	Р(1,2)	Р(1,3)	Р(1,4)	Р(1,5)
2	Р(2,1)	Р(2,2)	Р(2,3)	Р(2,4)	Р(2,5)
3	Р(3,1)	Р(3,2)	Р(3,3)	Р(3,4)	Р(3,5)
4	Р(4,1)	Р(4,2)	Р(4,3)	Р(4,4)	Р(4,5)
5	Р(5,1)	Р(5,2)	Р(5,3)	Р(5,4)	Р(5,5)

Матриця пропускних здатностей ребер графа рис.2

Вершина	1	2	3	4	5
1	–	1	0	5	0
2	1	–	4	0	0
3	0	4	–	1	6
4	5	0	1	–	1
5	0	0	6	1	–

Для з'ясування значень максимальних потоків між вузлами мережі перевезень пошти використовуються значення перетинів (перерізів) графа.

Перетином (перерізом) зв'язного графа G(X, Y) називається не надмірна множина його дуг (ребер), вилучення яких розділяє зазначений граф на два незв'язаних між собою підграфа G₁(X₁, Y₁) і G₂(X₂, Y₂) .

Пропускна здатність перерізу дорівнює сумі пропускних здатностей дуг (ребер), що його створюють.

Відповідно до однієї з основних теорем теорії графів величина максимального потоку між вершинами і та j графа дорівнює мінімальній величині пропускної спроможності перетину, що розділяє зазначені вершини.

Розглядаючи послідовно всі перетини, що розділяють вершини і та j, можна визначити з них те, яке має мінімальну пропускну спроможність, і, тим самим, визначити величину максимального потоку між зазначеними вершинами.

Будемо вважати, що кожен перетин заданий n-розрядним двійковим кодом, в якому вершинам-витокам відповідають одиниці, а вершинам-стокам – нулі. Наприклад, перетин, що розділяє вершини 1, 3, 5 і 2, 4 має код 10101.

Оскільки загальне число n-розрядних двійкових кодів складає 2ⁿ, а коди 00 … 0 і 11 … 1 не є кодами перетинів, існує 2ⁿ - 2 перетинів орієнтованого і 2^n-1 - 1 перетинів неорієнтованого графа. Таким чином, послідовність кодів перетинів відповідає послідовності звичайних двійкових кодів.

Крок 1 R (00001)=(11110)=

Крок 2 R (00010)=(11101)=

Крок 3 R (00011)=(11100)=

Крок 4 R (00100)=(11011)=

Крок 5 R (00101)=(11010)=

Крок 6 R (00110)=(11001)=

Крок 7 R (00111)=(11000)=

Крок 8 R (01000)=(10111)=

Крок 9 R (01001)=(10110)=

Крок 10 R (01010)=(10101)=

Крок 11 R (01011)=(10100)=

Крок 12 R (01100)=(10011)=

Крок 13 R (01101)=(10010)=

Крок 14 R (01110)=(10001)=

Крок 15 R (01111)=(10000)=

Початкові величини максимальних потоків між усіма парами вершин графа подаються у вигляді матриці і приймаються необмеженими.

Створюється код чергового перетину і обчислюється величина його пропускної здатності, яка порівнюється з раніше отриманими величинами всіх потоків, що розділяються зазначеним перетином.

Якщо обчислена величина пропускної здатності перетину менше, ніж величина відповідного потоку, остання замінюється першою.

Після розглядання всіх перетинів графа автоматично створюється матриця величин максимальних потоків між усіма парами вершин графа, тобто, між усіма парами вузлів мережі перевезень пошти.

Приклад

Крок 0: початковий							Крок 1: R(00001) = R(11110) = 7
Вершина	1	2	3	4	5		Вершина	1	2	3	4	5
1	-	999	999	999	999		1	-	999	999	999	7
2	999	-	999	999	999		2	999	-	999	999	7
3	999	999	-	999	999		3	999	999	-	999	7
4	999	999	999	-	999		4	999	999	999	-	7
5	999	999	999	999	-		5	7	7	7	7	-

Крок 5: R(00101) = R(11010) = 6							Крок 8: R(01000) = R(10111) = 5
Вершина	1	2	3	4	5		Вершина	1	2	3	4	5
1	-	999	6	7	6		1	-	5	6	7	6
2	999	-	6	7	6		2	5	-	5	5	5
3	6	6	-	6	7		3	6	5	-	6	7
4	7	7	6	-	6		4	7	5	6	-	6
5	6	6	7	6	-		5	6	5	7	6	-

Крок 13: R(01101) = R(10010) = 3							Крок 15: R(01111) = R(10000) = 6
Вершина	1	2	3	4	5		Вершина	1	2	3	4	5
1	-	3	3	7	3		1	-	3	3	6	3
2	3	-	5	3	5		2	3	-	5	3	5
3	3	5	-	3	7		3	3	5	-	3	7
4	7	3	3	-	3		4	6	3	3	-	3
5	3	5	7	3	-		5	3	5	7	3	-

При визначенні шляхів передачі максимальних потоків між вузлами мережі перевезень пошти потрібно враховувати, що наявність прямого маршруту між вузлами і та j не означає його обов'язкового використання.

Так, у відповідності до розглянутого прикладу, максимальний потік між вузлами 1 і 5 становить 3. У перетин з мінімальною пропускною здатністю, що розділяє вузли 1 і 5, входять ребра (1,2), (3,4), (4,5).

Якщо для передачі максимального потоку використати прямий маршрут М1: 1 – 2 – 3 – 4 – 5 із пропускною здатністю 1, він займе всі зазначені ребра і, тим самим, перекриє інші шляхи його передачі.

Передача максимального потоку буде забезпечена, якщо для цього використати комбіновані маршрути: М1, М5: 1 – 2 – 3 – 5 з пропускною здатністю1; М3, М2, М5: 1 – 4 – 3 – 5 з пропускною здатністю 1; М3, М1 1 – 4 – 5 з пропускною здатністю 1.