2 Методичні вказівки до виконання розрахунковографічної роботи та варіанти завдань

Метою виконання розрахунково-графічної роботи є перевірка ступеня засвоєння усіх змістових модулів дисципліни «Основи поштового зв’язку». Робота складається з трьох завдань. Перше завдання – визначення найкоротших маршрутів між вузлами перевезень пошти, друге завдання – визначення максимальних потоків в мережі поштового зв’язку, третє завдання – складання оптимального маршруту перевезень поштових відправлень. Номер варіанту завдання співпадає з номером по списку в журналі студента.

Звіт про виконану розрахунково-графічну роботу має бути оформлений на стандартних аркушах формату А4 у тестовому редакторі MS Word (або Open Office.org Writer) та своєчасно поданий на перевірку викладачеві.

2.1. Алгоритм Флойда для знаходження найкоротших маршрутів перевезень пошти.

Для знаходження найкоротших маршрутів перевезень пошти, мережу потового зв’язку представляють у вигляді графа. Вершини цього графа відповідають відділенням поштового зв’язку, а ребра – відстаням між ними. Найбільш розповсюдженим та точним алгоритмом, що дозволяє вирішити подібну задачу оптимізації методами теорії графів є алгоритм Флойда.

Алгоритм Флойда застосовується для довільних, в тому числі і від'ємних довжин ребер (випадок наявності циклів від'ємної довжини треба виключити). Він дає змогу знайти найкоротші шляхи між всіма парами вершин графа.

Метод заснований на послідовному перетворенні матриці С, в якій з самого початку записані довжини всіх дуг графа. У випадку неорієнтованого ребра йому ставиться у відповідність дві дуги.

Опис алгоритму:

1. Сформувати матрицю С , елемент якої:

Покладемо k=1.

2. Для всіх здійснити операцію.

3. Якщо, то в графі існує цикл від'ємної довжини, який має вершину . Розв'язок необмежений. У протилежному випадку перейти до кроку 4.

4. Якщо , обчислення закінчені, розв'язок знайдено. Якщо ні, перейти до кроку 5.

5. Прийняти , перейти до кроку 2.

Якщо довжини всіх дуг невід'ємні, то крок 3 можна виключити.

Структурна схема алгоритму Флойда зображена на рис. 3.

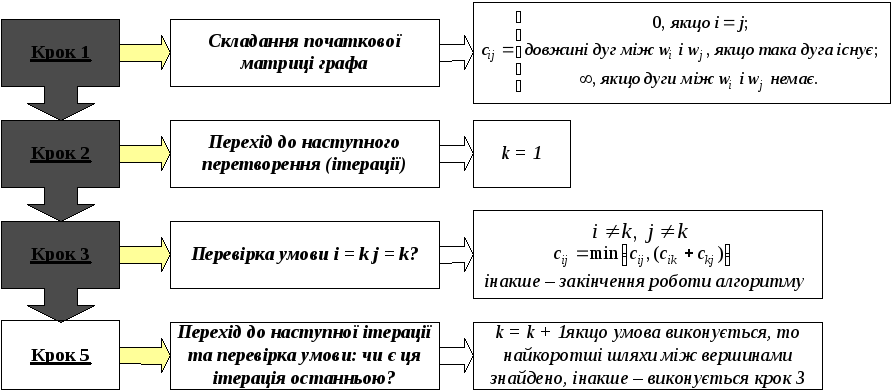
Рисунок 1 – Спрощена блок-схема роботи алгоритму Флойда

Розглянемо приклад.

Для графа, зображеного на рис.2 . знайти найкоротші шляхи між усіма вузлами.

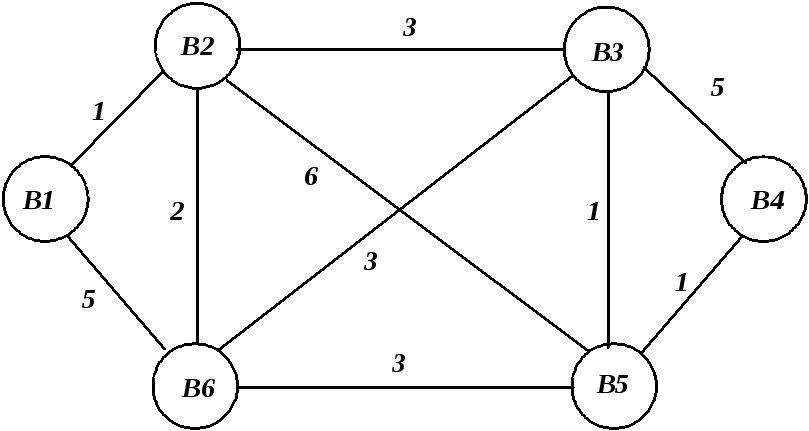
Рис.2

Початкова матриця

	1	2	3	4	5	6
1	0	1	∞	∞	∞	5
2	1	0	3	∞	6	2
3	∞	3	0	5	1	3
4	∞	∞	5	0	1	∞
5	∞	6	1	1	0	3
6	5	2	3	∞	3	0

На першій ітерації при матриця не змінюється. Тому розглянемо випадок . Матриця, отримана після другої ітерації:

	1	2	3	4	5	6
1	0	1	4	∞	7	3
2	1	0	3	∞	6	2
3	4	3	0	5	1	3
4	∞	∞	5	0	1	∞
5	7	6	1	1	0	3
6	3	2	3	∞	3	0

При цьому:

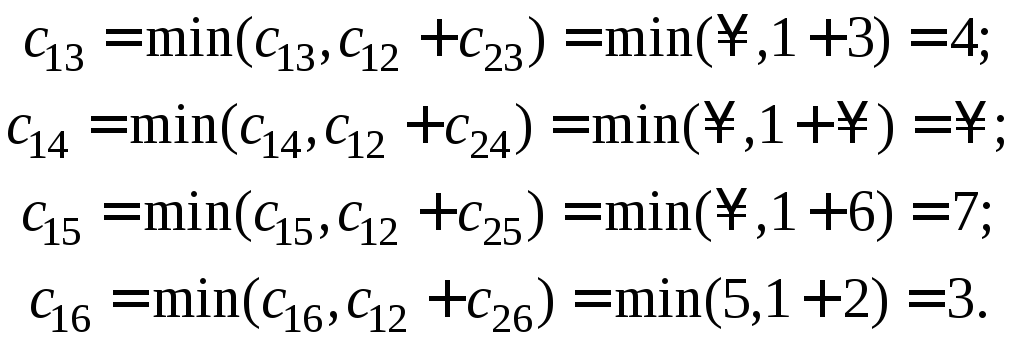
Отримані числа записані в першому рядку цієї матриці, аналогічно знайдені її інші рядки.

Кінцевий результат:

	1	2	3	4	5	6
1	0	1	4	6	5	3
2	1	0	3	5	4	2
3	4	3	0	2	1	3
4	6	5	2	0	1	4
5	5	4	1	1	0	3
6	3	2	3	4	3	0

Як правило, кількість ітерацій відповідає кількості вершин графа мережі поштового зв’язку.