Допоміжна таблиця для обчислення коефіцієнта кореляції Пірсона

і	х	у	ху	х2	у2
1	2	26,4	52,8	4	696,96
2	3,5	26,9	94,15	12,25	723,61
3	4	27,3	109,2	16	745,29
4	5,2	27,7	144,04	27,04	767,29
5	6,3	28,1	177,03	39,69	789,61
6	7,1	28,4	201,64	50,41	806,56
7	8,4	29,1	244,44	70,56	846,81
8	9,5	29,4	279,3	90,25	864,36
Разом	46	223,3	1 302,6	310,2	6 240,49

Тоді:

= 310,2 / 8 – (46 / 8) ²= 5,7125;

= 6 240,49 / 8 – (223,3 / 8) ²= 0,9536.

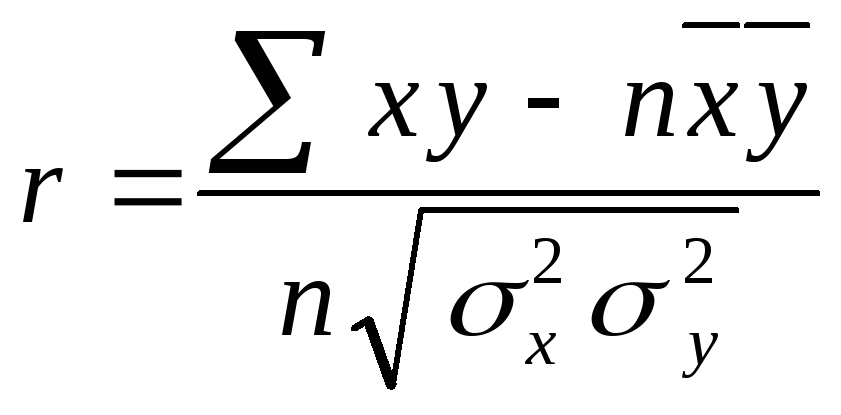== 0,997.

Для n = 8, r_кр = 0,71. Оскільки розраховане значення коефіцієнта кореляції Пірсона більше за його критичне значення, то зв’язок є істотним.

Коефіцієнт кореляції Пірсона набуває значень у межах , тому ха-рактеризує не лише щільність, а й напрямок зв’язку. Додатне значення свідчить про прямий зв’язок, а від’ємне – про обернений.

Відповідь: лінія регресії має вигляд: у = 25,57 + 0,408· х; лінійний коефіцієнт кореляції Пірсона r = 0,997 свідчить про щільний прямий зв’язок.

Приклад 2

Дані про споживання м’яса та м’ясопродуктів у домогосподарствах з різним рівнем середньодушового сукупного доходу наведено у таблиці:

Рівень середньодушового сукупного доходу	Кількість сімей	Споживання м’яса в середньому на члена сімї за рік, кг
Низький	6	48, 62, 40, 52, 50, 36
Середній	10	91 96 84 95 98 94 92 89 98 92
Високий	4	100 112 108 110

Встановити взаємозв’язок та оцінити його істотність і щільність за допомогою методу аналітичного групування.

Розв’язання:

Розрахуємо середні величини в кожній групі за формулою середньої арифметичної простої:

= (48 + 62 + 40 + 52 + 50 + 36) / 6 = 48;

= (91 + 96 + 84 + 95 + 98 + 94 + 92 + 89 + 98 + 92) / 10 = 84,6;

= (100 + 112 + 108 + 110) / 4 = 107,5.

Загальну середню для всієї сукупності обчислимо за формулою середньої арифметичної зваженої, де в якості окремих ознак беруться середні кожної групи, а частотами є обсяги відповідних груп:

= (48 × 6 + 84,6 × 10 + 107,5 × 4) / 20 = 78,2.

Визначаємо групові дисперсії за формулою:

.

Тоді: =(48 – 48)² + (62 – 48)² + (40 – 48)² + (52 – 48)² + (50 – 48)² +

+ (36 – 48)²  / 6 ≈ 70,67;

= (91 – 84,6)² + (96 – 84,6)² + (84 – 84,6)² + (95 – 84,6)² + (98 – 84,6)² +

+ (94 – 84,6)² + (92 – 84,6)² + (89 – 84,6)² + (98 – 84,6)² + (92 – 84,6)²  / 10 = 85,58;

= (100 – 107,5)² + (112 – 107,5)² + (108 – 107,5)² + (110 – 107,5)² / 4 =

= 20,75.

Середню з групових дисперсій розрахуємо за формулою:

= (70,67 × 6 + 85,58 × 10 + 20,75 × 4) / 20 = 68,14.

Міжгрупову дисперсію обчислимо за формулою:

(48 – 78,2)² × 6 + (84,6 – 78,2)² ×10 + (107,5 – 78,2)² × 4 / 20 = 465,79.

Використовуючи правило складання дисперсій , визначимо загальну дисперсію:

= 465,79 + 68,14 = 533,93.

Обчислимо кореляційне відношення:

= 465,79 / 533,93 = 0,872.

Критичне значення кореляційного відношення для обсягу сукупності 20 одиниць та трьох груп дорівнює 0,318.

Відповідь: Оскільки розраховане кореляційне відношення більше за його критичне значення, між рівнем середньодушового доходу та споживанням м’яса існує прямий щільний зв’язок.