Решите самостоятельно задачи:

1. Привести к простейшему виду уравнение

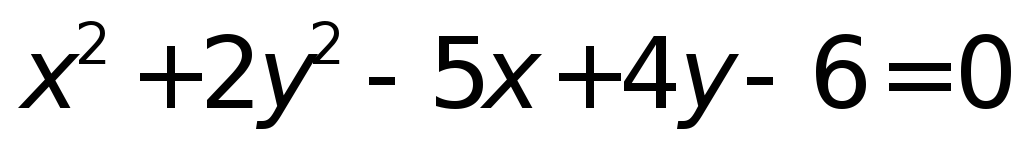
2. Уравнение асимптот гиперболы 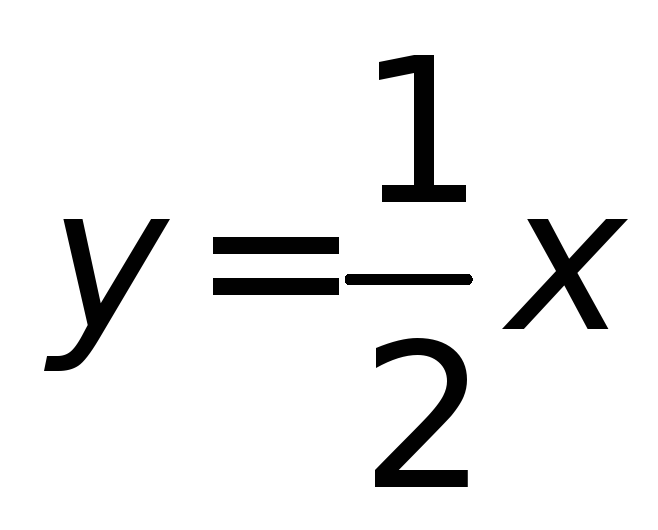и, а расстояние между фокусами. Найти уравнение гиперболы.

Задание №4

Для решения задачи № 4 следует иметь понятие о базисе.

Система изn линейно независимых векторов в n-мерном пространственазывается базисом.Векторы называются линейно независимыми, если равенство

(линейная комбинация этих векторов равна 0) выполняется только при нулевых значениях коэффициентов– всехприi=1,2…n.

Если это равенство имеет место при условии, что хотя бы один из коэффициентов отличен от нуля, тосистема векторов называется линейно зависимой.

В n-мерном пространстве линейно независимая система векторов не может содержать болееnвекторов.

Пусть задана система из nлинейных уравнений с nнеизвестными

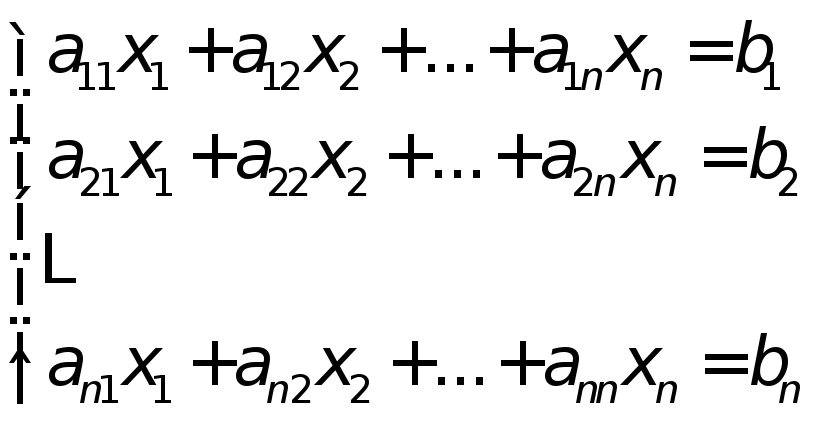
Матрица системы – набор из чисел-коэффициентов системы, так как число строк матрицы равно числу столбцов матрица называется квадратной.

Её определитель (для случая, когда n=3):

- определитель разложен по первой строке. Как определяются определители высших порядков, можно узнать в указанных ниже учебниках или в следующем разделе.

Итак, если определитель системы , то система имеет единственное решение , которое можно найти поформулам Крамера

Где определитель матрицы системы, а определитель матрицы, полученной из матрицы системыАзаменойi-го столбца на столбец свободных членов .

Пример 1. Решим задачу разложения вектора по базису:

Пусть даны вектора

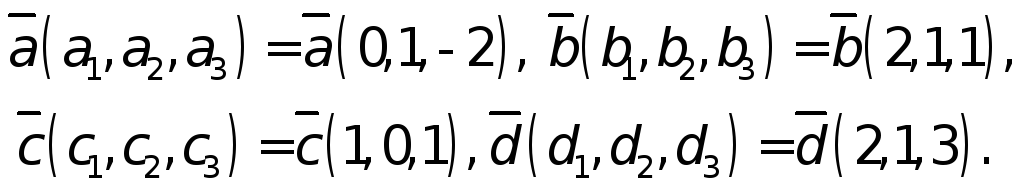
Решение: Покажем в начале, что векторыиобразуют базис. Система векторов образует базис, если эти векторы линейно независимы, а соответствующее векторное уравнение

Обращается в тождество только при λ₁=λ₂=λ₃=0.

Используя координаты векторов , составим систему линейных уравнений, эквивалентную векторному уравнению

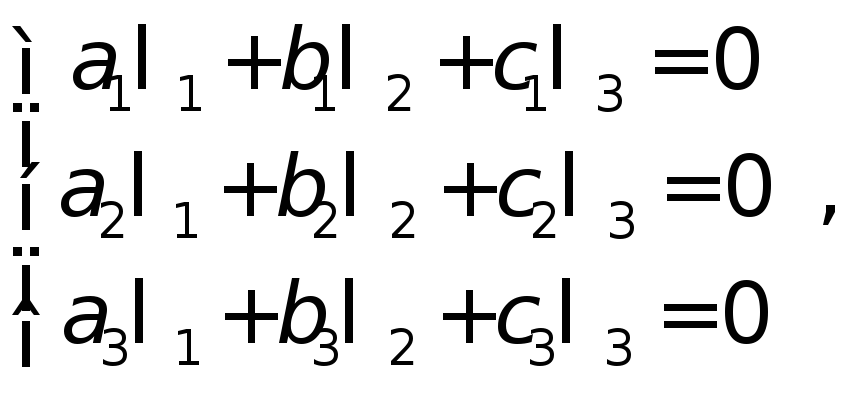
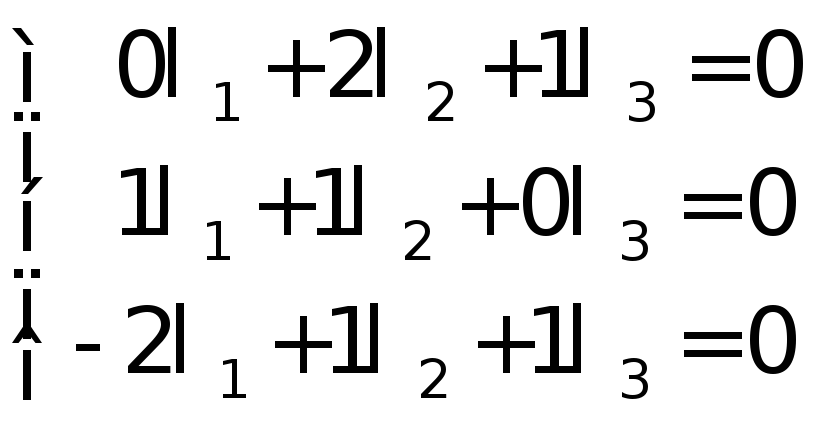
Вычисляем определитель Δ данной системы

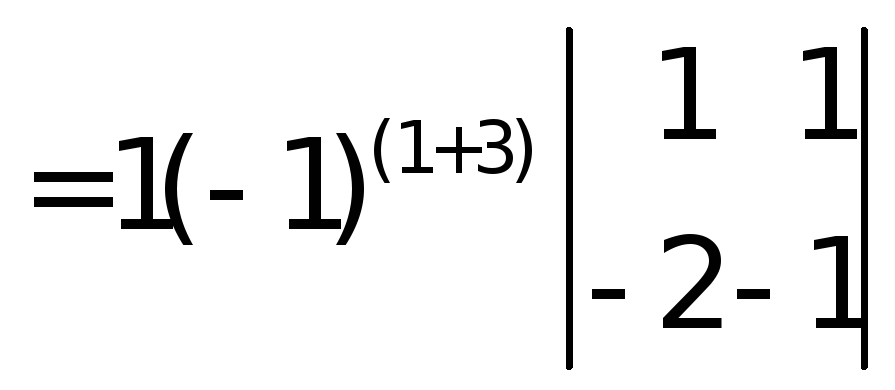=1(-1)-1(-2)=1.

Так как Δ 0, то система имеет только нулевое решение (λ₁,λ₂,λ₃)=(0,0,0).Это следует из того факта, что приb_i =0 все определители при неизвестных в формулах Крамера равны нулю Δ₁ = Δ₂=Δ₃= 0.

Следовательно, векторы образуют базис.

Найдем координаты вектора в базисе. Четыре вектора в трехмерном пространстве всегда линейно зависимы, т.е. векторесть линейная комбинация векторов

.

Аналогично предыдущему случаю составим систему уравнений для определения координат λ₁,λ₂,λ₃ векторав базисе

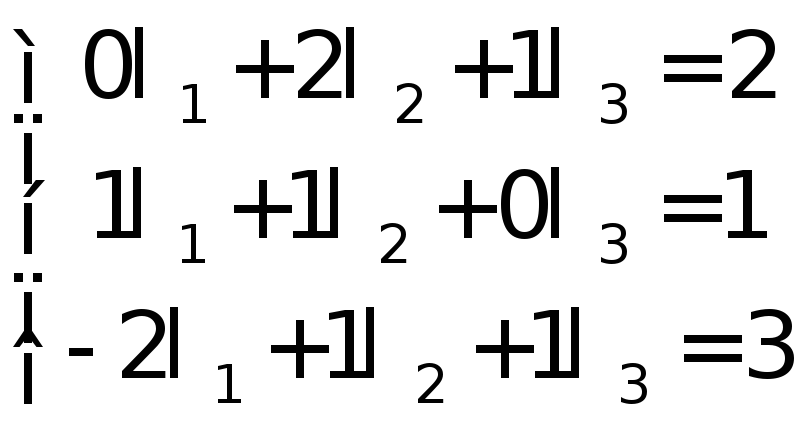
Определитель системы совпадает с определителем системы и не равен нулю Δ=1 0. Следовательно, система имеет единственное решение. По формулам находимλ₁,λ₂иλ₃

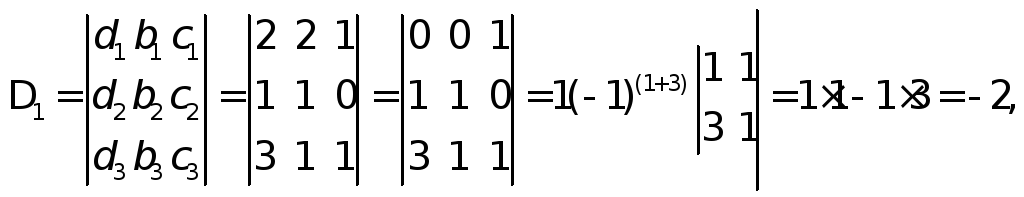
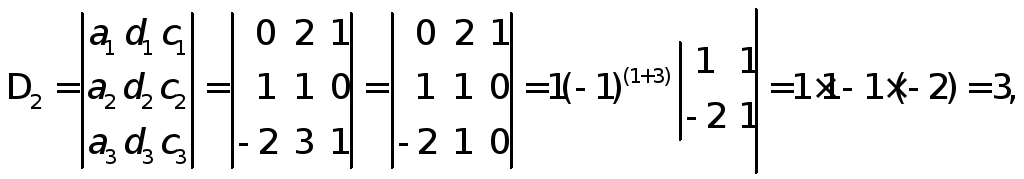
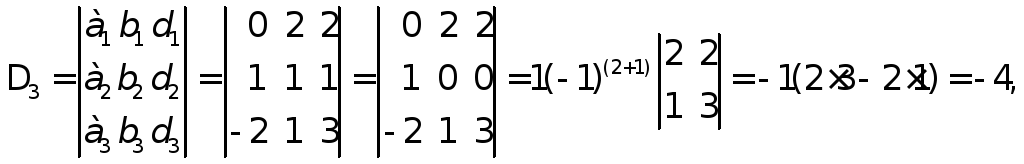
λ₁=Δ₁/Δ=-2/1=-2,λ₂=Δ₂/Δ=3/1=3,λ₃=Δ₃/Δ=-4/1=-4,

Итак, разложение вектора по базисуимеет вид:

Если векторы заданы в базисе, то в этом базисе векторимеет координаты(2;1;3).

Студенту рекомендуется самостоятельно нарисовать векторы в пространствеR³и сравнить полученные значенияλ_icо значениями, полученными графически.

Следующую задачу решите самостоятельно:

4.1. Решить систему уравнений методом Крамера .