Методические указания для студентов

Методические указания предназначено для студентов Iкурса инженерно- технических специальностей, включая и специальность ЭВМ. Для решения каждой задачи контрольных заданий приведены необходимые теоретические сведения и дано типовое решение в соответствующем разделе пособия.

В соответствии с требованиями дистанционного обучения в каждом разделе приведён список вопросов и задач на данную тему для самостоятельной работы.

В конце методических указаниях приведены ответы, краткие или подробные указания по решению задач. Для более тщательного и глубокого изучения теоретического материала и развития навыков по решению задач в пособии разработан предметный указатель и список рекомендуемой литературы. Методические указания соответствуют контрольным заданиям для студентов – заочников Iкурса инженерно – технических специальностей: Задания на контрольные работы №1-4 (шифры 3/1/1 , 3/2/1 и 3/2/5)

Задание №1.

Для решения контрольной работы №1 по математике и контрольной работы №1 по курсу алгебра и геометрия следует изучить разделы векторной алгебры, линейной алгебры и аналитической геометрии любых учебников. Для решения задач первой контрольной понадобятся следующие понятия и факты:

Для решения первой задачи:

Определители 2и3порядков

-определитель2-го порядка

Заметим, что у элемента определителя -номер строки, а-номер столбца

-

- определитель 3порядка

Векторы и действия над ними.

В декартовой прямоугольной системе координат вектор (или) имеющий начало в точкеА(3,4,0)и конец в точкеВ(5,7,5) имеет следующие координаты (5-3; 7-4;5-0)или (2,3,5)

Векторы можно складыватьи если=+, где(2,3,5)а(4,5,6)то (2+4;3+5;5+6) =(6,8,11)

Можно умножить вектор на число,например если(2,3,5) умножить на(-2)получим вектор -2(-4,-6,-10)

Длина (модуль) вектораобозначаетсяи считается по формуле

=

для (2,3,5)

||=

Итак, мы имеем заданную в пространстве декартову прямоугольную систему координат ,,- единичные векторы (орты) положительных направлений осейИ когда мы пишем, что (2,3,5)это означает, что=

Тройку векторов называют ортонормированным координатным базисом.

2,3,5 - координаты вектора, а

2, 3, 5-компоненты вектора.

Пусть имеем два вектора (2,3,5)и (6,8,11).

Скалярным произведением вектора на вектор называется число (,) =, гдеугол междуи.

В координатной форме

(,) =- т.е. сумме произведений одноимённых координат

=

Скалярное произведение можно использовать, чтобы найти длину вектора.

Скалярный квадрат

=

таким образом

==

С помощью скалярного произведения можно найти угол между двумя векторами

=, значит

=

Векторным произведением наназывается вектор, обозначаемыйилии такой, что:

1) длина |[a, b]| = |a|·|b|·sin–т.е. численно равно площади параллелограмма, построенного на векторахи

2) перпендикулярен плоскости векторови

3) вектора ,, исоставляют правую тройку, т.е. расположены как большой, указательный и средний палец правой руки.

Координатная форма векторного произведения

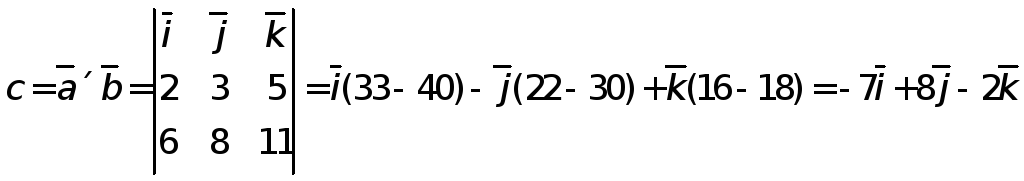
или (-7,8,-2)

Смешанное произведениетрех векторов,иобозначаетсяи равно, то есть векторной произведениенаскалярно умножено на(значит, это число – скаляр)

Численно модуль смешанного произведения равен объему параллелепипеда, построенного на векторах ,и.

Координатная форма смешанного произведения

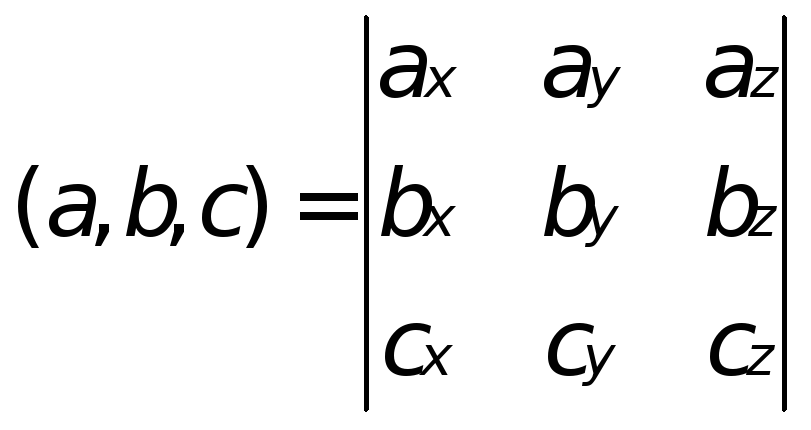
Поскольку в случае компланарности векторов объем соответствующего параллелепипеда равен нулю, то условием компланарности является равенство нулю их смешанного произведения

Плоскость и прямая в пространстве.

Рассмотрим произвольную плоскость и на ней вектор-нормаль , то есть вектор, перпендикулярный плоскости и фиксированную точку.Возьмем текущую точку,координаты которой меняются так, что точкаостается в плоскости, таким образом вектортакже всегда, при любых движениях точкилежит в плоскости.

Итак, вектор лежит в плоскости, а векторей перпендикулярен. Тогда их скалярное произведение равно нулю:

, или, где

Это общее уравнение плоскости.

Если , то разделив все члены уравнения наполучимуравнение плоскости в отрезках

.

абсцисса, ордината и аппликата точек пересечения плоскости с осями

Рассмотрим три заданные точки в пространстве ,и.

Как известно, три точки определяют плоскость. Введём текущую точку , координаты которой меняются, но она не выходит за рамки плоскости. Рассмотри три вектораВсе они лежат в плоскости, то есть они компланарны и их смешанное произведение равно нулю.

Это уравнение плоскости, проходящей через три заданные точки.

Рассмотрим в пространстве прямую. Её можно задать, задав фиксированную точку, через которую она проходит и, задав её направление при помощи вектора.

Итак, напишем уравнение прямой, проходящей через заданную точку и параллельной направляющему вектору. Опять возьмем текущую точку на прямой, т.е. точку, координаты которой меняются так, чтобы она не вышла за пределы этой прямой. Векторлежит на прямой и, значит, коллинеарен вектору.

Если вектора коллинеарны, то их координаты пропорциональны.

- это и естьканонические уравнения прямой в пространстве.

Обозначим отношение

за

Это параметрические уравнения прямой.

Более подробно этот материал можно найти в , главы 1 и 2; в§1,2,5,6,9,10,12,13; вглавы 1,2,3 можно найти похожие задачи.

Пример 1. Задана пирамида с вершинами ,,,.

Зная координаты начала и конца вектора , мы можем найти его координаты:

или

Аналогично найдем

1. Теперь найдем уголмежду реброми гранью .

Вообще говоря, найти угол между прямой и плоскостью, а угол как раз и является углом между прямойи плоскостью,- это угол между прямой и её проекцией на плоскость – задача непростая. Уголнайти проще, а ведь в сумме они составляют.

Значит, найдя , найдем и=-.

Итак, ищем : это угол между вектором-нормальюк плоскостии вектором.

Отыщем сначала . Какой вектор мы можем выбрать в качестве перпендикуляра к плоскости? Векторное произведение любых двух векторов, лежащих в плоскости, перпендикулярно плоскости. Возьмем векторное произведение.

==

=

Нас интересует уголмежду=и.

Скалярное произведение

следовательно

Если , то

- угол между ребром пирамиды и гранью.

2. Найдем площадь грани.

Площадь грани – это площадь треугольника и половина площади параллелограмма, построенного на векторахи.

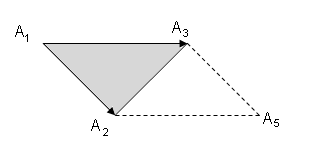
Но мы знаем из определения векторного произведения, что длина вектора =численно равна площади этого параллелограмма. Длину векторамы считали в пункте 1 и она равна.

Итак, площадь грани =

3. Найдем объем пирамиды;

Объем пирамиды равен =

Если отбросить коэффициент , то получим=- объем призмы, в основании которой лежит, т.е. объем пирамиды равенобъема призмы.

А объем параллелепипеда, основанием которого является параллелограмм в 2 раза больше объема призмы, следовательно, объём пирамиды - этообъема параллелепипеда.

Но объем данного параллелепипеда численно равен модулю смешанного произведения векторов, на которых построен параллелепипед

4. Найдем уравнения прямой- это уравнения прямой, проходящей через заданную точкув направлении, заданном вектором. Итак, пишем уравнение прямой, проходящей через точкуА₁ (1,2,3)в направлении вектора

5. Уравнение плоскости:

У нас имеется три точки, лежащие в интересующей нас плоскости, значит, используем уравнение плоскости, проходящей через 3 точки:

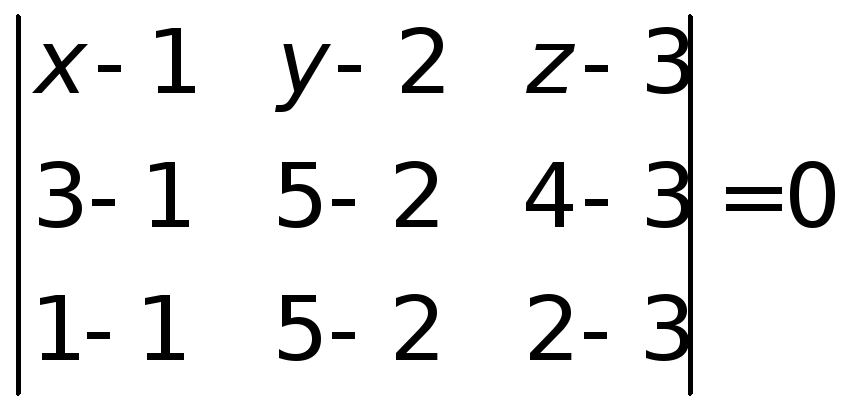
или

Раскладываем определитель по первой строке

6. Находим уравнения высоты, опущенной из вершинына грань.

Раз эта прямая-высота – она перпендикулярна плоскости , значит, в качестве направляющего вектора прямой можно взять вектор, перпендикулярный.

Высота опущена из вершины - значит искомая прямая проходит через точку.

Итак, пишем уравнения прямой, проходящей через заданную точку(3,4,8)в направлении заданного вектора (-6,2,6).

или

Наконец, найдем координаты точки пересечения высоты с нижней гранью.

То есть точку пересечения прямой и плоскости

Перейдем к параметрическому виду уравнений прямой:

и подставим ив уравнение плоскости:

Итак, высота пирамиды пересекается с нижней гранью в точке .