Примеры построения математических моделей задач о перевозках Задача № 1
Производится загрузка товара (в контейнерах) на сухогруз. Какой минимальной грузоподъемности следует использовать сухогруз, чтобы погрузить на него товар ценностью не менее 750 тыс.$ и объемом груза не более 280 м. куб, при условии, что таможенный сбор не превысит 20% стоимости груза, а стоимость погрузки не превысит 0.5% от стоимости груза. Исходные данные приведены в таблице 11.
Решение
Введем обозначения:
-
стоимость контейнера груза i
–го типа,
,
(тыс.$);
-
стоимость погрузки контейнера i
–го типа,
,
($);
-
объем контейнера груза i
–го типа,
,
(м. куб.);
-
вес
контейнера
груза i
–го типа,
,
(т);
-
таможенный сбор за контейнер груза i
–го типа,
,
(%);
-
возможности порта по запасам контейнеров
груза i
–го типа,
,
(шт.);
Неизвестные:
-
количество контейнеров i
– го
типа, помещаемых на сухогруз,
;
Ограничения:
а) по возможностям порта
б) по стоимости погруженных контейнеров
в) по объему погруженных контейнеров
г) по таможенным платежам
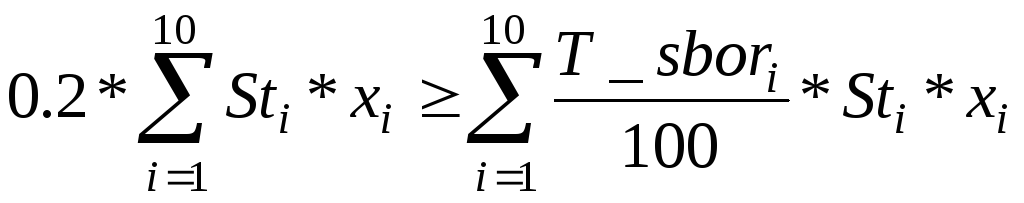
д) по стоимости погрузки
Функция цели:
Задача № 2
Диспетчер такси на основании информации о местоположении освободившихся машин и по адресам поступивших вызовов должен принять решение о направлении машин на новые заявки так, чтобы минимизировать холостой пробег машин. Расстояние (в км) между районами (всего 10 районов) приведено в таблице15. Свободные машины в районах: 1, 1, 2, 3, 3, 10, 10, 10, 10. Заявки в районах 3, 6, 8, 8, 10.
Решение
Введем обозначения:
-
расстояние между i
– ым и j-тым
районами города,
,
;
-
возможности i
– ого района по количеству свободных
такси,
,
(
,
,
,
,
остальные =0);
-
потребности i
– ого района в свободных такси,
,
(
);
Неизвестные:
-
количество такси, направляемых из i
– го
района города для обслуживания заявки
в j-тый
район города,
,
;
Ограничения:
а) по неизвестным
,
целочисленные;
б) по возможностям районов
в) по потребностям районов
Функция цели:
ПримерЫ решения задач о ПЕРЕВОЗКах в What’s Best
Задача № 1
10 торговых точек получают товар с 3-х складов, в которых хранится однотипный товар. Известны расстояния (км) между всеми складами и торговыми точками. Исходные данные приведены в таблице 23. Закрепить торговые точки за складами так, чтобы минимизировать общее расстояние перевозок, при этом, чтобы за каждым складом были закреплены не менее 2-х и не более 5-и торговых точек. Каждая торговая точка должна быть закреплена только за одним складом.
Таблица 23
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Возможности складов |
|
Склад1 |
5 |
1,2 |
2,5 |
5 |
1 |
2 |
2,5 |
5 |
4 |
6 |
30 |
|
Склад2 |
4 |
3,2 |
1 |
2,5 |
1,2 |
1 |
2 |
3,8 |
4 |
3 |
35 |
|
Склад3 |
3 |
4 |
2 |
1 |
1,8 |
2,1 |
1 |
2,5 |
3,3 |
4,2 |
25 |
|
Потребности магазинов |
2 |
4 |
8 |
6 |
1,5 |
7 |
1 |
4,7 |
5 |
3 |
|
Решение
Введем обозначения:
-
расстояние между i
– ым магазином и j-тым
складом,
,
;
-
возможности j
– ого склада по наличию товара,
;
-
потребности i
– ого магазина,
;
Неизвестные:
-
закрепление i
– го
магазина за j-тым
складом,
,
;
Ограничения:
а) по неизвестным
,
целочисленные;
б) по возможностям складов
в) по количеству закрепленных торговых точек
г) по закреплению каждого магазина только за одним складом
Функция цели:
