2.2. Предел функции

Пусть функция определена в некоторой окрестности, за исключением, быть может, самой точки.

Определение 5. Число А называется пределом функции в точке, если, чтои при этом пишут. у

Геометрически это представля-

ется следующим образом: ,

что .А

Упрощенно это определение

можно представить так:

Число А называется пределом х

функции прих, стремящимся а

к числу а, если точка приближается к числуА, когда точка х приближается к а.

Пример 3. Покажем, что для функции .

Зададим произвольное и определим. Запишем неравенство

.

Существенным понятием, особенно при нахождении пределов функции, являются односторонние пределы.

Определение 6. Число А называется правым (левым) пределом функ-

ции в точке, если, чтои при этом пишут

.

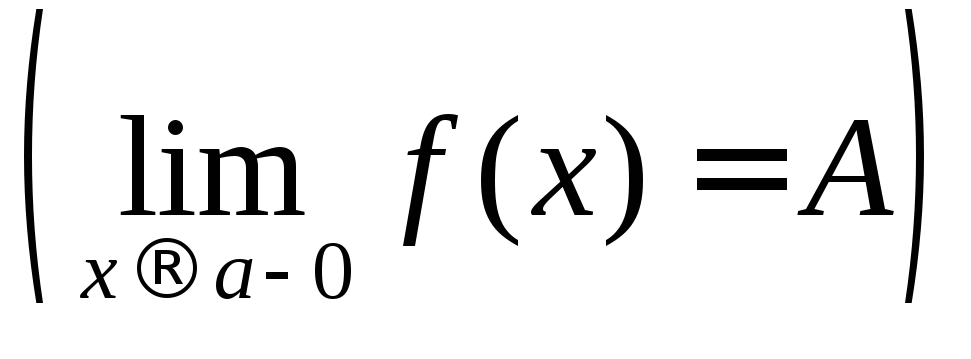Связь между односторонними пределами и пределом функции уста-навливает следующая теорема.

Теорема. Если функция в точкеимеет предел, то. Верно и обратное.

Из таких же соображений определяется и предел функции при .

Определение 7. Число А называется пределом функции при, если, чтовыполняется неравенствои при этом пишуту

, если и

, если .А

Геометрически это выглядит

следующим образом: О М х

что будет.

Пример 4. Покажем, что для функции .

Зададим и определимМ. Запишем неравенство

.

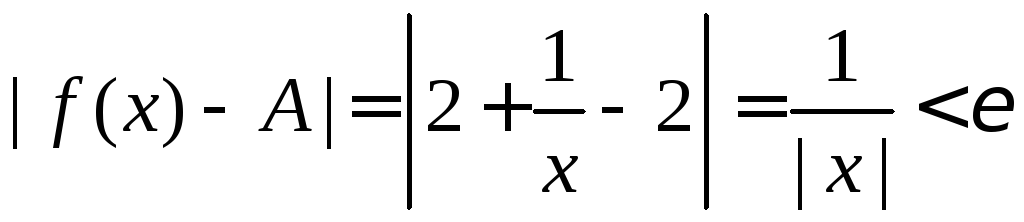
Замечание 2. Иногда удобно использовать другое, эквивалентное опре-деление предела функции:

Число А называется пределом функции в точке, если.

Лекция № 15

2.3. Бесконечно малые и бесконечно большие величины

Определение 1. Функция называется бесконечно малой величиной (б.м.в.) при , если.

Напомним это определение: , что

.

Определение 2. Функция называется бесконечно большой величиной (б.б.в.) при , если, чтои при этом пишут.

Пример 1. Покажем, что для функции

Зададим . Получим неравенство

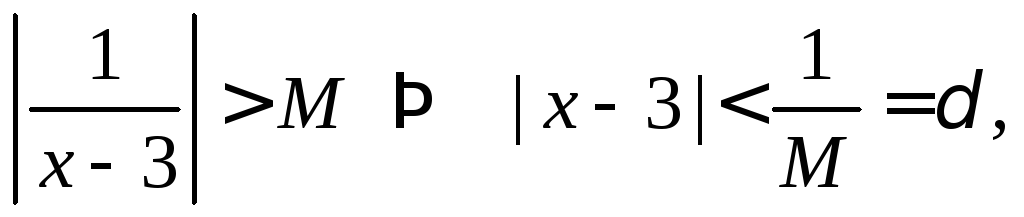
т.е. в этой окрестности точки значения функции по модулю будут больше заданного числаМ.

Замечание 1. При определении б.м.в. и б.б.в. следует обратить внимание на фразу “при “, так, например, функцияявляется б.м.в. прии б.б.в. при, что видно, в частности, из графика этой функции.

Замечание 2. Все б.б.в. являются неограниченными функциями. Обрат-ное, вообще говоря, неверно, что видно из примера.

Пример 2. Очевидно, функция является неограниченной при, но она не является б.б.в. Например, для последовательности,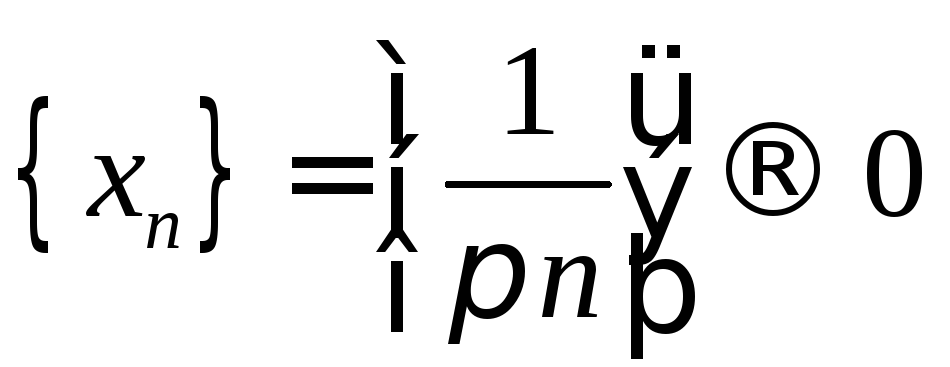

Замечание 3. Б.м.в. принято обозначать:

Б.м.в. и б.б.в. обладают следующими свойствами:

1. Сумма конечного числа б.м.в. есть б.м.в..

Не нарушая общности, рассмотрим случай двух б.м.в. Зададим для суммы . Тогда в силу определения б.м.в. одновременно выполняется

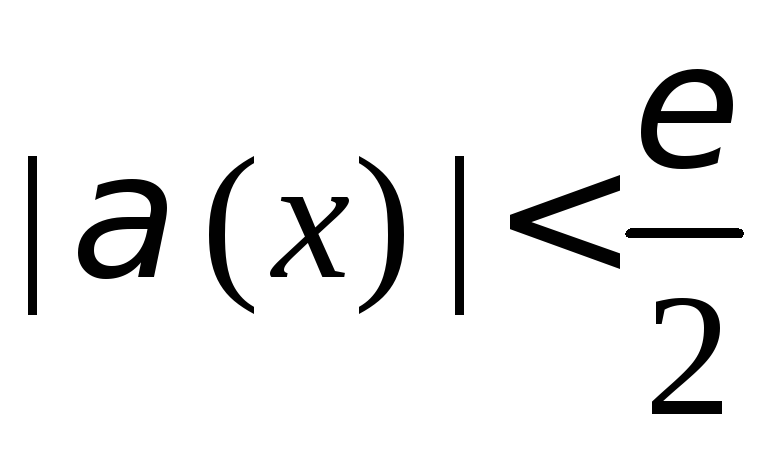и , т.е. сумма б.м.в.

2. Произведение ограниченной функции на б.м.в. есть б.м.в.

Доказывается аналогично с учетом, что 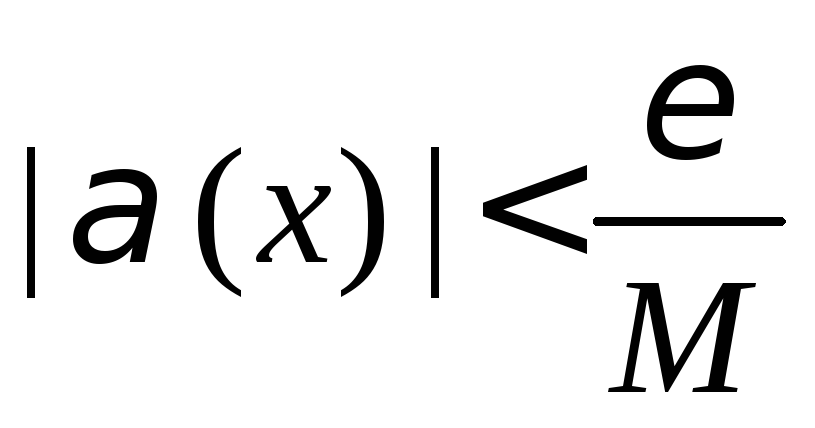, где.

3. Если  б.м.в. при , то б.б.в. при . Верно и обратное.

Пусть  б.м.в. Это означает, что . Тогда, т.е. б.б.в. Аналогично доказывается и обратное утверждение.