3.2. Основные теоремы о непрерывных функциях.

Непрерывность элементарных функций

Используя теоремы 13 о пределах функции (п.2.5), можно доказать следующие теоремы:

Теорема 1. Сумма конечного числа непрерывных функций является непрерывной функцией.

Пусть функции непрерывны в точкех₀ и

.

Тогда имеем

ч.т.д.

Теорема 2. Произведение конечного числа непрерывных функций является непрерывной функцией.

Доказательство аналогично.

Теорема 3. Частное двух непрерывных функций является непрерывной функцией, если знаменатель в рассматриваемой точке не равен нулю.

Доказательство аналогично.

Теорема 4. Пусть функция непрерывна в точкеи₀, а функция непрерывна в точкех₀ и пусть . Тогда сложная функция непрерывна в точкех₀.

Здесь была использована подстановка и условие непрерыв-ности функциив точкех₀.

В результате доказательств этих теорем и непрерывности основных элементарных функций приходим к важной обобщающей теореме:

Теорема 5. Все элементарные функции непрерывны в своей области определения.

3.3. Классификация точек разрыва функции

Определение 4. Если в точке х₀ нарушается условие непрерывности функции , то функция называется разрывной в точкех₀, а точка х₀  точкой разрыва функции.

Определение 5. Точка х₀ называется точкой разрыва первого рода, если существуют конечные односторонние пределы функции, не равные между собой, т.е. .

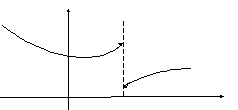
Схематичный вид функции в точке разрыва первого рода:

у

0 х₀ х

Пример 2. Функции, имеющие разрывы первого рода:

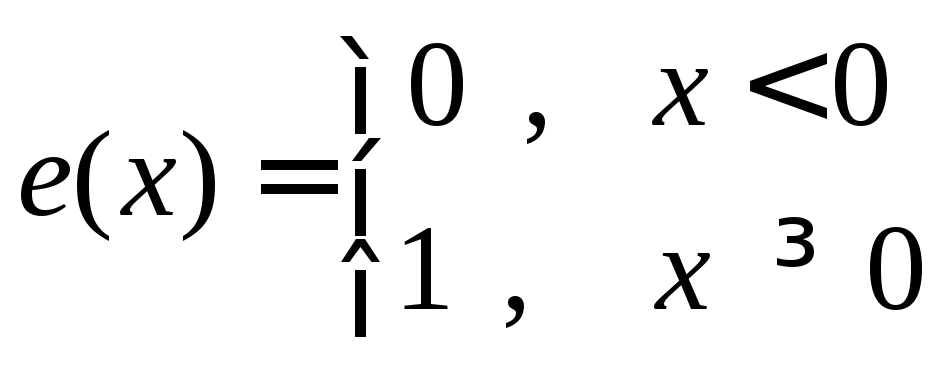;  целая часть числа х.

Определение 6. Точка х₀ называется точкой устранимого разрыва, если .

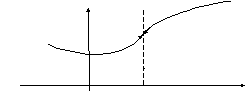
В этом случае полагают и точках₀ стано-вится точкой непрерывности. Функция в этой точке имеет вид

у

0 х₀ х

Пример 3. Для функции точках₀ = 0 является точкой устранимого разрыва.

Определение 7. Точка х₀ называется точкой разрыва второго рода, если хотя бы один из односторонних пределов не существует или равен бесконечности.

Пример 4. Покажем, что функция в точкех₀ = 1 имеет разрыв второго рода.

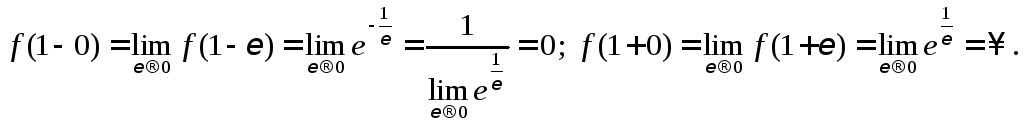
Пример 5. Покажем, что функция 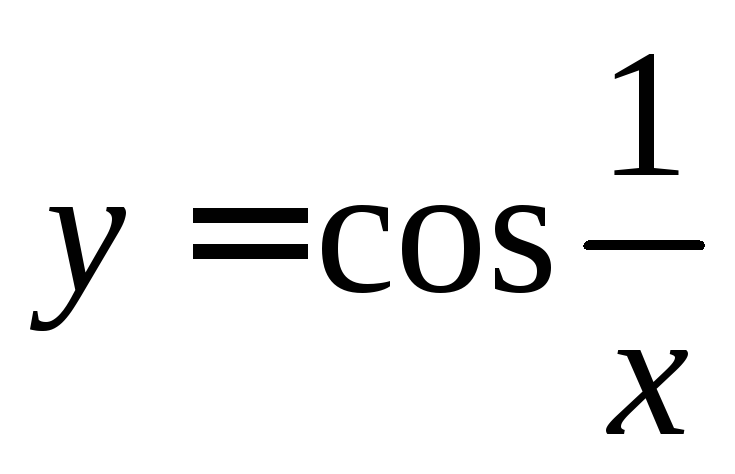в точкех₀ = 0 имеет разрыв второго рода.

Рассмотрим последовательность :

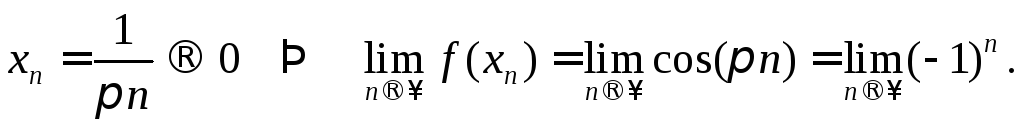
Как показано в п.2.2 последний предел не существует, т.е. имеем разрыв второго рода.

3.4. Свойства функций, непрерывных на отрезке

Теоремы,описывающие эти свойства, проиллюстрируем на графиках.

Теорема 1. Если непрерывна на, то она ограничена на, т.е..

Т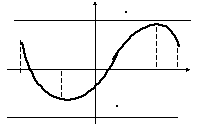еорема 2. Если непрерывна на, то насуществуют её наибольшее и наименьшееу

значения, т.е. М

и пишут

c

а 0 d b x

M

Теорема 3. Если непрерывна наи принимает на концах отрезка неравные значения, то дляy

любого промежуточного значения М

между этими числами существует по М

крайней мере одна точка ,

для которой .

0 a c b x

Следствие. Если непрерывная на функцияпринимает на концах значения разных знаков, тоy

существует по крайней мере одна

точка , в которой.a c b x

Этот факт используется для 0

нахождения корней уравнения.