
- •Дифференциальные уравнения Лекция № 37. Тема 1 : Введение
- •1.1. Задачи, приводящие к дифференциальным уравнениям
- •1.2. Определение дифференциального уравнения
- •Тема 2: Дифференциальные уравнения первого порядка
- •2.1. Общие понятия. Теорема существования и единственности
- •2.2. Уравнения с разделяющимися переменными
- •Лекция № 38
- •2.3. Однородные уравнения
- •Лекция № 39. Тема 3 : ду высших порядков
- •3.1. Определение ду п-го порядка
- •3.2. Уравнения, допускающие понижение порядка
- •4.2. Теорема о структуре общего решения лоду-2
- •Лекция № 40
- •4.3. Лоду-2 с постоянными коэффициентами
- •4.4. Линейные неоднородные дифференциальные уравнения второго порядка
- •4.5. Метод вариации произвольных постоянных (метод Лагранжа)
4.2. Теорема о структуре общего решения лоду-2
Теорема 4.
Если функции
![]() и
и![]()
два ЛНЗ решения уравне-ния (3), то его
общее решение имеет вид
два ЛНЗ решения уравне-ния (3), то его
общее решение имеет вид
![]() ,
где
,
где![]() и
и![]() произвольные константы.
произвольные константы.
Вначале покажем,
что
![]() является решением уравнения (3), для
чего подставим его в (3) и сгруппируем
члены при
является решением уравнения (3), для
чего подставим его в (3) и сгруппируем
члены при![]() и
и![]() :
:
![]() .
.
Далее покажем, что
для любых начальных условий вида
![]()
![]() можно найти значения
можно найти значения![]() и
и![]() ,
при которых такое решение удовлетворяло
бы им.
,
при которых такое решение удовлетворяло
бы им.
Подставим в эти
условия
![]() ,
тогда получим систему для определения
значений
,
тогда получим систему для определения
значений![]() и
и![]()
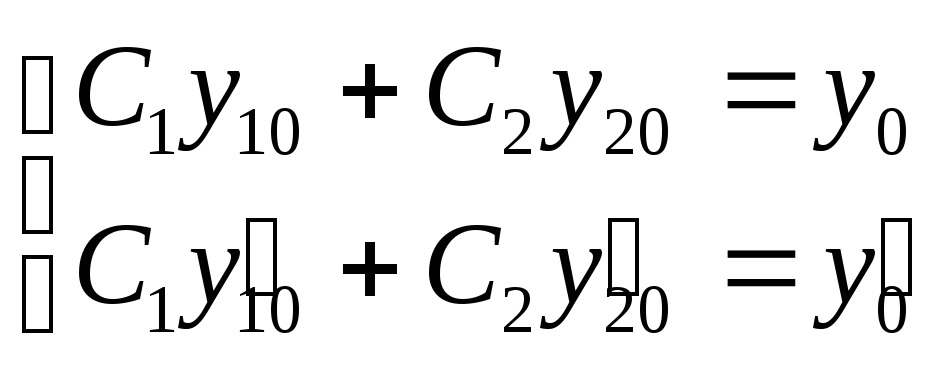 .
(5)
.
(5)
с определителем Вронского
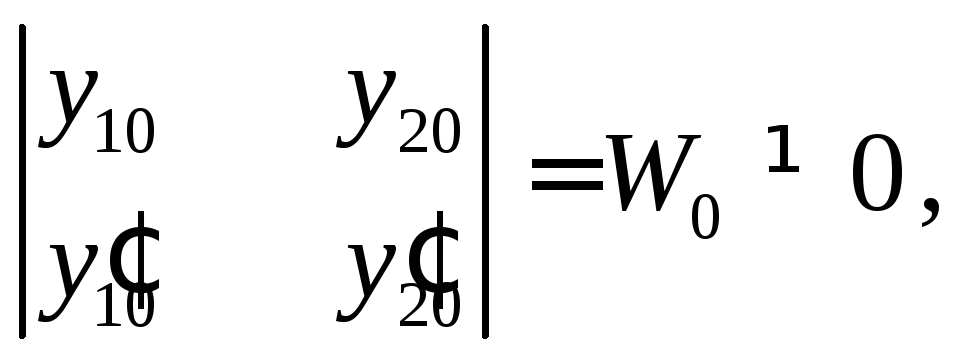
так как
![]() и
и![]() - ЛНЗ решения уравнения (3).
- ЛНЗ решения уравнения (3).
Из решения системы
(5) определяем
![]() и
и![]() .
Таким образом,
.
Таким образом,
![]()
является общим решением уравнения (3).
Лекция № 40
4.3. Лоду-2 с постоянными коэффициентами
Общий вид ЛОДУ-2
![]() ,
(1)
,
(1)
где
![]()
Будем искать
решение этого уравнения в виде
![]() .
.
Подставим в уравнение (1):
![]() (2)
(2)
Уравнение (2) называется характеристическим уравнением.
В зависимости от значений корней характеристического уравнения возможны следующие три случая:
1.
Корни уравнения
![]() и
и![]() действительные и
действительные и![]() .
.
Тогда, очевидно,
что
![]() и
и![]() .
Эти решения ЛНЗ, так как
.
Эти решения ЛНЗ, так как
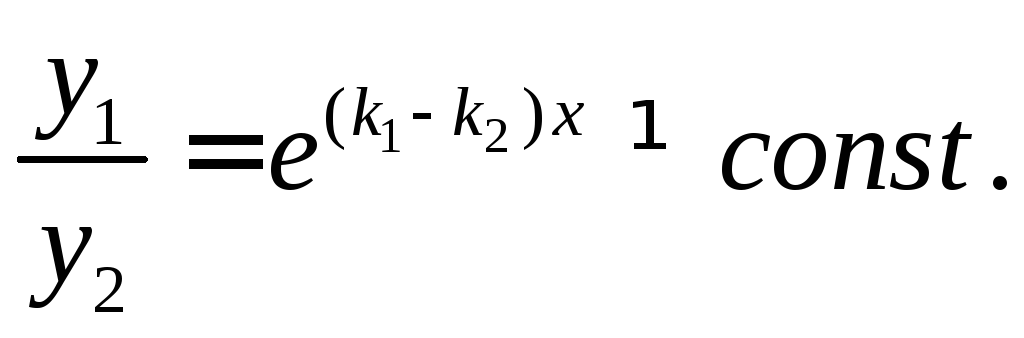
В этом случае общее решение примет вид
![]() .
(3)
.
(3)
Пример 1.
Найти общее решение уравнения
![]()
Составим характеристическое уравнение:
![]()
Воспользуемся формулой (3):
![]() .
.
2.
Корни
![]() и
и![]() действительные и
действительные и![]()
Тогда в качестве
первого частного решения можно взять
![]() .
Покажем, что в этом случае, является
решением также функция
.
Покажем, что в этом случае, является
решением также функция![]() .
Подставим её в уравнение и с учетом
теоремы Виета, получим
.
Подставим её в уравнение и с учетом
теоремы Виета, получим
![]() .
.
Эти решения ЛНЗ,
так как
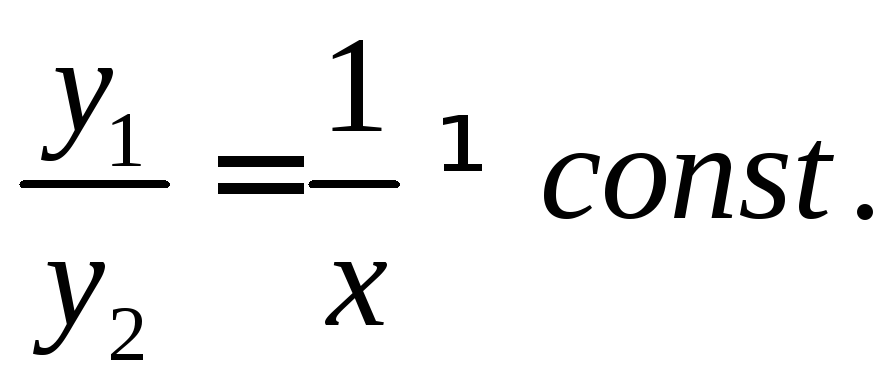
В этом случае общее решение примет вид
![]() .
(4)
.
(4)
Пример 2.
Найти общее решение уравнения
![]()
Составим характеристическое уравнени
![]()
Воспользуемся формулой (4)
![]() .
.
3.
Корни комплексно-сопряженные, т.е.
![]() .
.
Вначале покажем,
что если
![]() является решением уравнения (1), то этому
уравнению удовлетворяют функцииu
и v.
Подставим
является решением уравнения (1), то этому
уравнению удовлетворяют функцииu
и v.
Подставим
![]() в уравнение (1) и выделим действительную
и мнимую части:
в уравнение (1) и выделим действительную
и мнимую части:
![]()
Подчеркнутый член и выражение в скобках равны нулю.
Итак, в этом случае частные решения имеют вид
![]() и
и
![]() .
.
Если воспользоваться формулой Эйлера, которая будет доказана позже,
![]() ,
,
то
![]()
![]()
и, как показано выше, решениями уравнения (1) будут являться функции:
![]()
Очевидно, линейно-независимыми среди них будут
![]() ,
,
Так как
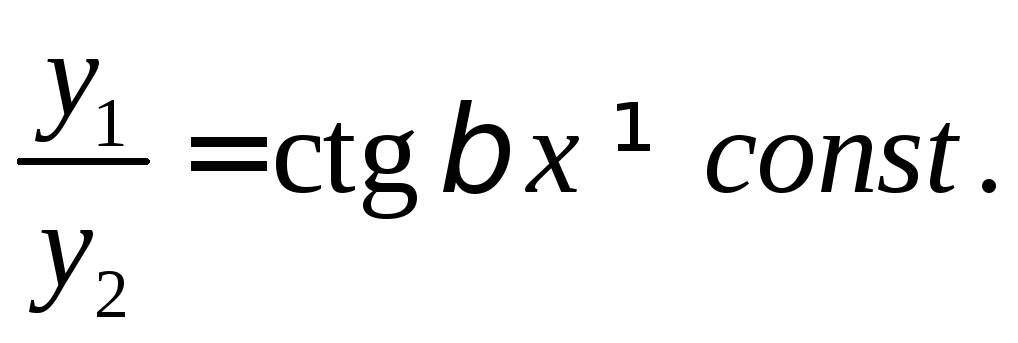
Окончательно, общее решение будет иметь вид
![]() .
(5)
.
(5)
Пример 3.
Найти общее решение уравнения
![]() .
.
Составим характеристическое уравнение:
![]()
Воспользуемся формулой (5):
![]() .
.
4.4. Линейные неоднородные дифференциальные уравнения второго порядка
Общий вид линейного неоднородного дифференциального уравнения второго порядка (ЛНДУ-2)
![]() (6)
(6)
гдефункции
![]() непрерывнынанекотором отрезке
непрерывнынанекотором отрезке
![]() .
.
Ему соответствует однородное уравнение
![]() (7)
(7)
Пусть известно общее решение уравнения (7)
![]() .
(8)
.
(8)
Теорема (о
структуре общего решения ЛНДУ-2). Общее
решение ЛНДУ-2 является суммой частного
решения
![]() уравнения (6) и общего решения
уравнения (6) и общего решения![]() соответствующего однородного (7).
соответствующего однородного (7).
Вначале покажем,
что
![]() является решением уравнения (6), для чего
подставим его в уравнение (6) и
сгруппируем члены
является решением уравнения (6), для чего
подставим его в уравнение (6) и
сгруппируем члены
![]() .
.
Сумма первых трёх
членов левой части равенства равна
нулю, так как
![]()
общее решение однородного уравнения,
а сумма остальных трёх членов равна
общее решение однородного уравнения,
а сумма остальных трёх членов равна
![]() ,
так как
,
так как![]()
есть частное решение уравнения (6).
есть частное решение уравнения (6).
Таким образом,
![]() является решением уравнения (6).
является решением уравнения (6).
Теперь покажем,
что для любых начальных условий вида
![]() можно найти значения
можно найти значения![]() и
и![]() ,
при которых решение удовлетворяло бы
им. Подставим решение
,
при которых решение удовлетворяло бы
им. Подставим решение
![]()
в эти условия, тогда получим систему
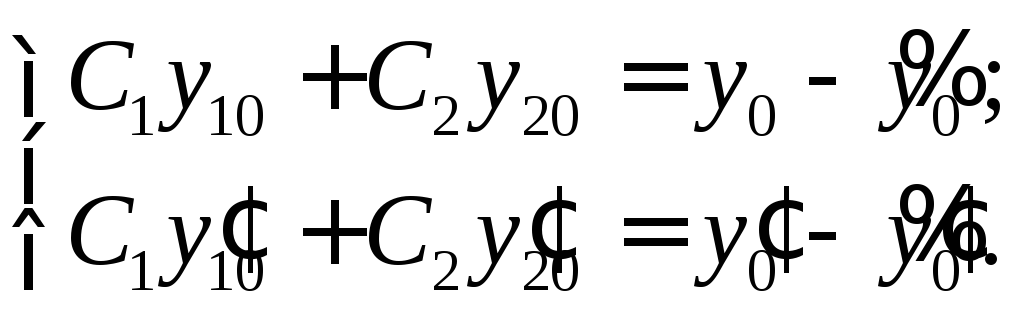 (9)
(9)
Система (9) является
линейной системой для определения
![]() и
и![]() с определителем
с определителем
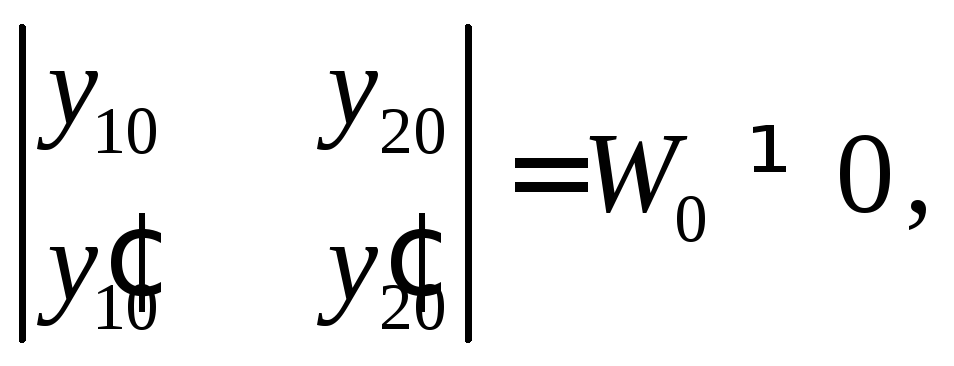
так как
![]() и
и![]()
ЛНЗ решения уравнения (7). Из решения
системы (9) определяем
ЛНЗ решения уравнения (7). Из решения
системы (9) определяем
![]() и
и![]() .
Таким образом,
.
Таким образом,![]() является общим решением уравнения (6).
является общим решением уравнения (6).
Замечание.
Если
![]()
функции от х,
то не существует общих методов
интегрирования уравнений (6) и (7).
Рассмотрим случай, когда известно общее
решение соответствующего однородного
уравнения.
функции от х,
то не существует общих методов
интегрирования уравнений (6) и (7).
Рассмотрим случай, когда известно общее
решение соответствующего однородного
уравнения.
