
- •Дифференциальные уравнения Лекция № 37. Тема 1 : Введение
- •1.1. Задачи, приводящие к дифференциальным уравнениям
- •1.2. Определение дифференциального уравнения
- •Тема 2: Дифференциальные уравнения первого порядка
- •2.1. Общие понятия. Теорема существования и единственности
- •2.2. Уравнения с разделяющимися переменными
- •Лекция № 38
- •2.3. Однородные уравнения
- •Лекция № 39. Тема 3 : ду высших порядков
- •3.1. Определение ду п-го порядка
- •3.2. Уравнения, допускающие понижение порядка
- •4.2. Теорема о структуре общего решения лоду-2
- •Лекция № 40
- •4.3. Лоду-2 с постоянными коэффициентами
- •4.4. Линейные неоднородные дифференциальные уравнения второго порядка
- •4.5. Метод вариации произвольных постоянных (метод Лагранжа)
Лекция № 39. Тема 3 : ду высших порядков
3.1. Определение ду п-го порядка
Общий вид дифференциального уравнения п-го порядка (ДУ-п):
![]() ,
(1)
,
(1)
или разрешенного относительно старшей производной:
![]() .
.
Дляпоискачастногорешениянеобходимо задать начальные условия:
![]() .
(2)
.
(2)
Определение 1.
Общим решением или интегралом уравнения
(1) назы-вается функция
![]() или
или![]() соответст-венно, которая:
соответст-венно, которая:
1. Удовлетворяет
уравнению при любых значениях произвольных
посто-янных
![]() .
.
2. При любых заданных
начальных условиях (2) из области
определения можно найти такие
![]() ,
что функция
,
что функция![]() или
или![]() соответственно будет удовлетворять
условиям (2).
соответственно будет удовлетворять
условиям (2).
3.2. Уравнения, допускающие понижение порядка
3.2.1.
![]() .
.
Для нахождения решения данного уравнения необходимо проинтегри-ровать его п раз.
Пример 1.
Найти общее решение уравнения
![]() .
.
Проинтегрируем уравнение три раза:
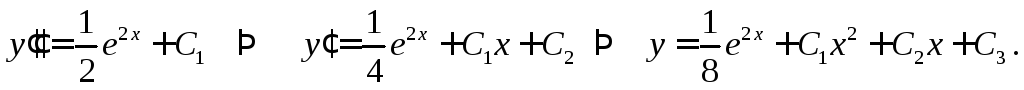
3.2.2.
![]() (нету).
(нету).
При помощи замены
![]() уравнение принимает вид
уравнение принимает вид
![]() .
.
Пример 2.
Найти общее решение уравнения
![]() .
.
После замены
![]() уравнение принимает вид
уравнение принимает вид
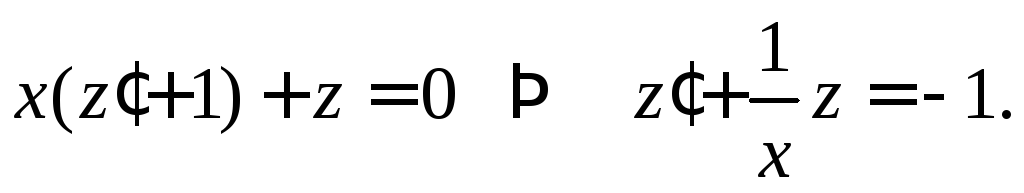
Это линейное
уравнение, поэтому используем
подстановку
![]()
Тогда получим
![]()
и
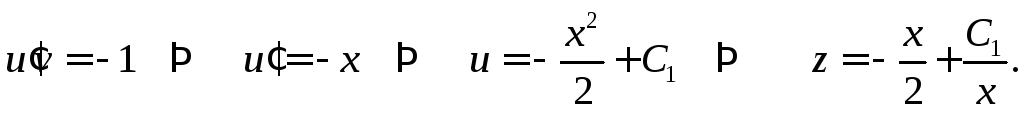
Так как
![]() ,
то
,
то
![]() .
.
Интегрируя, окончательно получаем
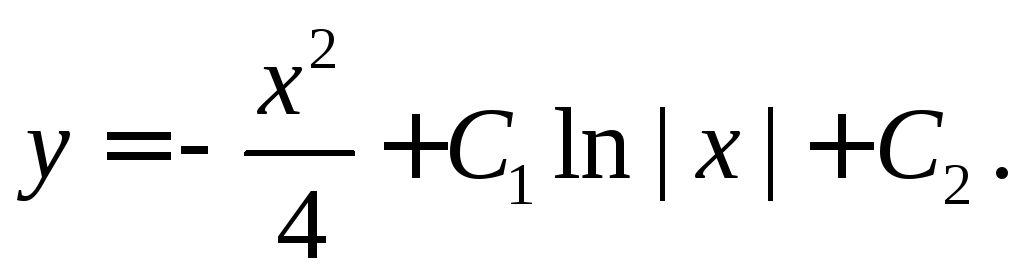
3.2.3.
![]() (нетх).
(нетх).
При помощи замены
![]() …
…
уравнение принимает вид
![]() .
.
Пример 3.
Решить задачу Коши
![]() .
.
После замены
![]() получим уравнение с разде-ляющимися
переменными:
получим уравнение с разде-ляющимися
переменными:
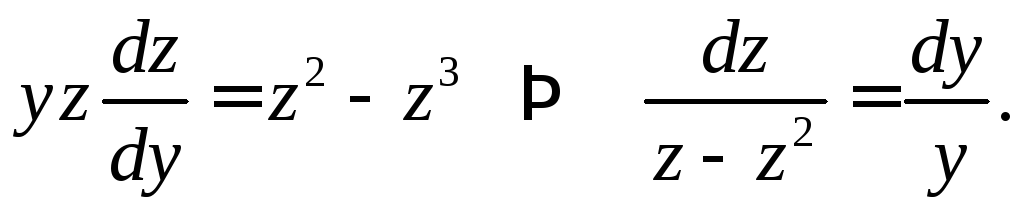
Проинтегрируем:
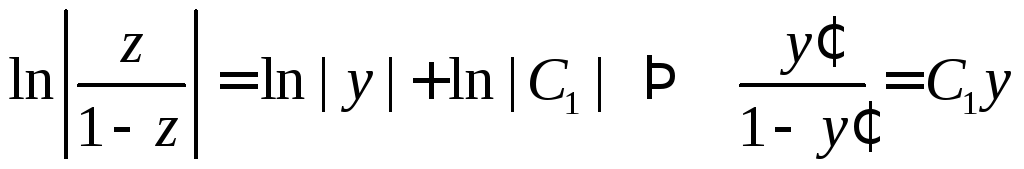 .
.
Воспользуемся начальными условиями
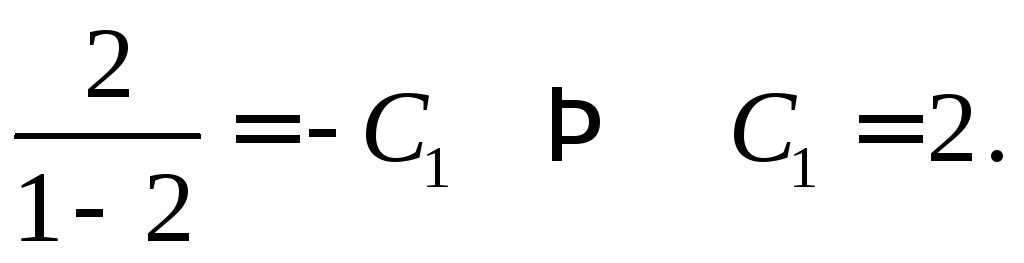
Разрешим уравнение
относительно
![]() и разделим переменные
и разделим переменные

Проинтегрируем

Из начальных
условий находим
![]() и, окончательно, получаем частное
решение
и, окончательно, получаем частное
решение
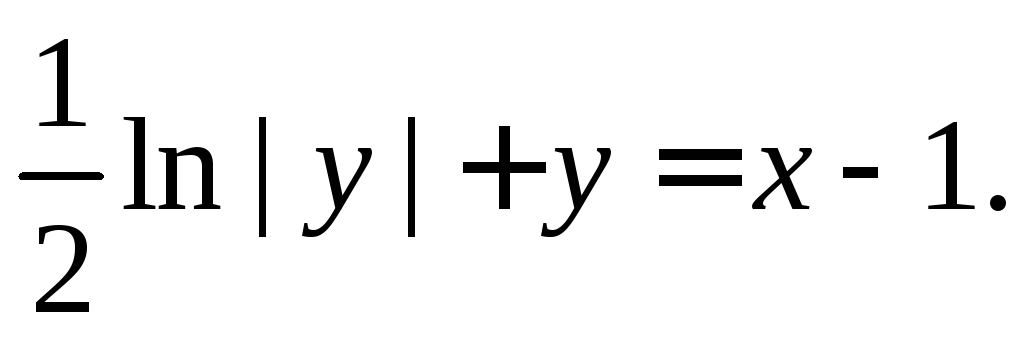
Тема 4 : Линейные дифференциальные уравнения второго порядка
4.1. Линейные однородные дифференциальные уравнения второго порядка (ЛОДУ-2). Определитель Вронского и его свойства
Общий вид
![]() ,
(3)
,
(3)
где
![]() и
и![]() непрерывные на некотором отрезке
непрерывные на некотором отрезке![]() функции.
функции.
Определение 2.
Функции
![]() и
и![]() называютсялинейно
зависи-мыми
(ЛЗ) на
называютсялинейно
зависи-мыми
(ЛЗ) на
![]() ,
если
,
если![]() ,
где, по крайней мере, одно из них отличное
от нуля, и для которых выполняется
равенство
,
где, по крайней мере, одно из них отличное
от нуля, и для которых выполняется
равенство![]() или, если
или, если![]() ,
то
,
то![]() ,
т.е.
,
т.е.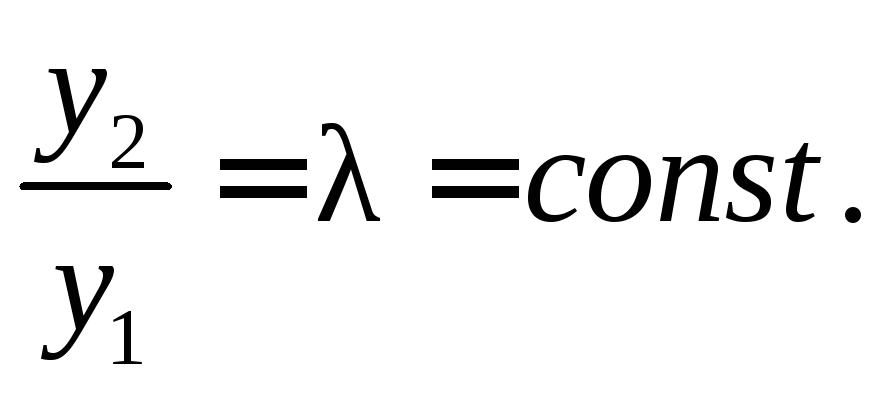
В противном случае,
функции
![]() и
и![]() называютсялинейно
независимыми
(ЛНЗ).
называютсялинейно
независимыми
(ЛНЗ).
Например, функции
![]() и
и![]()
ЛЗ, так как
ЛЗ, так как
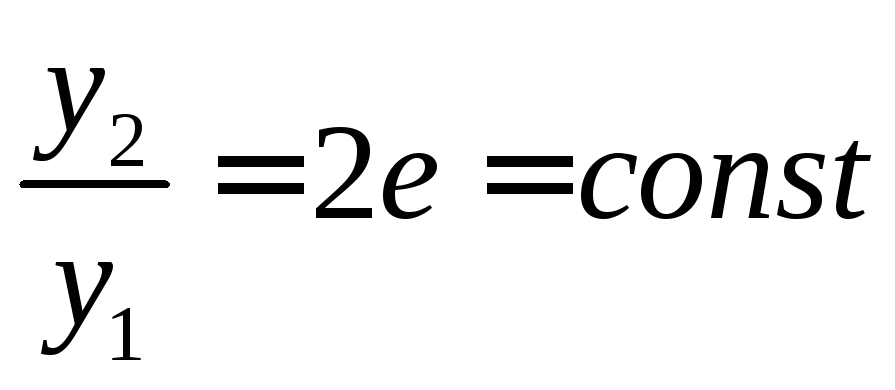 ,
а функции
,
а функции![]() и
и![]()
ЛНЗ, так как
ЛНЗ, так как
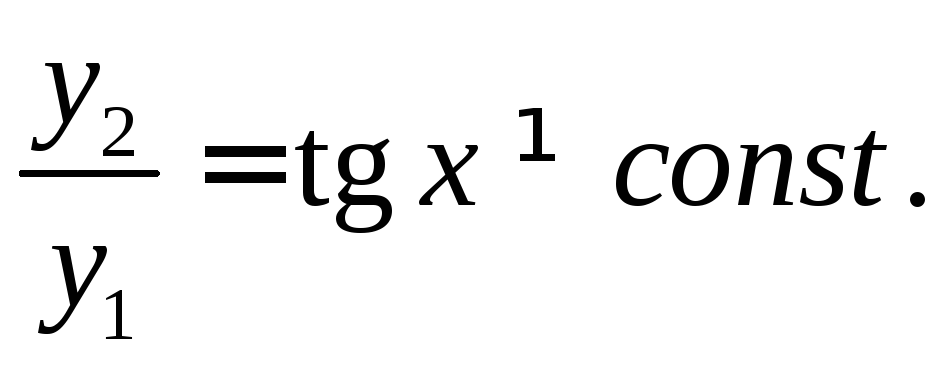
Для выяснения ЛЗ или ЛНЗ решений уравнения (3) используется определитель Вронского
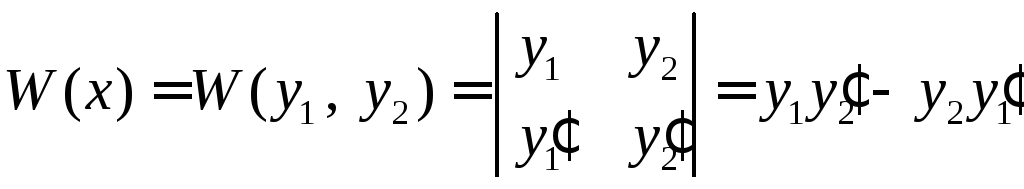 ,
,
что следует из теорем:
Теорема 1.
Если функции
![]() и
и![]() линейно зависимы (ЛЗ) на
линейно зависимы (ЛЗ) на![]() ,
то определитель Вронского
,
то определитель Вронского![]() .
.
Так как
![]() ,
то
,
то
![]() .
.
Теорема 2.
Если определитель Вронского, составленный
из решений уравнения (3), при некотором
![]() отличен от нуля, т.е.
отличен от нуля, т.е.![]() то
то![]()
Так как
![]() и
и![]() решения уравнения (3), то
решения уравнения (3), то
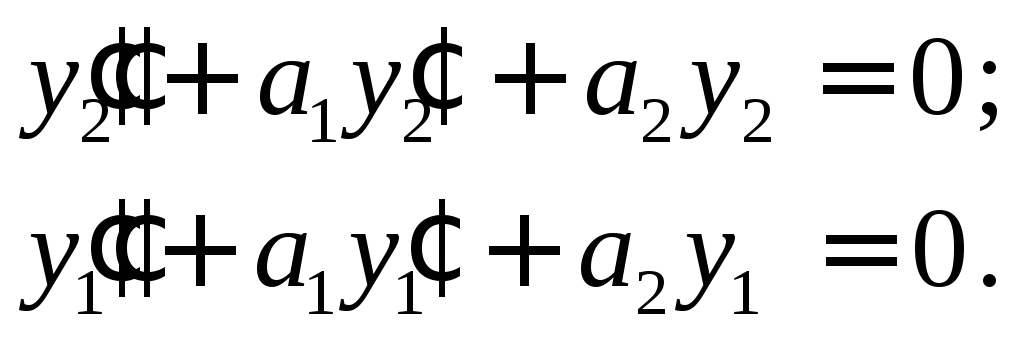
Первое равенство
умножим на
![]() ,
второе на
,
второе на![]() и сложим полученные результаты. С
учётом, что
и сложим полученные результаты. С
учётом, что
![]() ,
,
получим уравнение с разделяющимися переменными
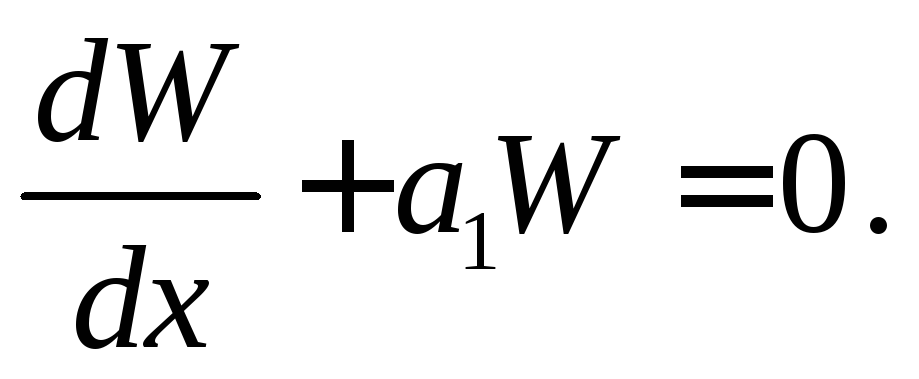
Найдём его решение,
удовлетворяющее начальному условию
![]()
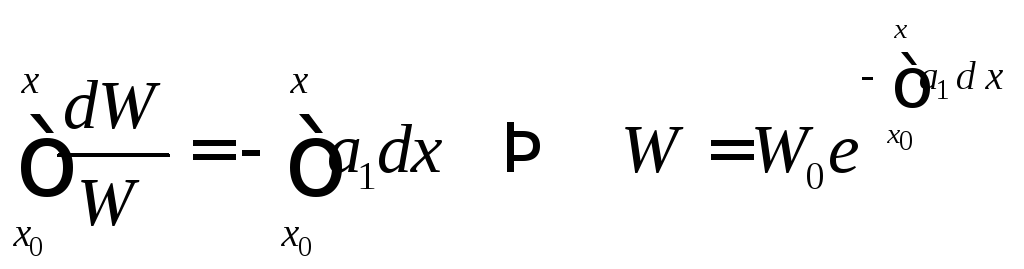 (4)
(4)
или
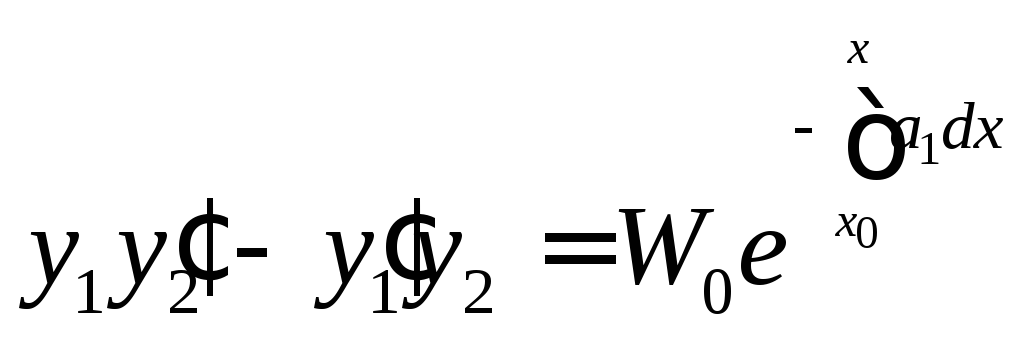 .
.
Формула (4) называется формулой Лиувилля. Из неё видно, что если
![]() то
то
![]() .
.
Замечание 1.
Из формулы (4) также следует, что если
при некотором.
![]()
Замечание 2.
По формуле Лиувилля, зная одно из решений
ЛОДУ-2, можно найти другое. Разделив
обе части равенства (4) на
![]() получим
получим
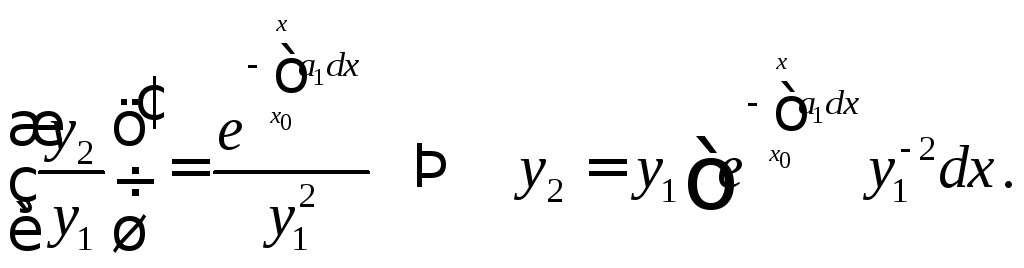
Теорема 3.
Если решения ЛОДУ-2 (3) ЛНЗ на
![]() ,
то
,
то![]() .
.
Предположим
обратное, т.е.
![]() при некотором
при некотором![]() .
Тогда по теореме2
.
Тогда по теореме2
![]() .
Предположим, что
.
Предположим, что![]() (в противном случае определитель
Вронского тождественно равен нулю),
тогда имеем равенство
(в противном случае определитель
Вронского тождественно равен нулю),
тогда имеем равенство

т.е. функции
![]() и
и![]() линейно зависимы. Полученное противоречие
доказывает теорему.
линейно зависимы. Полученное противоречие
доказывает теорему.
