Лекция № 6. Тема 3 : Векторное произведение

3.1. Векторное произведение двух векторов и его основные свойства

Определение 1. Векторным произведением двух векторов иназывается вектор, удовлетворяющий следующим условиям:

1.

2. вектор перпендикулярен векторами.

3. вектора образуют правую тройку, т.е. из конца третьего векторакратчайший поворот от векторако второму векторувиден против часовой стрелки.

В противном случае тройка векторов называется левой.

а) правая б) левая

Обозначается векторное произведение: или

Из определения векторного произведения следуют его свойства и геометрический смысл:

Модуль векторного произведения численно равен площади паралле-лограмма, построенного на этих векторах.

Основные свойства векторного произведения:

1.  векторное произведение антикоммутативно.

2. , где, еслииколлинеарные или по крайней мере один из сомножителей является нулевым вектором.

3.

4.

Замечание 1. Тройка базисных векторов является правой.

3.2. Векторное произведение векторов, заданных своими координатами

Из определения векторного произведения следует, что:

(1)

Тогда с учетом формул (1) и свойств векторного произведения получаем

(2)

Пример 1. Заданы векторы иНайти площадь параллелограмма, построенного на этих векторах.

Исходя из геометрического смысла векторного произведения, получим

Тогда

Замечание 2. Площадь треугольника, построенного на векторах ибудет равна.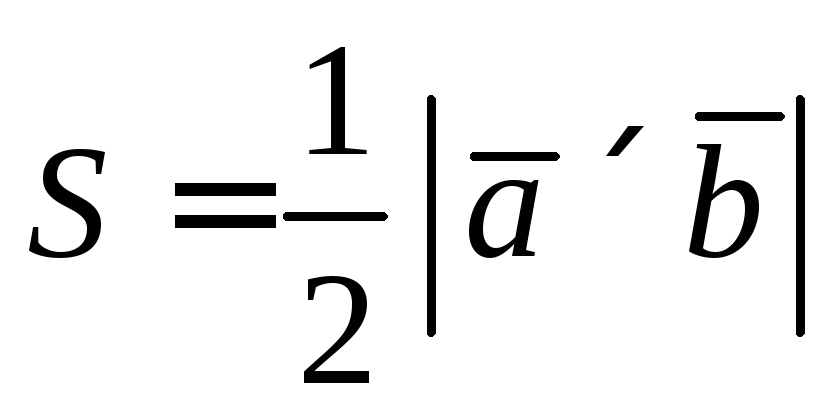

3.3.* Механический смысл векторного произведения

Если  радиус-вектор точки , к которой при-ложена сила, то момент этой силы относительно точкивычисляется по формуле

(3)

При этом моменты силы относительно координатных осей.z

Рассмотрим задачу из механики: 3 M

В точке приложена сила

. Требуется найти моменты

этой силы относительно координатных осей. 2 y

По формуле (3) получаем х

Полезно отметить тот факт, что значения этих моментов совпадают со школьным определением – “Момент равен произведению силы на плечо“. См. рисунок!

Тема 4 : Смешанное произведение

4.1. Смешанное произведение и его основные свойства

Определение 2. Векторно–скалярное произведение называется смешанным и обозначается

Рассмотрим его геометрический смысл.

Построим параллелепипед на векторах

Его объем равен в

его основании лежит параллелограмм с h

площадью

Его высота поэтому имеем

(4)

Знак в выражении совпадает со знакоми поэтому смешанное произведение положительно, если вектораобразуют правую тройку.

Таким образом, приходим к следующему правилу:

Смешанное произведение некомпланарных векторов по модулю равно объёму параллелепипеда, построенного на этих векторах. Оно поло-жительно, если тройка векторов правая и отрицательно, если левая.

Рассмотрим основные свойства смешанного произведения:

1. Если смешанное произведение равно нулю, то векторы компланарны.

Верно и обратное, т.е., если сомножители компланарны, то смешанное произведение равно нулю.

Равенство возможно в следую-щих случаях:

а) хотя бы один из векторов является нулевым, то векторы компланарны;

б) иколлинеарны компланарны;

в)  компланарны.

Аналогично доказывается обратное утверждение.

2. , т.е. при циклической перестановке сомножителей смешанное произведение знак не меняется. Это следует из того, что в данном случае ориентация тройки этих векторов сохраняется. В остальных случаях перестановки сомножителей ориентация векторов меняется и тогда

3. где А и В кон-станты.

Это свойство следует из свойств векторного и скалярного произве-дений.