Лекция № 2. Тема 2 : Системы линейных алгебраических уравнений

2.1. Правило Крамера

Рассмотрим систему трёх линейных алгебраических уравнений, когда число неизвестных равно числу уравнений, т.е. систему вида

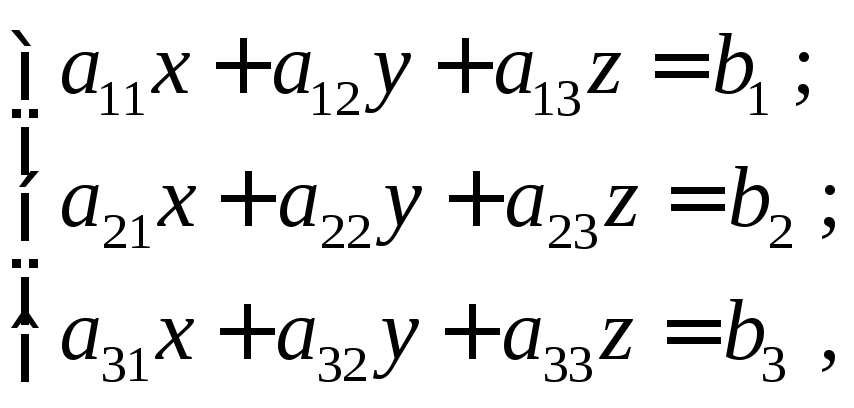(1)

где  коэффициенты системы,  свободные члены , неизвестные.

Будем считать, что определитель системы, составленный из коэффи-циентов системы (главный определитель), отличен от нуля, т.е.

Предположим, что система (1) совместна, т.е. имеет решение. Тогда умножим первое уравнение системы на , второе – на, третье – наи сложим полученные выражения

(2)

Первое выражение в скобках в левой части полученного соотношения (2) представляет собой разложение главного определителя системы по элементам первого столбца. Остальные выражения в скобках равны нулю, так как представляют собой разложение определителя, имеющего два одинаковых столбца (см. свойство4). Например,

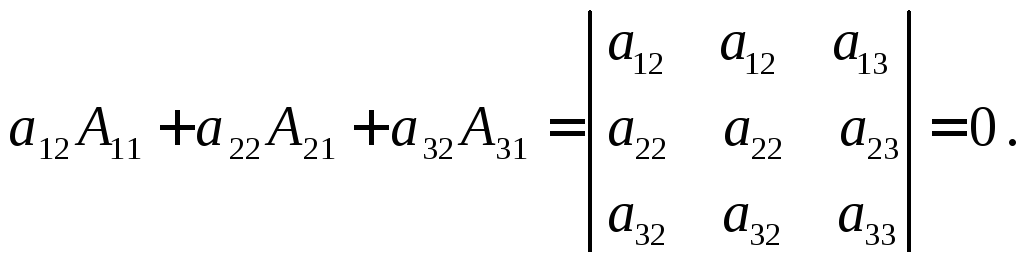
Тогда из выражения (2) получаем , где

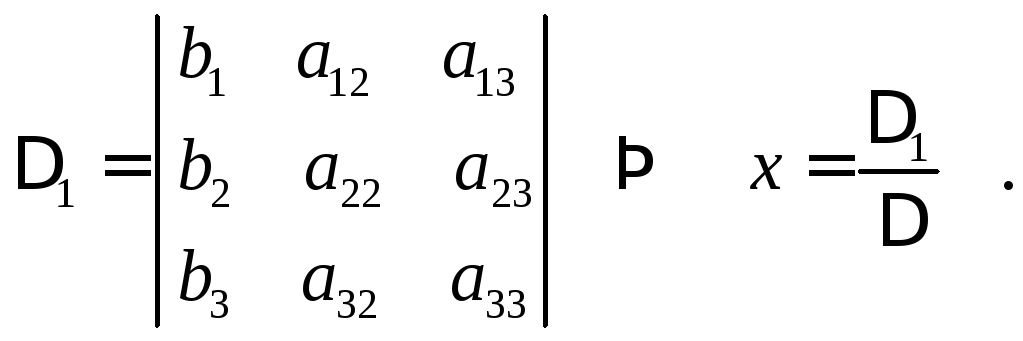
Аналогично можно получить

(3)

где

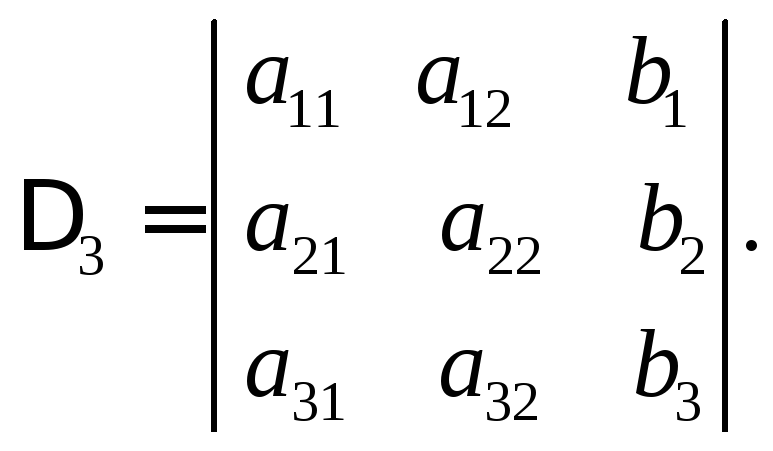
Определители называютсявспомогательными опреде-лителями системы (1).

Покажем теперь, что полученные значения неизвестных (3) на самом деле удовлетворяют системе уравнений (1).

Подставляя выражения (3) в систему (1), получим на примере первого уравнения

Аналогично можно показать и для двух оставшихся уравнений системы.

Таким образом, получаем следующий результат (правило Крамера).

Теорема. Система уравнений (1) с главным определителем имеет единственное решение, определяемое по формулам

где определители получаются из главного определителясистемы уравнений заменой соответствующего столбца на столбец свобод-ных членов.

Замечание 1. Для системы линейных однородных уравнений

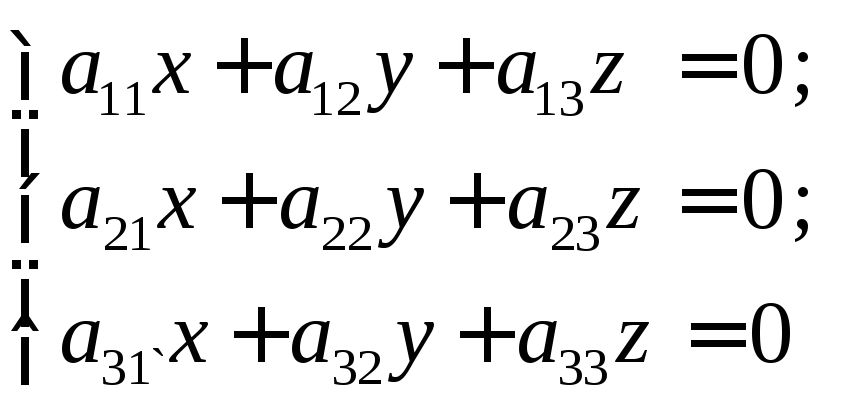(4)

все и тогда, если, то система (4) имеет единст-венное нулевое решение Отсюда следует: если система (4) обладает ненулевым решением, то её определитель равен нулю.

Замечание 2. Если же главный определитель системы (1) , тогда возможны следующие два случая:

1. Система несовместна, если, по крайней мере, один из вспомога-тельных определителей отличен от нуля;

2. Если же все определители системы равны нулю, то система либо имеет бесконечное множество решений, что возможно из равенств

либо такая система несовместна, например, в системе уравнений

все определители равнынулю, носистеманесовместна, чтоследуетиз ее вида. В этом случае для решения системы уравнений более целесообразно применить метод Гаусса, который будет рассмотрен далее.

Замечание 3. Правило Крамера справедливо для любого числа уравнений системы, т.е. системы вида

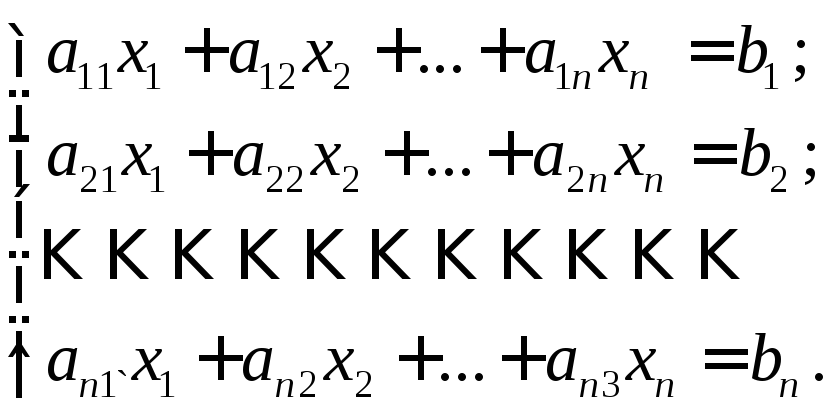
Здесь, если то

Пример 1. Используя правило Крамера, решить систему уравнений

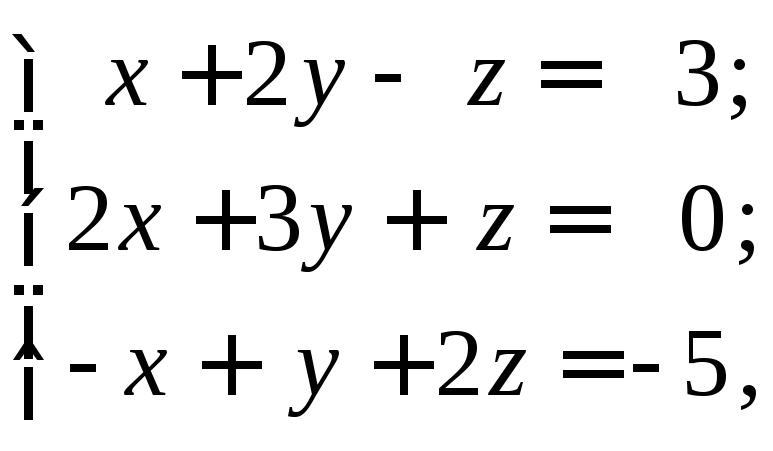
Здесь

откуда получаем

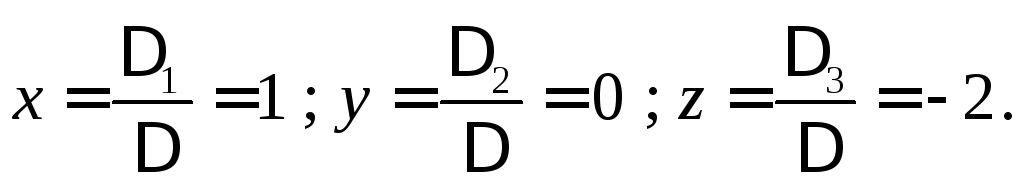
2.2. Метод Гаусса (метод последовательного исключения неизвестных)

Рассмотрим ту же систему уравнений (1). Пусть коэффициент , чего всегда можно достигнуть, переставляя уравнения системы или меняя нумерацию неизвестных. Первое уравнение системы (1) умножим наи сложим со вторым. Затем первое уравнение умножим наи сложим с третьим, тогда получим

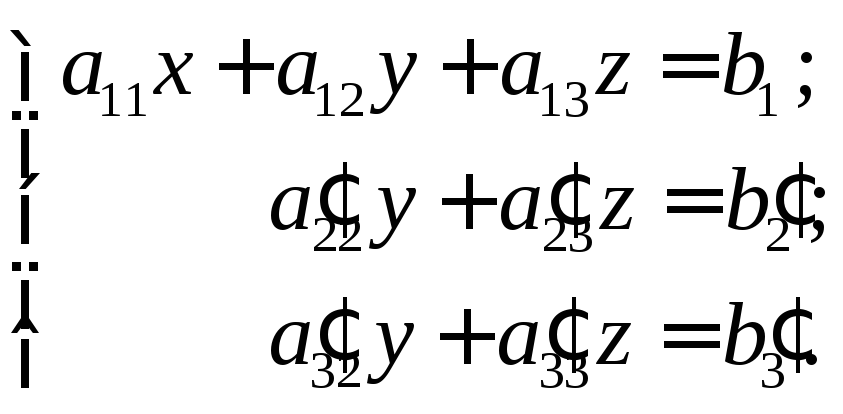(5)

Здесь  новые значения коэффициентов, полу-ченные после таких преобразований. Пусть , чего можно достигнуть, переставляя два последних уравнения системы. В противном случае, т.е. когда, сразу определяем неизвестнуюz, или получаем несов-местную систему. При таком условии второе уравнение системы (5) умно-жим на и сложим с третьим уравнением, тогда получим

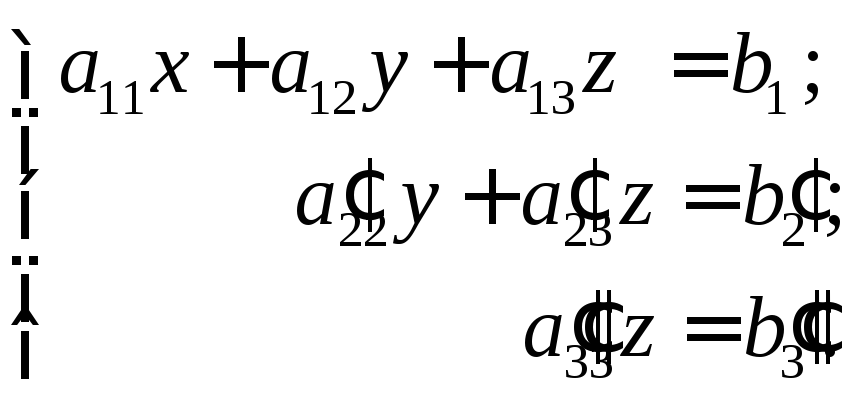(6)

В системе уравнений (6)  новые значения коэффициентов и здесь возможны следующие случаи:

1. Затем найденное значениеz подставляем во второе уравнение системы (6) и определяем у. Из первого уравнения, уже зная у и z, находим х.

2. а. Тогда система (6) решений не имеет, т.е. система несовместна.

3. и. В этом случае система (6) принимает вид

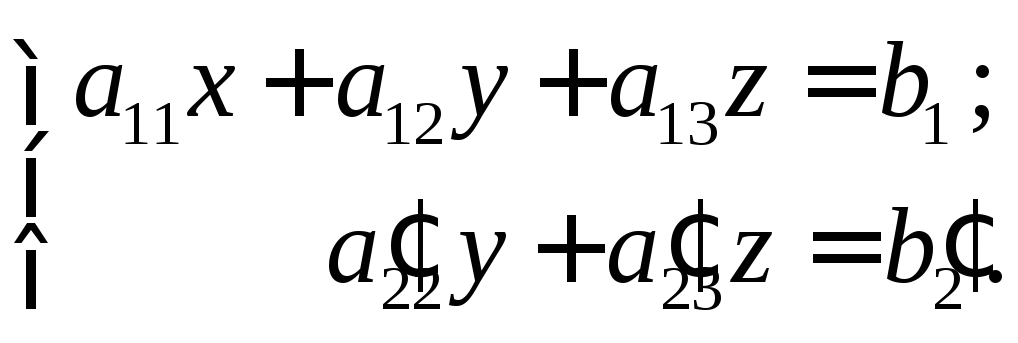(7)

Число уравнений в системе (7) меньше числа неизвестных. Оставим два неизвестных слева, например, х и у, а z перенесем в правую часть системы уравнений (7) и будем считать его произвольным числом. Получим

(8)

Из системы (8) х и у выражаются через z и система имеет беско-нечное множество решений.

Пример 2. Систему уравнений из примера 1 решить методом Гаусса

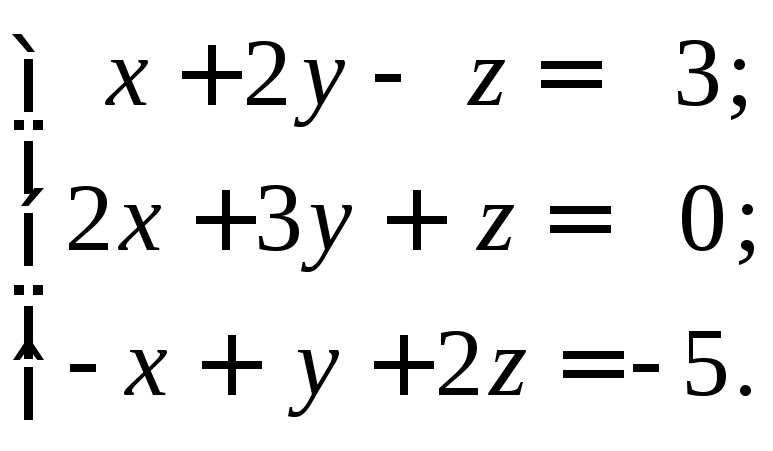
Первое уравнение умножим на 2 и сложим со вторым уравнением, затем первое уравнение сложим с третьим, получим

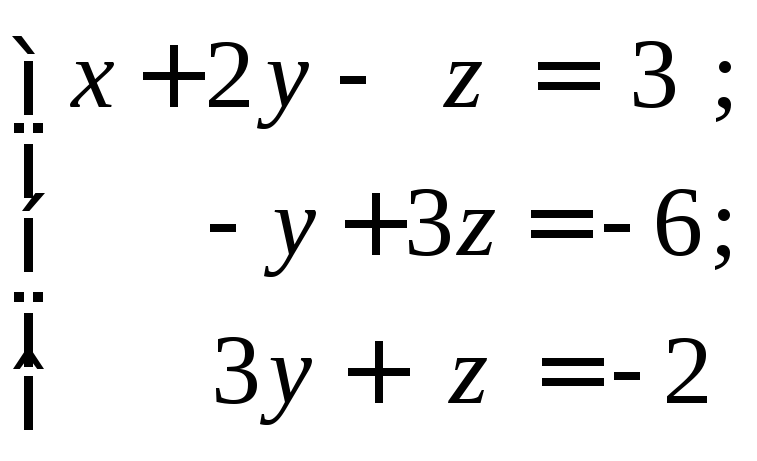или

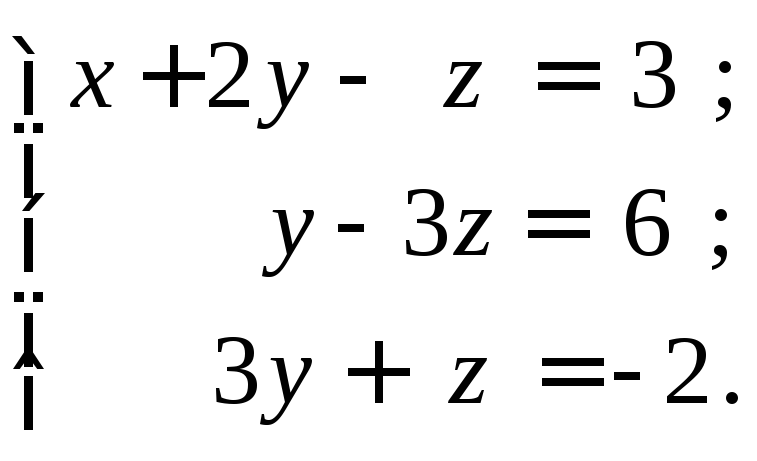
Второе уравнение умножим на 3 и сложим с третьим:

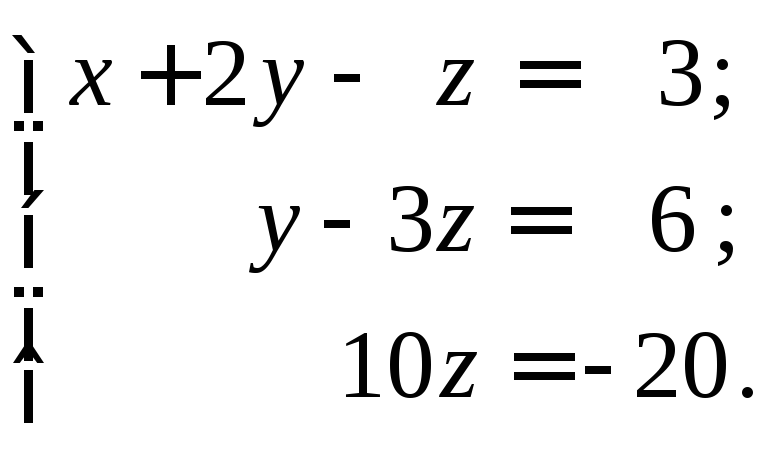
Из третьего уравнения получим, из второгои из пер-вого уравнения

Пример 3. Методом Гаусса решить систему однородных уравнений

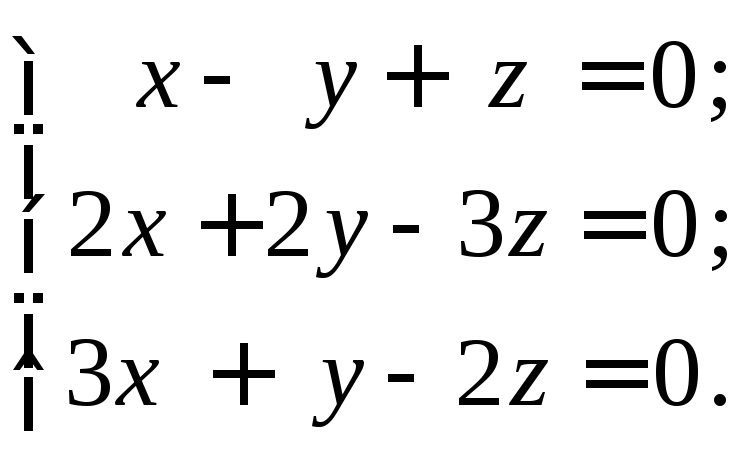
Первое уравнение умножим на 2 и сложим со вторым, затем первое уравнение умножим на 3 и сложим с третьим, получим

откуда

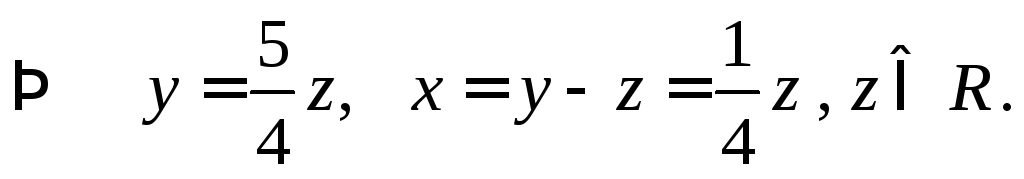
Система имеет бесконечное множество решений. Поэтому в этом случае (см. замечание 1) определитель данной системы уравнений должен быть равен нулю. Проверьте!