Лекция № 5.

1.4. Способы задания векторов

Вектор может быть задан следующими способами:

1. Координатами вектора

2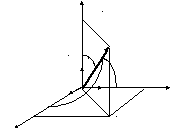. Координатами начальнойz

и конечной точек.

3. Модулем вектора и углами,M

которые он образует с координатными осями.

При этом значения

называются направляющими косинусами. O y

Между этими способами задания a_z

векторов существует определённая связь. a_x

Например, переход от (2) к (1) x a_y

осуществляется следующим образом:

так как, тоz A

.

Переход от (3) к (1) и наоборот

осуществляется по формулам: B

x O y

1.5. Деление отрезка в заданном отношении

Рассмотрим следующую задачу: даны две точки и. Требуется найти точку такую, что отно-шениеz А

Построим векторы: М

Из условия коллинеарности векторов

и имеемВ

Полученное равенство представим в

координатной форме х О у

или окончательно

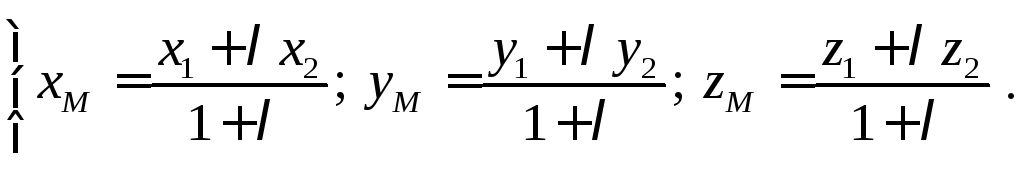(1)

Замечание 1. Из формул (1) следует частный случай деления отрезка пополам

Пример 1. Треугольник задан координатами своих вершин Найти его центр тяжести. z В

Известно, что центр тяжести треугольника

лежит на пересечении его медиан и, если

точка К  середина стороны ВС, то по А М К

свойству медиан 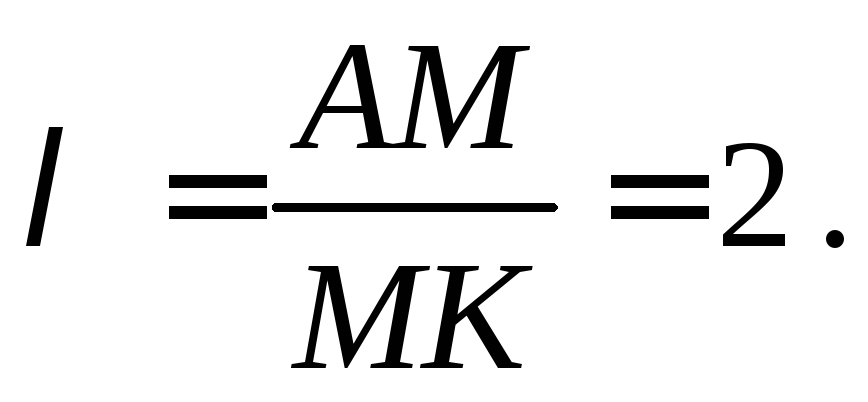у

Определим вначале координаты х С

точки К:

далее по формулам (1) получим координаты точки М:

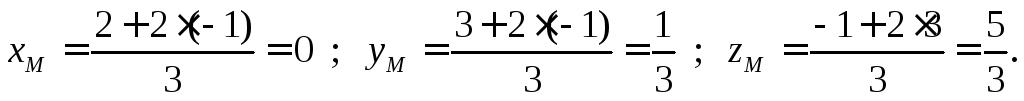
Тема 2: Скалярное произведение

2.1. Скалярное произведение двух векторов и его основные свойства

Определение. Скалярным произведением двух векторов иназывается число, равное произведению модулей этих векторов на косинус угла между ними и обозначается

(2)

Замечание 2. Формулу (2) можно представить в другой форме

(3)

откуда получим

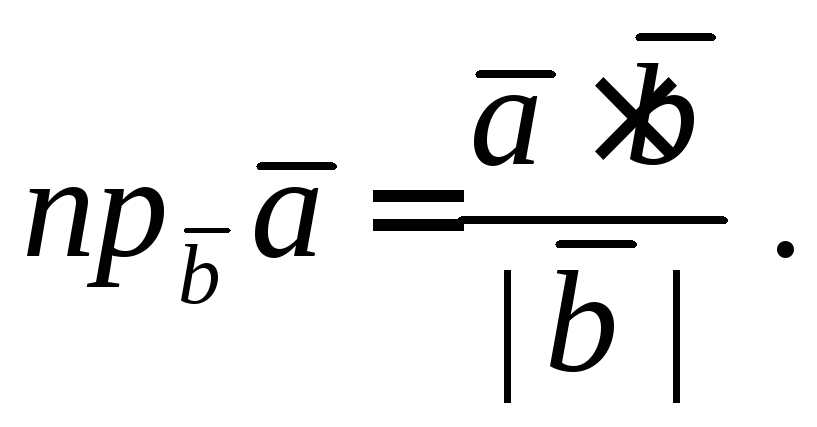
Рассмотрим механический смысл скалярного произведения. Если  постоянная сила, а  вектор перемещения, то  работа силы на перемещении

Из определения скалярного произведения следуют его свойства:

1.  скалярное произведение коммутативно.

2. , если векторыиперпендикулярны (ортогональны), или хотя бы один из них является нулевым вектором.

3.

Если воспользоваться замечанием 1 из лекции 4 и формулами (3), то легко доказать следующее свойство:

4.

Таким образом, операции со скалярным произведением аналогичны операциям с многочленами.

2.2. Скалярное произведение векторов, заданных координатами

Из определения и свойства (1) скалярного произведения следуют формулы: .

Аналогично получаем:

Тогда, если

то

(4)

2.3. Длина вектора. Угол между двумя векторами.

Направляющие косинусы

По формулам (2) и (4) получаем

откуда

(5)

Из определения скалярного произведения и формул (4), (5) следует

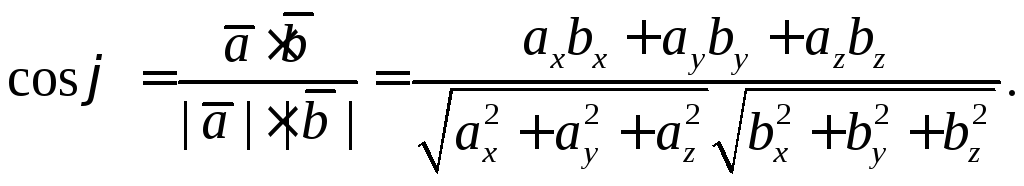
(6)

Аналогично получим

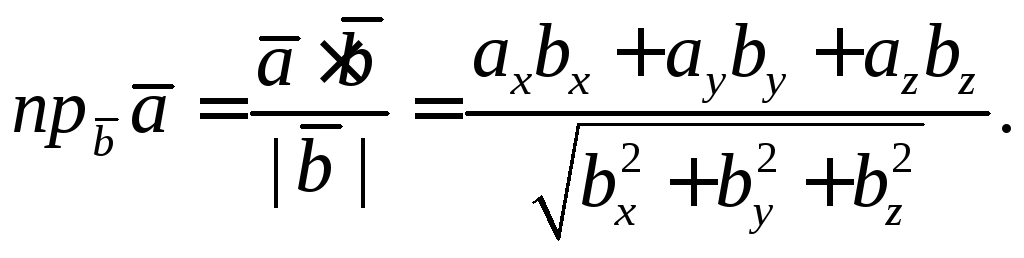(7)

Если в формуле (7) положить , то найдем

.

Аналогично можно получить выражения для оставшихся двух направ-ляющих косинусов

; . (8)

Замечание 3. Формулу (5) для модуля вектора можно было получить, исходя из геометрического смысла координат вектора, используя теоре-му Пифагора.

Замечание 4. Из выражений (8) для направляющих косинусов следует их основное свойство

Пример 2. Даны два вектора Найти их скалярное произведение и угол между ними.

По формулам (5) и (7) получаем

Пример 3*. Найти координаты единичного вектора, который перпенди-кулярен вектору и образует угол с вектором

Из свойства направляющих косинусов следует, что координаты еди-ничного вектора равны значениям соответствующих направляющих косинусов и поэтому из условия задачи получаем следующую систему уравнений

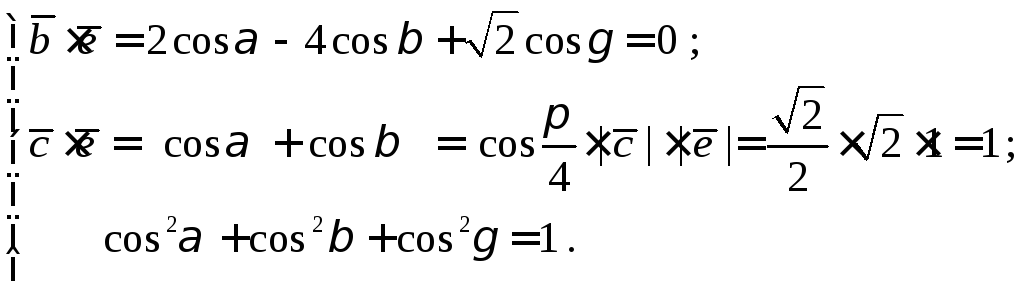
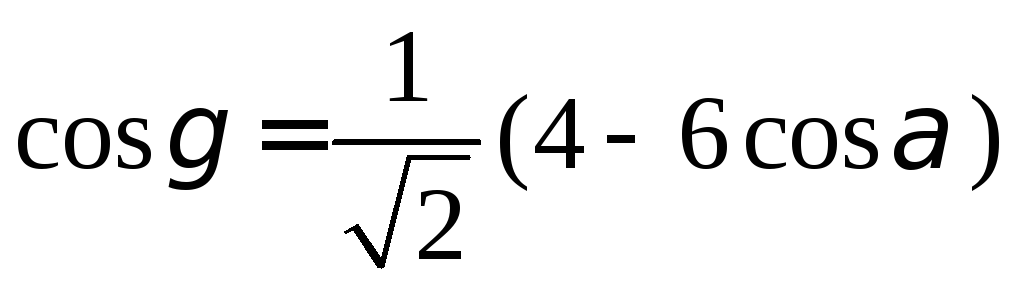Из второго уравнения системы получаем Тогдареньонний 000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 из первого уравнения имеем . Если полученные выражения подставить в третье уравнение системы, то приходим к квадратному уравнению

Из этого уравнения и. Тогда окончательно нахо-дим два единичных вектора, удовлет-воряющих условию задачи.