II о замене переменной в несобственных интегралах

В несобственных интеграла с одной особой точкой – конечной или бес-конечной, – которая к тому же является одним из пределов интегрирования, возможна замена переменной , где– монотонная непрерывно-дифференцируемая функция.

Примеры. 3. . Особая точка.

Замена: – монотонно возрастающая. Необходимые вычисления:

, ,,.

Имеем

.

Обратите внимание на интересную особенность: исходный интеграл 2-го рода после замены превратился в несобственный интеграл 1-го рода. Он сходится по признаку Дирихле: функция – монотонно стремится к нулю,– имеет ограниченную первообразную.

4. . Особая точка. Замена:,,,. Имеем:

…

Это еще более интересный случай: несобственный интеграл после замены превращается в обычный определенный.

§6. Гамма-функция Эйлера

Если функцию двух переменных проинтегрировать в некото-ром промежутке по одной из переменных, например, по, то полученный определенный или несобственный интеграл будет являться функцией другой переменной. Такие интегралы называют интегралами, зависящими от параметра.

Гамма-функция Эйлера – это несобственный интеграл вида

.

Эта функция, после элементарных, является одной из важнейших для математического анализа и его приложений.

Если , то интеграл, который определяет функцию, имеет две особые точки:и. Разобьем этот интеграл на сумму двух:

.

Известно, что при. Значит, для достаточно больших значенийимеет место неравенство. Пусть, тогда для подынтегральной функции в интеграле(1-го рода) будем иметь:

.

Но интеграл сходится как эталонный, следовательно, и интегралсходится, причем для любого.

Для той же функции , но в интеграле(2-го рода), приимеем:

.

Интеграл , а с ним и интеграл, сходится при, т.е. при.

Итак, окончательно, гамма-функция определена для.

Выведем рекуррентную формулу для функции . Заметим, что интеграл, определяющий, – 1-го рода. Имеем:

.

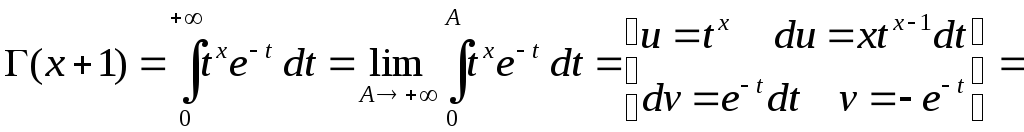
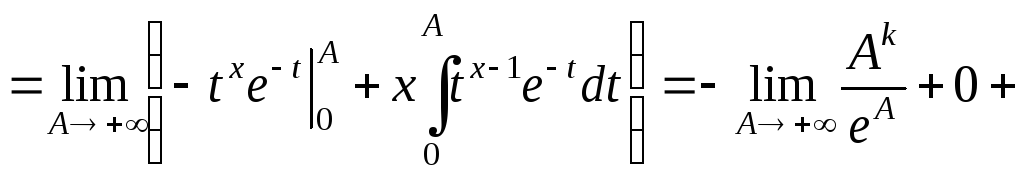
Кроме того,

.

Итак, и. Нетрудно заметить, что дляТаким образом, функцияявляется обобщением (на область любых) факториала.