
- •§1. Несобственные интегралы 1-го рода
- •I Определение
- •II Формула Ньютона – Лейбница для несобственного интеграла первого рода
- •II Интегралы от знакопеременных функций
- •§3. Несобственные интегралы 2го рода
- •I Одно свойство определенного интеграла
- •II Определения
- •III Формула Ньютона-Лейбница для несобственного интеграла 2-го рода
- •§4. Признаки сходимости несобственного интеграла 2-го рода
- •§5. Замечания к теме
- •I Об интегралах смешанного типа
- •II о замене переменной в несобственных интегралах
- •§6. Гамма-функция Эйлера
III Формула Ньютона-Лейбница для несобственного интеграла 2-го рода
Примем без доказательства теорему, которая упрощает вычисление несобственных интегралов 2-го рода.
Теорема
1.
Пусть функция
![]() имеет на отрезке
имеет на отрезке![]() одну или несколько особых точек и пусть
одну или несколько особых точек и пусть![]() – её первообразная, т.е.
– её первообразная, т.е.![]() всюду, за исключением особых точек. Если
эта первообразная непрерывна и в этих
особых точках, то имеет место формула
всюду, за исключением особых точек. Если
эта первообразная непрерывна и в этих
особых точках, то имеет место формула
![]() .
.
Примеры.
2.
![]() .
.
3.

4.
![]() .
Найдем первообразную:
.
Найдем первообразную:
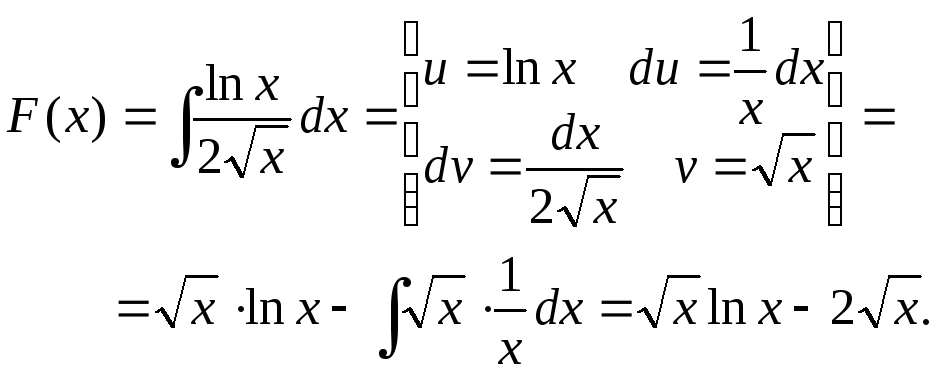
В
нуле первообразная не определенна,
однако
![]() .
Положив
.
Положив![]() ,
мы получим непрерывную на
,
мы получим непрерывную на![]() первообразную, поэтому
первообразную, поэтому
![]() .
.
§4. Признаки сходимости несобственного интеграла 2-го рода
Эти признаки совершенно аналогичны признакам сходимости для несобственного интеграла 1-го рода. Приведем лишь их формулировки.
Теорема
1
(1-й признак сравнения). Пусть функции
![]() и
и![]() непрерывны на
непрерывны на![]() и
и![]() – их общая особая точка. Если они
удовлетворяют условию
– их общая особая точка. Если они
удовлетворяют условию![]() ,
то:
,
то:
1)
из сходимости интеграла от функции
![]() следует сходимость
следует сходимость![]() интеграла
от функции
интеграла
от функции![]() ;
;
2)
из расходимости интеграла от функции
![]() следует расходимость
следует расходимость![]() интеграла
от функции
интеграла
от функции![]() .
.
Теорема
2
(2-й признак сравнения). Пусть функции
![]() и
и![]() непрерывны и неотрицательны на
непрерывны и неотрицательны на![]() и
и![]() – их общая особая точка. Если при
– их общая особая точка. Если при![]() эти функции эквивалентны, то несобственные
интегралы
эти функции эквивалентны, то несобственные
интегралы
![]() и
и
![]()
сходятся или расходятся одновременно.
В качестве эталонного интеграла 2-го рода берут интеграл вида
![]() ,
,
который
сходится при
![]() ,
и расходится при
,
и расходится при
![]() .
.
Примеры.
1.
![]() .
.
При
![]() (0
– особая точка)
(0
– особая точка)
![]() .
Кроме того
.
Кроме того![]() на
на![]() .
Т.к. интеграл
.
Т.к. интеграл
![]()
расходится, то и данный интеграл также расходится.
2.
![]() .
Особая точка:
.
Особая точка:![]() .
.
Прежде всего, разложим подкоренное выражение на множители:
![]()
![]() .
.
Теперь
нетрудно получить при
![]() оценку
оценку
![]()
=![]() .
.
Интеграл
![]() сходится как эталонный, следовательно
сходится и данный интеграл.
сходится как эталонный, следовательно
сходится и данный интеграл.
Теорема
3
(признак абсолютной сходимости). Если
сходится интеграл
![]() ,
то сходится и интеграл
,
то сходится и интеграл![]() (такую его сходимость называ-ют
абсолютной).
(такую его сходимость называ-ют
абсолютной).
Пример
3.
![]() .
.
Рассмотрим
модуль подынтегральной функции при
![]() :
:
![]() .
.
Интеграл
![]() сходится как эталонный. Последовательно
применяя 2-й и 1-й признаки сравнения,
получим, что
сходится как эталонный. Последовательно
применяя 2-й и 1-й признаки сравнения,
получим, что![]() сходится. Значит, и исходный интеграл
сходится, причем абсолютно.
сходится. Значит, и исходный интеграл
сходится, причем абсолютно.
Пример
4.
![]() .
.
Если
к этому интегралу применить (незаконно!)
свойство линейности, то получим разность
двух несобственных расходящихся
интегралов. На самом же деле для
подынтегральной функции
![]() нетрудно получить эквивалент-ность в
особой точке
нетрудно получить эквивалент-ность в
особой точке![]() .
Действительно,
.
Действительно,
![]()
![]() .
.
Значит,
![]() при
при![]() ,
и исходный интеграл сходится вместе с
эталонным
,
и исходный интеграл сходится вместе с
эталонным![]() .
.
§5. Замечания к теме
I Об интегралах смешанного типа
Если
на бесконечном промежутке подынтегральная
функция имеет особые точки, то интеграл
разбивают на сумму отдельных интегралов,
пользуясь свойством аддитивности. При
этом необходимо, чтобы в каждом таком
интеграле была бы одна особая точка,
причем она являлась бы пределом
интегрирования. Для простоты и бесконечно
удаленную точку
![]() считаем особой.
считаем особой.
Примеры.
1.![]() .
Здесь две особые точки:
.
Здесь две особые точки:![]() и
и![]() .
Разобьем интеграл на сумму двух:
.
Разобьем интеграл на сумму двух:
![]() .
.
При
![]() :
:
![]() ,
где
,
где![]() .
Поэтому интеграл
.
Поэтому интеграл![]() сходится вместе с
сходится вместе с![]() для любого
для любого![]() .
Если же
.
Если же![]() ,
то
,
то![]() ,
где
,
где![]() .
Значит, интеграл
.
Значит, интеграл![]() сходится вместе с
сходится вместе с![]() лишь для
лишь для![]() .
Окончательный вывод: данный интеграл
сходится при
.
Окончательный вывод: данный интеграл
сходится при![]() .
.
2.
Исследуйте самостоятельно интеграл
![]() ,
разбив его на сумму таким образом:
,
разбив его на сумму таким образом:
![]() .
.
