II Интегралы от знакопеременных функций

Для таких функций наряду с интегралом рассматривают интеграл.

Определение. Несобственный интеграл называют абсолют-но сходящимся, если сходится интеграл.

Например, сходится абсолютно, ибо, интегралсходится, итакже сходится (1-й признак сравнения).

Теорема 4 (признак абсолютной сходимости). Если несобственный интеграл сходится абсолютно, то он просто сходится.

Доказательство. Рассмотрим еще две неотрицательные функции:

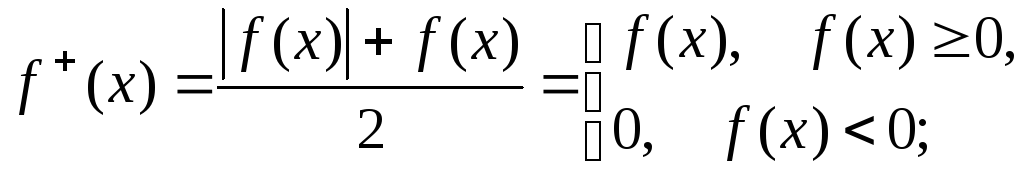
Нетрудно заметить, что , а. Введем обозначения:

Так как функции ,инеотрицательные, то функции,и – возрастающие. Кроме того, и. Далее, используя теорему 1, получим цепочку следований:

сходится абсолютно сходитсяфункцияограниченаиограничены

и сходятсясуществуют конечные пределыисуществует и конечен, т.е. данный интеграл сходится. Теорема доказана.

Заметим, что из сходимости не следует сходимость интеграла.

Пример 3.

Для модуля подынтегральной функции можно написать

Интеграл сходится как эталонный, сходится по одному из свойств, сходится по 2-му признаку сравнения,сходится по 1-му признаку сравнения, исходный интеграл сходится по признаку абсолютной сходимости.

Примем без доказательства еще один признак.

Теорема 5 (признак Дирихле). Пусть – непрерывная, дифферен-цируемая функция, которая монотонно стремится к 0 при , а функ-цияимеет ограниченную первообразную. Тогда интеграл

сходится.

Пример 4.

В этом интеграле , а. Условия признака Дирихле выполнены, следовательно, интеграл сходится.

Покажем, что интеграл от расходится. Проинтегрируем по промежуткуочевидное неравенство

:

(1)

Для интегралов в правой части неравенства найдем пределы при :

,

существует и конечен, ибо сходится по приз-наку Дирихле. Итак, левая часть неравенства (1) имеет пределом, следовательно и

.

Задачи. 1. Исследовать на сходимость интеграл .

2. Вычислить предел .

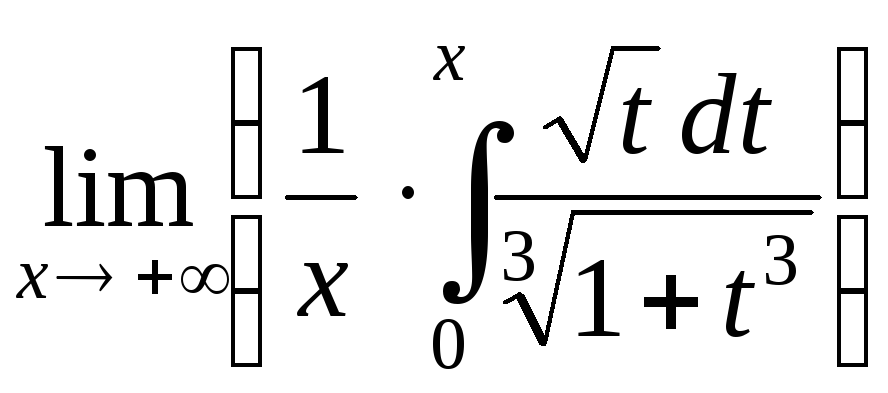§3. Несобственные интегралы 2го рода

I Одно свойство определенного интеграла

Известно, что, если функция непрерывна на отрезке, то интеграл с переменным верхним пределомявляется функ-цией дифференцируемой, следовательно, и непрерывной. Непрерывность же означает, например такое:. Другими словами:

.

(1)

Аналогично и для нижнего предела интегрирования:

.

(2)

Это свойство необходимо, например, в такой ситуации. Функция имеет в нуле разрыв, который можно устранить (ибо) и сделать её непрерывной на отрезке. Первообразную этой функции можно найти интегрированием по частям:. Но как воспользоваться формулой Ньютона – Лейбница для интеграла, ведь? Здесь используют свойство, выражаемое формулой (2):

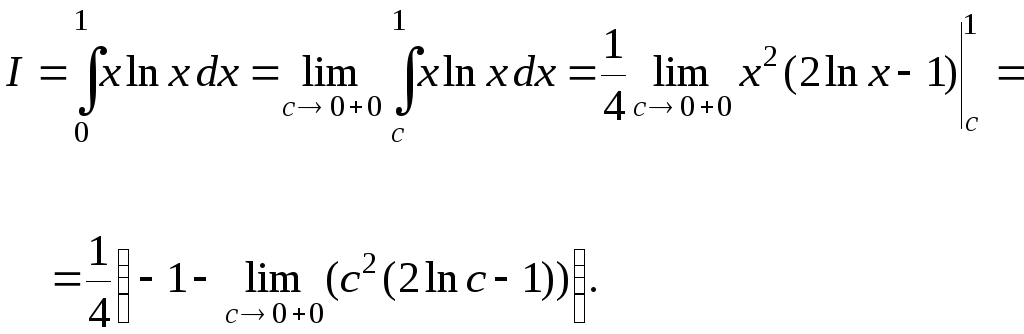
Раскрывая неопределенность типа , получим значение .

Именно формулы (1) и (2) берут в качестве определения интеграла от функции, которая не является ограниченной в точке или.

II Определения

Определение 1. Точку называют особой точкой функции, если в любой (сколь угодно малой) окрестности этой точки функция является неограниченной.

Например, если , то точка– особая.

Пусть функция непрерывна на промежуткеи точка– особая. Рассмотрим отрезок. Данная функция непрерывна на этом отрезке и, следовательно, существует,.

Определение 2. Конечный или бесконечный предел этого интеграла при называют несобственным интегралом 2^го рода от функции по промежуткуи обозначают символом. Если указанный предел конечен, несобственный интеграл называют сходящимся, в противном случае – расходящимся.

Итак, по определению, если – особая точка, то

.

Приведем определения и для других случаев расположения особых точек в промежутке интегрирования.

Определение 3. Если непрерывна наи– особая точка, то

.

Определение 4. Если непрерывна наии– особые точки, то

.

(3)

точка – произвольная из .

Определение 5. Если непрерывна наи–особая точка, то

.

(4)

К интегралам, стоящим в правых частях формул (3) и (4) применяем опреде-ления 2 и 3. При этом несобственный интеграл в левой части каждой из этих формул считают сходящимся, если только сходятся оба интеграла, которые стоят в правой части.

Пример 1. .

Подынтегральная функция имеет особую точку , расположенную внут-ри промежутка интегрирования, поэтому

.

Рассмотрим первый из этих интегралов:

Этот интеграл расходится, значит, расходится и данный интеграл .