1.4 Конкурентные сети

В предыдущем разделе на этапе обучения необходим “учитель”, который заранее выполняет классификацию образов, входящих в обучающую выборку и организует ее ввод в компьютер. Но в естественной биологической системе трудно себе представить наличие учителя и сам процесс обучения. Тем не менее, человек (и не только) способен выполнять классификацию без учителя, что дает основания думать, что объективно существуют алгоритмы обучения без учителя. В конкурентных сетях реализуется “обучение без учителя”. То есть в обучающей выборке для образов неизвестны правильные (желаемые) выходные реакции. Для реализации этого подхода необходимо решить две основные проблемы: 1) разработать методы разбиения образов на классы без учителя – этап обучения; 2) выработать правила отнесения текущего входного образа к некоторому классу – этап распознавания. Очевидно, разбиение на классы должно быть основано на использовании достаточно общих свойств классифицируемых объектов. В один класс должны попасть в некотором смысле похожие образы. При этом, как правило, используют компактность образов. В этом случае каждому классу в пространстве признаков соответствует обособленная группа точек. Тогда задача классификации сводится к разделению в многомерном пространстве на части множества точек. Процесс разбиения множества образов на классы называют кластеризацией. Визуально в двумерном (или трехмерном) пространстве разделение множества точек часто не представляет особых проблем, как это показано, например, на рис.8. Необходимо формализовать способ проведения границы между классами.

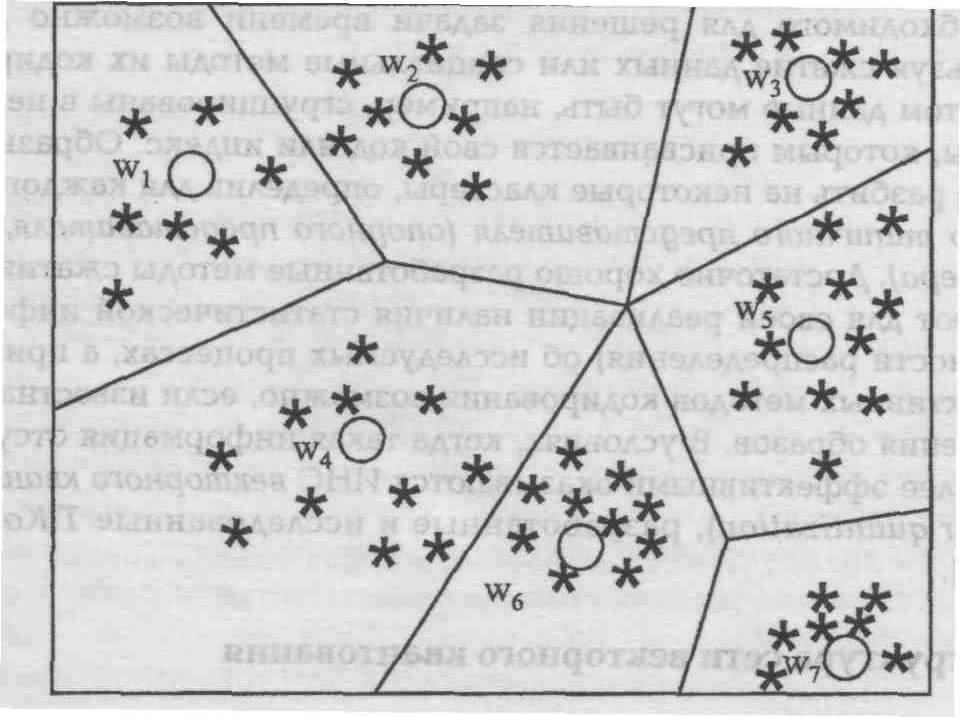
Рис. 8 Кластеризация данных

Архитектура сетей с конкурентным обучением достаточно проста. Большинство сетей этого типа имеют один слой нейронов, которые расположены в узлах некоторой решетки, обычно двухмерной, как это показано на рис.4 e,f). Такие сети принято называть картами с самоорганизацией. Кроме плоской 4-угольной решетки часто используется 6-угольная (гексагональная решетка с окрестностью Галея). Но даже для одной решетки понятие соседства можно определить по-разному. Например, для 4-угольной сетки используется: 4- связность (соседними считаются 4 элемента - окрестность Фон Неймана); 8-связность (соседями являются 8 элементов с учетом “диагональных” – окрестность Мура). Карты более высокой размерности также известны, но на практике используются редко. Число входов каждого нейрона определяется размерностью входных образов (числом признаков). Каждый нейрон в слое соответствует одному классу (кластеру), поэтому количество нейронов определяет число распознаваемых различных кластеров. На рис.9 представлена сеть Кохонена. Здесь снизу вверх поступают сигналы внешних входов. На каждый нейрон поступают сигналы всех внешних входов и выходные сигналы соседних нейронов. Как видно из рисунка каждый нейрон связан со своими ближайшими соседями по определенной схеме.

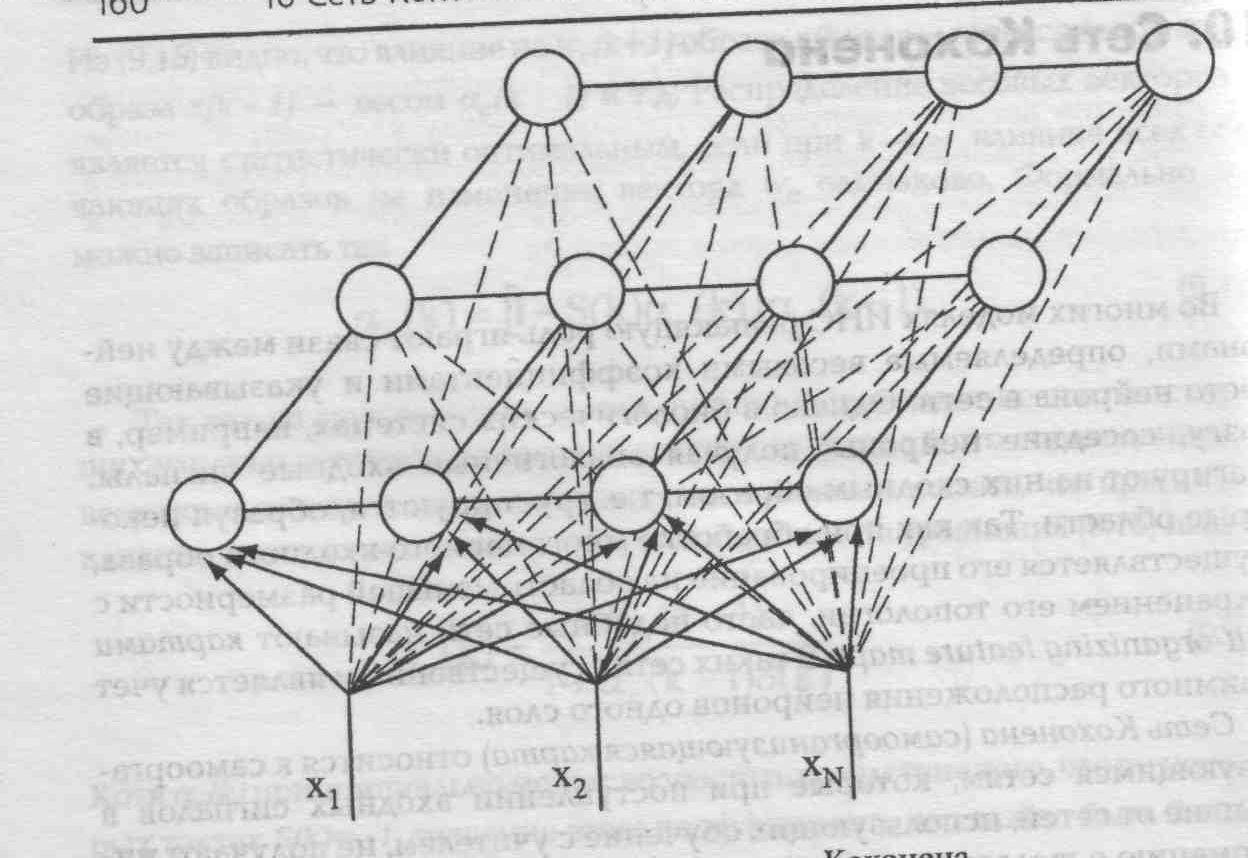
Рис.9 Архитектура самоорганизующейся сети Кохонена.

Данный тип нейронных сетей основан на конкуррентном обучении (competitivelearning), где нейроны выходного слоя соревнуются за право активации. При этом активным становится обычно один нейрон - победитель в сети или группенейронов. Таким образом, здесь реализуется принцип “победитель получает все”.

Нейроны в процессе конкуренции избирательно настраиваются на различные входные образы или классы образов. Положение таким образом настроенных нейронов упорядочивается по отношению друг к другу таким образом, что похожие входные образы отображаются в нейроны, которые близко расположены на решетке. Таким образом, координаты нейронов решетки являются индикатором статистических свойств, присущих данным входным образам. Пространственное положение выходных нейронов в топографической карте соответствуют определенной области признаков данных, выделенных из входного пространства.

Самоорганизующиеся карты разработаны по подобию человеческого мозга, который организован таким образом, что отдельные сенсорные входы представляются топологически упорядоченными картами в определенных его областях (на коре полушарий).

Как уже отмечалось, в самоорганизующихся сетях используется “обучение без учителя”. Главная черта, делающая обучение без учителя привлекательным – это его самостоятельность. Процесс обучения, как и в случае обучения с учителем заключается в подстройке синаптических коэффициентов сети. Существует несколько алгоритмов обучения.

0. Обучение по Хеббу.

Очевидно, что подстройка синапсов может проводиться только на основании информации доступной в нейроне, т.е. его состоянии (значении выходного сигнала) y_j и текущего значения синаптического коэффициента .

Исходя из этих соображений и по аналогии с известными принципами самоорганизации нервных клеток разработан алгоритм обучения Хебба, который основан на следующем правиле коррекции весов:

, (8)

где

- выходное значение i-го нейрона (n-1)-го слоя;

- выходное значение j-го нейрона n-го слоя;

- весовые коэффициенты синапса, соединяющего i-й и j-й нейроны на итерациях t и t-1 соответственно.

Очевидно, что при обучении данным методом усиливаются связи между соседними нейронами. Существует также дифференциальный метод обучения Хебба, в котором коррекция весов производится по формуле

. (9)

Из этой формулы видно, что сильнее всего обучаются синапы, соединяющие те нейроны, выходы которых наиболее динамично изменяются.

Полный алгоритм обучения выглядит следующим образом:

1. на стадии инициализации всем весовым коэффициентам присваиваются небольшие случайные значения;

2. на входы сети подается входной образ и сигнал возбуждения распространяется по всем слоям сети;

3. на основании полученных выходных значений , по формулам (8) или (9) производится изменение весовых коэффициентов;

4. переход на шаг 2, пока выходы сети не стабилизируются с заданной точностью. При этом на втором шаге цикла попеременно предъявляются все образы обучающего множества.

Вид отклика на каждый класс входных образов неизвестен заранее и представляет собой произвольное сочетание состояний нейронов обусловленное случайным распределением весов на стадии инициализации. Несмотря на это сеть обобщает похожие образы, относя их к одному классу.

1.4.2 Обучение по Кохонену

Этот алгоритм предусматривает подстройку синаптических коэффициентов на основании их значений на предыдущей итерации

. (10)

Видно, что здесь обучение сводится к минимизации разности между входными синапсами нейронов, поступающих с выходов нейронов предыдущего слоя, и весовыми коэффициентами его синапсов.

Полный алгоритм обучения имеет приблизительно такую же структуру, как и алгоритм Хебба, но на шаге 3 из всего слоя выбирается 1 нейрон, значение синапсов которого максимально подходят на входной образ X и подстройка весов этого нейрона выполняется по формуле (10). Таким образом, здесь реализуется принцип «победитель получает все». Именно этот подход называют конкурирующим (competitive) обучением. Приведенная процедура разбивает множество входных образов на кластеры, присущие входным данным. Здесь важнейшей проблемой является определение нейрона-победителя.

0. Определение нейронов-победителей в сети Кохонена.

Рассмотрим пример сети простейшей структуры с входным вектором , выходным вектором и матрицей синаптических весов . Когда входной образ подается на входы сети, активизируется только один выходной нейрон-победитель с вектором весовых коэффициентов . В правильно обученной сети входные образы из одного кластера активизируют один и тот же выходной нейрон-победитель, соответствующий этому кластеру.

Обычно применяются два метода определения нейрона победителя.

1. Первый подход основан на определении скалярного произведения

, (11)

где - входной вектор, - транспонированный j-й столбец матрицы весовых коэффициентов, соответствующий вектору синаптических коэффициентов j-очго нейрона. Для каждого j-го выходного нейрона вычисляется скалярное произведение (11) и определяется k-й нейрон с максимальным значением (11), который считается нейроном-победителем. При этом обычно вектора и нормализуются (то есть делятся на свою длину и приводятся к единичным векторам). Доказано, что если хотя бы один из векторов или подвергается нормализации, то процесс самоорганизации приводит к связному разделению пространства данных. Далее устанавливаются выходные значения нейронов для нейрона-победителя и для остальных (проигравших) нейронов.

Как только определяется победитель, его веса корректируются следующим образом:

, (12)

где деление на норму сохраняет вектор нормализованным.

Согласно этому выражению вектор весов “подкручивается” в сторону вектора , что показано на рис.10.

В процессе обучения, каждый раз, когда предъявляется текущий вектор , определяется ближайший к нему весовой вектор нейрона победителя, который “подкручивается” по направлению к . В результате вектора весов нейронов вращаются по направлению к тем областям, где находится много входных образов (т.е. кластеров), что показано на рис. 11.

Рис. 10 Вращение весового вектора в процессе обучения (W_н – вектор новых весовых коэффициентов, W_с – вектор старых весовых коэффициентов)

Рис.11 Установление весовых векторов нейронов в центры кластеров

Второй метод определения нейрона-победителя основан на вычислении евклидова расстояния. При этом в качестве победителя выбирается k-й нейрон для которого евклидово расстояние удовлетворяет условию:

(13)

Очевидно, что если вектора и нормализованы, то этот метод дает те же результаты, что и первый. После определения победителя его веса корректируются по той же формуле