1.3 Сети прямого распространения
Сети этого типа наиболее часто используются в практических приложениях и характеризуются тем, что в них сигналы распространяются в прямом направлении – от входов к выходам.
1.3.1 Однослойные сети
Исторически первыми были разработаны однослойные сети типа персептрон и методы их обучения. Персептрон представляет собой однослойную сеть, представленную на рис.4 а) и состоящую из нейронов, имеющих пороговые активационные функции. Данный класс НС предназначен для классификации линейно разделимых классов, в которых образы различных классов можно разделить некоторой гиперплоскостью. Персептрон, состоящий из одного нейрона, может решать задачу разделения только двух классов. Увеличивая число нейронов, можно решать задачу классификации на большее число классов.
Рассмотрим более детально один двухвходовой персептрон, показанный на рис.5.
Рис.5 Персептрон с 2 входами
Здесь
EMBED
Equation.3
и
.
Отметим, что функцию S можно использовать в качестве решающей или дискриминантной функции для распознавания образов.
Пусть распознаваемый
образ представлен
.
Будем считать, что
если
,
то образ принадлежит первому классу (
- точка выше
разделяющей прямой на рис.6) ;
если
,
то образ принадлежит второму классу (
- точка ниже разделяющей прямой);
при
решение принимается случайно (точка
находится на прямой).
Рис. 6 Два линейно-разделимых класса
Рассмотрим обратную
задачу: есть обучающая выборка, то есть
множество образов с известной для
каждого образа принадлежностью к классу.
Требуется найти синаптические коэффициенты
таким образом, чтобы образы первого
класса отделялись от второго. В
графической интерпретации необходимо
найти линию (или гиперплоскость),
разделяющую образы двух классов. Для
этого можно использовать, например,
классический алгоритм обучения
персептрона, который представлен
ниже.
В основе данного алгоритма лежит принцип поощрения и наказания.
1. Всем весам сети присваиваются некоторые малые случайные значения (чтобы сеть сразу не могла войти в состояние насыщения).
2.
На вход сети подается очередной входной
вектор 
и
вычисляется 
.
3.Подстройка весовых коэффициентов производится по следующим правилам.
если
и
,
то
если
и
,
то
иначе
4. Повторение пунктов 2,3 пока результаты текущей итерации не совпадут с результатами предыдущей итерации.
Доказана сходимость
данного алгоритма для линейно разделимых
классов. В случае линейно неразделимых
классов этот алгоритм “циклит”. Алгоритм
использует “обучение с учителем”, где
учитель подает на входы персептрона
входной образ и сообщает его принадлежность
определенному классу. Обучающая выборка
состоит изk входных
векторов
,
,для каждого из которых указан требуемый
выходной вектор
.
Компоненты входного вектора задаются
непрерывным диапазоном значений,
компоненты требуемого выходного вектора
являются бинарными (0,1). Подобный подход
при соответствующем кодировании образов
позволяет распознавать достаточно
сложные образы.
Для примера на рис.7 представлен персептрон, распознающий буквы русского алфавита. Он имеет 12 двоичных входов по числу клеток входного поля и 33 выхода, каждый из которых соответствует своей букве. Буква кодируется двоичным 12-разрядным вектором X=(x1,…,x12). Каждыйi-й разряд соответствует своей клетке иxi=1 в том случае, если изображение данной буквы хотя бы частично “закрашивает” эту клетку. Например, буква ‘А’ кодируется входным вектором (010010111101)
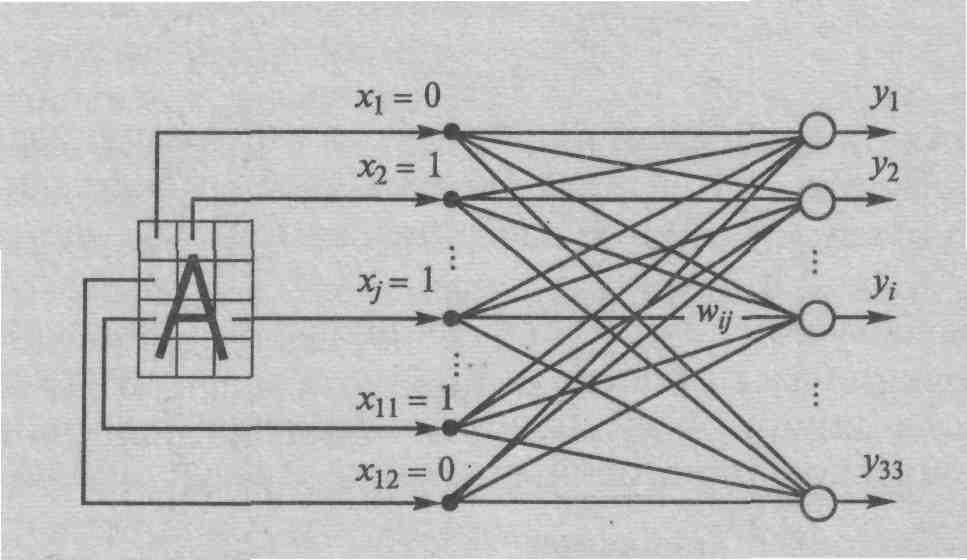Рис.7
Персептрон для распознавания букв
К сожалению однослойные НС способны работать только с линейно разделимыми классами и не могут решать другие задачи, например, проблему исключающего ИЛИ, что вызвало в свое время массу критических работ (прежде всего Минского) и замедлило развитие теории НС. Для устранения этих недостатков были предложены многослойные НС прямого распространения.