
- •О понятии множества
- •Операции над множествами, их приоритеты
- •Бесконечными множествами.
- •Счетные множества
- •Мощность континуума
- •Числовые множества
- •Аксиомы сложения
- •Аксиомы умножения
- •Аксиомы порядка
- •Аксиома полноты (непрерывности)
- •A c b.
- •Тождества алгебры множеств:
- •Замечание к тождествам 11:
- •Замечания ко всем тождествам с множествами, появляющимся при действиях с ними:
- •Отношения порядка
Числовые множества
На всех этапах развития математики представления о числе определяли уровень значимости математических знаний. Глубокое проникновение в теорию числовых множеств сочеталось с мистическим и наивным пониманием их свойств. Многие достижения теории чисел появлялись как дерзкие догадки человеческой мысли.
Представление о числе существовало еще в далекой древности, но лишь в XIX веке эти знания стали формироваться в строгую научную теорию.
Вам
поклоняюсь, вас желаю, числа!
Свободные,
бесплотные, как тени,
Вы
радугой связующей
повисли
К
раздумиям с вершины вдохновенья.
ВалерийБрюсов
Число
есть сущность всех вещей.
Пифагор
Чтобы освободить алгебру от геометрической формы, требовалось создать общее представление о числах и действиях над ними, не основанное на геометрии.
Понятие действительного числа появилось в математике не сразу. Многие задачи теории действительных чисел имеют очень
Бог
создал натуральный ряд, остальное –
дело рук человеческих.
Л.
Кронекер
Потребности счета предметов привели к появлению множества натура-льных чисел
![]() .
.
Далее практическая деятельность расширила понятие числа. Возникли целые числа
![]()
и рациональные числа
![]() ,
,
где
![]()
Будем считать, что дробь
![]()
несократима, в разложениях m и n нет общих множителей. Это позволяет добиться однозначности в записи рациональных чисел.
Введение рациональных чисел оказалось
еще недостаточным для решения некоторых
задач. Например, диагональ квадрата со
стороной, равной 1,
не может быть представлена рациональным
числом. Появились новые числа–иррациональные.
Уже Аристотель пытался доказать, что![]() –число
иррациональное.
–число
иррациональное.
Можно сказать, что рациональные числа заполняют не всю числовую прямую. Стремление поставить в соответствие каждой точке прямой некоторое число привело к появлению новых чисел – иррациональных чисел.
На рубеже XIX и XX веков Р. Дедекиндом была создана теория иррациональных чисел, согласно которой с помощью метода сечений в области рациональных чисел каждое иррациональное число может быть с любой степенью точности выражено через рациональные числа. То есть всякое иррациональное число может быть заключено в сколь угодно малый интервал, границы которого – рациональные числа.
Рассмотрим число
![]() .
Покажем, что не существует рационального
числа– ни
целого, ни дробного, квадрат которого
равен 2.
.
Покажем, что не существует рационального
числа– ни
целого, ни дробного, квадрат которого
равен 2.
Предположим противное: «найдется такое
рациональное число x,
что![]() .»
Очевидно, среди целых чисел нет числа,
равного
.»
Очевидно, среди целых чисел нет числа,
равного![]() ,
так как
,
так как![]() .
Кроме того,
.
Кроме того,![]() ,
так как
,
так как![]() .
Каждое положительное рациональное
число, не равное0,
можно представить в виде несократимой
дроби. Примем
.
Каждое положительное рациональное
число, не равное0,
можно представить в виде несократимой
дроби. Примем
![]()
где m иn– натуральные числа, не имеющие других общих делителей, кроме1. Тогда должно быть верным равенство
![]()
или
![]() .
Следовательно,m2– число четное, а значитmтоже четно (mне может быть нечетным, так как его
квадрат был бы также нечетным). Еслиm
= 2k,
то
.
Следовательно,m2– число четное, а значитmтоже четно (mне может быть нечетным, так как его
квадрат был бы также нечетным). Еслиm
= 2k,
то![]() или
или![]() ,
то естьn– число четное. Мы видим, что у несократимой
дроби и числитель, и знаменатель–
числа четные, что невозможно ввиду
несократимости дроби
,
то естьn– число четное. Мы видим, что у несократимой
дроби и числитель, и знаменатель–
числа четные, что невозможно ввиду
несократимости дроби![]() , следовательно
, следовательно![]() не есть рациональная дробь.
не есть рациональная дробь.
Совокупность рациональных и иррациональных чисел образует множество R–МНОЖЕСТВО действительных чисел. Их называют ещеВЕЩЕСТВЕННЫМИ ЧИСЛАМИ. В математике рассматриваются различные, эквивалентные, способы введения действительных чисел. Мы определим их как бесконечные десятичные дроби вида
![]() ,
,
где
![]() – некоторое
целое неотрицательное число,
– некоторое
целое неотрицательное число,![]() –
цифры0, 1,
2, ... , 9. Из двух знаков “”
берется только один: для положительных
чисел– знак
“+”, для
отрицательных чисел–
знак “–”.
Знак “+”
обычно опускают.
–
цифры0, 1,
2, ... , 9. Из двух знаков “”
берется только один: для положительных
чисел– знак
“+”, для
отрицательных чисел–
знак “–”.
Знак “+”
обычно опускают.
Рациональные числа представимы в виде бесконечных десятичных периодических дробей, иррациональные –в виде бесконечных непериодических десятичных дробей. Некоторые рациональные числа являются конечными десятичными дробями, однако они могут быть заданы и в виде бесконечных десятичных дробей с нулем в периоде или же в виде бесконечной десятичной дроби с цифрой9в периоде.
Например,
![]() ,
,
или
![]() .
.
Действительное
число
![]() равно числу
равно числу
![]() водном из
следующих случаев:
водном из
следующих случаев:
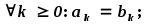 знак общности «
знак общности « »
в словесной формулировке заменяют
слова «для каждого, для любого…».
»
в словесной формулировке заменяют
слова «для каждого, для любого…».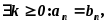
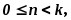
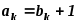 и
и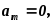
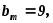 если
если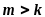 ;
(при
;
(при
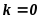 равенство с индексом
равенство с индексом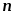 следует опустить). Знак существования
«
следует опустить). Знак существования
« »
заменяют словами «существует, найдётся
какой-нибудь, хотя бы один …».
»
заменяют словами «существует, найдётся
какой-нибудь, хотя бы один …».
В противном случае считают
![]() .
.
Сравним неравные между собой числа. Здесь возможны три случая.
1. aиb– неотрицательны.
При![]() всегда найдется натуральноеn
(илиn=0),
что
всегда найдется натуральноеn
(илиn=0),
что![]() и
и![]() .
Будем считать, чтоa
b,
еслиan
bn
, и
a
b,
еслиan
bn.
.
Будем считать, чтоa
b,
еслиan
bn
, и
a
b,
еслиan
bn.
2. a – неотрицательно число, b – отрицательно. Тогда считают a b. (При a b точка a на числовой оси лежит правее точки b).
Искусство
аналитиков состоит в том, что они,
устраняя неизящные вычисления,
разрабатывают алгебраические идеи и,
таким образом, вместо созерцания
пространства пользуются рассматриванием
чисел.
Энциклопедия
элементарной математики
(
Одесса, 1914 г. )
Запись
![]() означает, что либо
означает, что либо![]() ,
либо
,
либо![]() .
.
Множество действительных чисел Rможно изобразить точками числовой
прямой, на которой выбрано начало отсчетаO,
масштаб (единичный отрезок) и её
положительная ориентация: точкеМ,
лежащей справа от точкиО,
поставим в соответствие числоc
> 0, равное длине отрезкаОМ,
точкеР,
расположенной слева от точкиО,–число
d < 0,
где|d|–длина отрезкаОР,
а точкеО– число0.
Примем без доказательства, что между
точками прямой и множеством действительных
чисел существует взаимно однозначное
соответствие. Вот почему множество
действительных чисел называют числовой
прямой, а сами числа–
точками. Таким образом,![]() –множество
всех действительных чисел (числовая
прямая).
–множество
всех действительных чисел (числовая
прямая).
Напомним здесь уже известную терминологию:
![]() –
отрезок
(сегмент)–множество всех действительных чиселx,
удовлетворяющих неравенству
–
отрезок
(сегмент)–множество всех действительных чиселx,
удовлетворяющих неравенству![]() ;
;
![]() –
интервал–множество
всех действительных значенийx,
удовлетворяющих неравенству
–
интервал–множество
всех действительных значенийx,
удовлетворяющих неравенству![]() ;
;
![]() или
или![]() –полуинтервал
(полусегмент)–множество всех действительных чиселx,
удовлетворяющих неравенству
–полуинтервал
(полусегмент)–множество всех действительных чиселx,
удовлетворяющих неравенству![]() или
или![]() ;
ясно, что
;
ясно, что
![]() – полупрямые
– множества действительных чисел,
удовлетворяющих неравенствам:
– полупрямые
– множества действительных чисел,
удовлетворяющих неравенствам:
![]()
Для них
верно:
![]()
Отрезок, интервал, полуинтервал, полупрямую и числовую прямую будем называть промежутками.
Рассматривают в математическом анализе
также окрестность
точки c,
как любой интервал, содержащий точкус,
и–окрестность
точки
с
(
>
0)
–
интервал![]() .–окрестность
может быть задана в виде множества
.–окрестность
может быть задана в виде множества![]()
![]() .
Читают: «Множество
.
Читают: «Множество![]() состоит из таких элементовх,
что модуль разности (х
– с), для них, меньшеε».
состоит из таких элементовх,
что модуль разности (х
– с), для них, меньшеε».
Множество
![]() =
=![]() называютпроколотой
–окрестностью
точки
с. Это есть интервал
называютпроколотой
–окрестностью
точки
с. Это есть интервал![]() ,
из которого исключена точкас.
,
из которого исключена точкас.
На множестве действительных чисел вводятся основные операции –сложения и умножения, а также отношения между действительными числами– отношения порядка, обладающие следующими свойствами.
