Операции над множествами, их приоритеты

Введем операции над множествами и установим некоторую аналогию с операциями над другими математическими объектами, например, высказываниями.

Операции над множествами и их свойства во многом аналогичны алгебре высказываний в математической логике. Это отражает единство математической науки и, благодаря использованию методов математического моделирования, позволяет находить ее связь с различными областями знаний.

ОБЪЕДИНЕНИЕМ множествAиBназывается множество , содержащее те и только те элементы, которые принадлежат хотя бы одному из множествAилиB, без повторений.

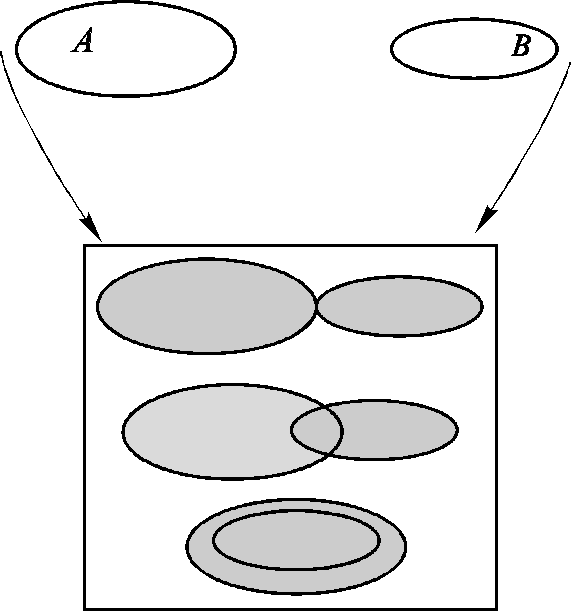
Схематично эта операция изображена на рис. 7.1. с помощью кругов Эйлера. (По приоритету уступает операциям дополнения и пересечения, определённых ниже)

Рис. 7.1. Объединение множеств .

Важно, что каждый элемент из множествAиB включаются в их объединение , без повторений, толькоодин раз, даже при их наличии одновременно и в A, и вB.

Эта операция удовлетворяет коммутативному и ассоциативному законам:

Проиллюстрируйте геометрически эти законы.

Очевидны соотношения:

Множество EназываетсяУНИВЕРСАЛЬНЫМ для некоторой системы множеств, если каждое из них принадлежит этому множеству, то есть является его подмножеством. Его ещё, часто, обозначаютU.

Можно считать поэтому, что

Важно заметить, что универсальное множество Еможет быть «индивидуальным» для каждой отдельной задачи, то есть определяться её условием. Например, при решении линейной задачиnx = m, гдеn  N– множество натуральных чисел иm  Z – множество целых чисел, тоx = m/n  Q – множество рациональных чисел. Следовательно все элементы из этой задачи принадлежат универсальному множествуЕ ≡ Q, так как в этих задачахN ZQ  E, в них других чисел нет.

ПЕРЕСЕЧЕНИЕМмножествAиBназывается множество , содержащее те и только те элементы, которые принадлежат иA,и Bодновременно. Они входят в без повторений.

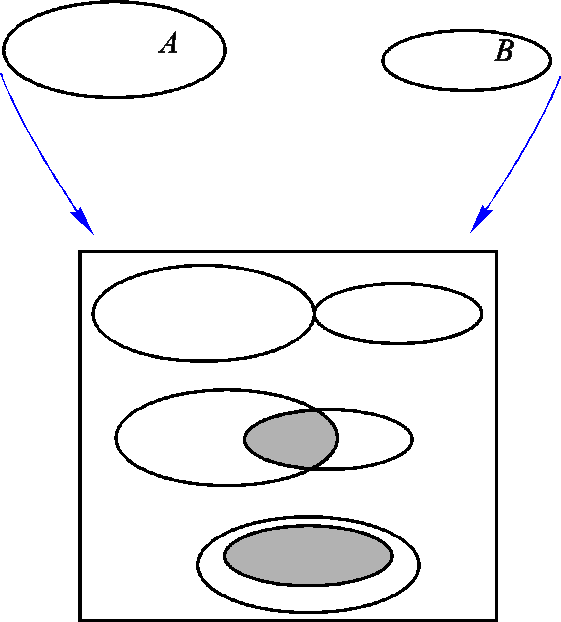
Схематично операция пересечения множеств представлена в виде кругов Эйлера на рисунке 7.2. (По приоритету эта операция занимает второе место после операции дополнения, см. ниже).

Дайте геометрическую иллюстрацию этим законам.

Для этой операции также справедливы коммутативный и ассоциативный законы:

;

Множества A и B называются НЕПЕРЕСЕКАЮЩИМИСЯ, если

Операции объединения и пересечения множеств подчиняются законам дистрибутивности (распределительным законам):

;

.

Рис. 7.2. Пересечение множеств .

РАЗНОСТЬЮ двух множествAиBназывается множествоA\B, состоящее из тех и только тех элементов, которые принадлежатA, но не принадлежатB. (Эта операция имеет самый низкий приоритет).

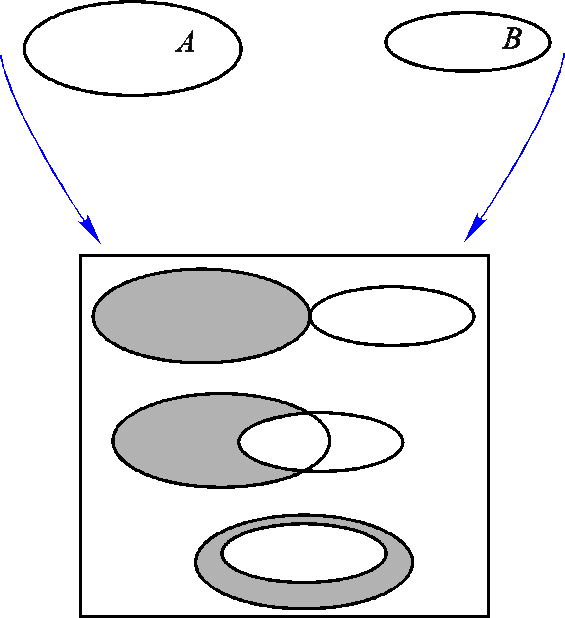
Рис. 7.3. Разность множеств .

Результаты применения этой операции изображены на рис. 7.3.

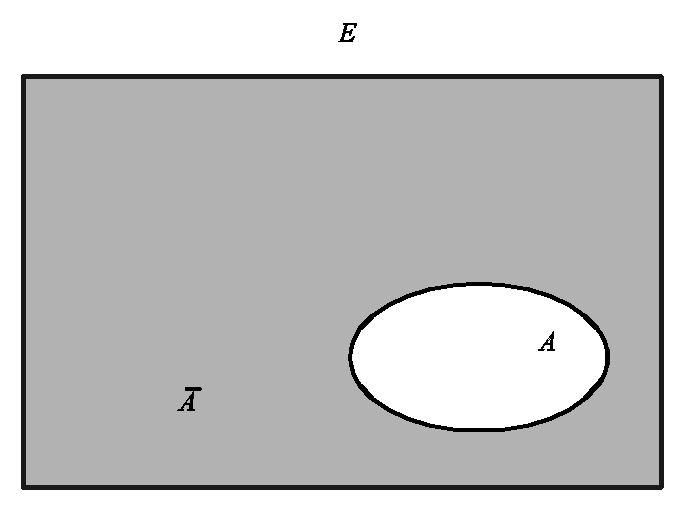
ДОПОЛНЕНИЕМмножестваAдо универсального множестваE называется разностьE\Aи обозначается (рис. 7.4). (Эта операция имеет наивысший приоритет – выполняется первой). Рисунок 7.4 является простейшей диаграммой Вена, включающей и универсальное множествоЕ, и его подмножестваA и :Е = A U .

Рис. 7.4. Дополнение множества Адо универсального множестваЕ :.

Символ «:» читают, как «такое, что …», «для … верно, что …».

Дайте им геометрическую трактовку.

Cправедливы соотношения:

Какие аналогии можно установить между операциями над множествами и, например, логическими операциями?

1. .

2. .

3. .

Интерпретируйте логи-ческими высказываниями эти соотношения.

4. .

5. .

Предложите аналоги на языке множеств для известных Вам логических тавтологий.

6. .

7. .

Приоритеты: Существует, как и в алгебре, строгий порядок выполнения действий с множествами. Первым выполняется действие в скобках. Когда скобки отсутствуют, первой выполняется операция “дополнение”, второй – “пересечение”, третьей – “объединение” и четвёртой – операция “исключение”, слева направо.

Числом часто обозначают количество элементов множества A, если оно конечно. Его называют мощностью множества A .

Для конечных множеств AиBсправедлива формула:

( 7. 1 )

Действительно, если множества AиBне пересекаются, то , его мощность , и поэтому верно . Если множестваAиBпересекаются, то количество элементов в объединении множеств, ,складывается из элементов множествAиB, без повторений. Но, так как элементы, находящиеся в пересечении множеств ,учитываются вm(A) + m(B)дважды (рис. 7.5), справедливо равенство (7.1).

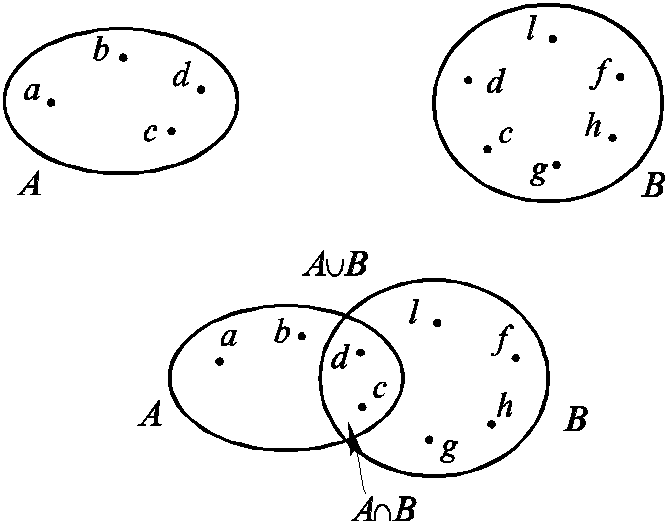
Конкретный пример с обозначением элементов дан на рис. 7.5.

Рис. 7.5. Общие элементы в объединении конечных пересекающихся множеств.

Если множества конечны, то сравнение числа их элементов может быть уподоблено сравнению натуральных чисел. Труднее сравнить множества бесконечные. Чего больше: натуральных чисел, рациональных или действительных чисел, точек отрезка или точек квадрата, построенного на нем? Очевидно, что часть меньше целого. Но будет ли это “очевидное” сохраняться, когда мы имеем дело с бесконечными множествами? Изучение феноменов «бесконечного» породило принципиально новые оценки самих множеств.

Сам Г. Кантор определил понятие мощности множества весьма расплывчато: “Мощностью данного множества Аназывается идея, которая остается у нас, когда мы мыслями об этом множестве отвлекаемся как от всех свойств его элементов, так и от их порядка”.

Г. Кантор

Соответствия между множествами

Математика не всегда интересуется природой элементов множеств, больший интерес представляет сравнение множеств. Поэтому должна быть введена универсальная характеристика, которая могла бы их описать. Этой характеристикой стала мощность множества.

МОЩНОСТЬконечного множества – это число его элементов.

Определение кажется тривиальным. Однако такой критерий для оценки бесконечных множеств будет, вряд ли, приемлем, так как простой пересчет элементов множества для их последующего сравнения невозможен.

“Я далек от мысли, что я могу сказать последнее слово в столь трудном, сложном и всеобъемлющем вопросе, как проблема бесконечности”.

Г. Кантор

Г. Кантор нашел выход из создавшегося положения. Он предложил установить связь между любыми множествами, включая и конечные множества, через взаимно однозначное соответствие. Это явилось принципиально новым взглядом на теорию множеств. Пусть, например, дан репертуар оперных спектаклей театра, составленный на неделю. Представим его в виде таблицы9.

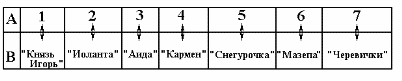
Таблица 9. Соответствие между элементами конечных множеств.

Тогда между множеством и множеством B={“Князь Игорь”, “Иоланта”, ..., “Черевички”} может быть установлено соответствие, по которому каждому элементу множества А указывается один определенный элемент множества В и обратно: каждому элементу множества В ставится в соответствие также один определенный элемент множества A. Этот способ позволяет без пересчета указать, что множества A и B содержат одинаковое количество элементов. Именно эта идея и положена в основу сравнения бесконечныхмножеств.

Будем говорить, что между множествами AиBустановленоВЗАИМНО ОДНОЗНАЧНОЕ СООТВЕТСТВИЕ, если каждому элементу множестваАпоставлен в соответствие один элемент множестваB, а каждому элементу множестваB– один элемент множестваА.

Если между множествами AиBудается установить взаимно однозначное соответствие, то говорят, что ониЭКВИВАЛЕНТНЫ, или имеютОДИНАКОВУЮ МОЩНОСТЬ.

Для таких множеств принята запись :

Читают: «Множество Aэквивалентно множествуB».

Мощность конечных множеств есть численная характеристика, совпадающая с числом элементов множества. А «мощность» бесконечных множеств есть характеристика сравнительная, вытекающая из возможности установить взаимно однозначное соответствие между парами различных множеств.

Рассмотрим примеры.

1. Пусть A = N–множество натуральных чисел, аB–множество их квадратов.

Установим следующее взаимно однозначное соответствие между этими множествами (см. таблицу 10). Мы видим, что это возможно.

Таблица 10. Взаимно однозначное соответствие между