Лабораторная работа № 1 по кс оценка трудоемкости алгоритма

Цель работы:

Освоение методов анализа трудоемкости вычислительных алгоритмов.

Задача, подлежащая решению на ЭВМ, может быть охарактеризована количеством данных, сложностью алгоритма, трудоемкостью алгоритма.

Под сложностью алгоритма понимается количество информации, необходимое для его описания. Оценка сложности алгоритма может быть дана в битах, байтах, количестве символов определенного языка. Для оценки могут использоваться также число операторов конкретного алгоритмического языка, количество машинных кодов и т.д. Предварительная оценка сложности алгоритма и количества данных выполняется экспертным путем, а точные значения могут быть известны только после завершения программирования. Сложность алгоритма и количество данных характеризуют потребность задачи в оперативной и внешней памяти.

Под трудоемкостью алгоритма понимается количество вычислительной работы, требуемой для его реализации. Трудоемкость характеризует затраты времени для реализации алгоритма на некоторой совокупности технических средств. Обычно трудоемкость оценивается количеством процессорных операций и операций ввода-вывода. Следует сразу оговориться, что трудоемкость алгоритма является в общем случае случайной величиной и зависит от исходных данных. Поэтому трудоемкость алгоритма может быть определена только приближенно в терминах теории вероятности: математическими ожиданиями, дисперсией и т.д.

Трудоемкость алгоритма в первом приближении может быть охарактеризована следующим набором параметров:

- среднее количество процессорных операций, необходимых для одной реализации алгоритма;

среднее количество обращений к файлам за один прогон программы через ЭВМ;

среднее количество информации, передаваемое за одно обращение к файлам .

При необходимости набор параметров, характеризующих трудоемкость алгоритма может быть расширен.

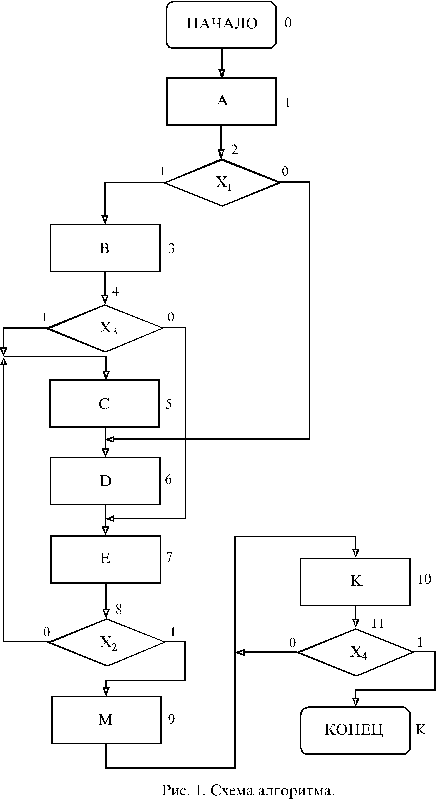
Исходная информация для расчета трудоемкости алгоритма может быть взята из схемы алгоритма, используемого обычно для разработки программы. Пример такой схемы алгоритма приведен на рис. 1. Для расчета трудоемкости алгоритма необходимо дополнительно знать вероятности переходов из логических вершин при единичном значении логического условия. Если соответствующую вероятность обозначить через p, то вероятность выхода из логической вершины при нулевом логическом значении проверяемого условия будет равна 1 - p.

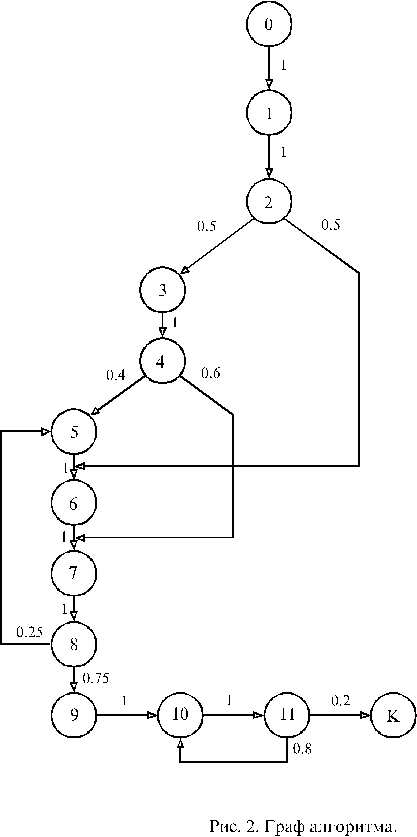
Для дальнейших расчетов схему алгоритма рациональнее изображать в виде графа алгоритма. Для этого перенумеруем все операторы схемы алгоритма. У логических операторов вместо логических условий “1” и “0” будем записывать соответствующую данному выходу вероятность. Вероятность выхода из операторной вершины равна 1. Полученный таким образом граф алгоритма изображен на рис. 2.

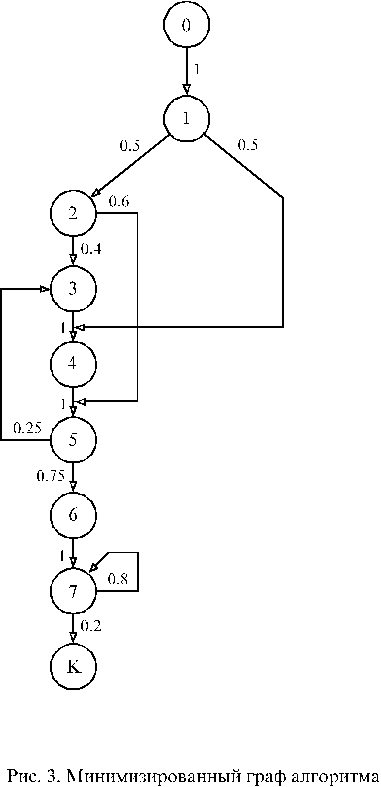
Граф алгоритма можно существенно упростить, если трудоемкость выполнения логических вершин незначительна по сравнению с трудоемкостью выполнения операторных вершин. Тогда состояния, соответствующие логическим вершинам, можно слить с предшествующими им состояниями, соответствующими операторным вершинам. В нашем примере можно слить состояния (1,2), (3,4), (7,8), (10,11). После вполне понятной перенумерации получим

минимизированный граф алгоритма, изображенный на рис. 3. При достаточном опыте к нему можно было прийти сразу от схемы алгорит-ма, приведенной на рис. 1.

Обозначим через среднее число обращений к операторам соответственно. Каждый из операторов будем характеризовать следующим набором чисел:

- среднее количество процессорных операций, выполняемых в операторе ;

- среднее количество обращений к файлу из оператора ;

- среднее количество информации, передаваемое при одном обращении к файлу из оператора .

Тогда трудоемкость алгоритма может быть оценена по следующим формулам:

; (1)

; (2)

, (3)

где - среднее число процессорных операций, выполняемых при одном прогоне алгоритма;

- среднее число обращений к файлу за один прогон алгоритма;

- среднее количество информации, передаваемое при каждом обращении к файлу , при одном прогоне программы.

Для определения среднего числа обращений n_i к оператору V_i (i=1,2,...,k-1) обычно делаются следующие допущения:

- вероятность выполнения после оператора V_i оператора V_j равна P_ij и является постоянной величиной;

- вероятность P_ij зависит только от оператора V_i, но никак не связана со способом попадания в оператор V_j, т.е. не зависит от предыстории вычислительного процесса;

.

При выполнении вышеуказанных допущений вычислительный процесс является марковским процессом с состояниями S₁,S₂,...,S_k. При этом операторы V₁,V₂,...,V_k-1 соответствуют состояниям S₁,S₂,...,S_k-1. Состояние S_k соответствует конечной вершине графа алгоритма и является поглощающим, т.е. при достижении состояния процесс прекращается. Состояния S₁,S₂,...,S_k-1 называются невозвратными, так как процесс непременно их покидает.

В настоящее время существует несколько способов оценки трудоемкости алгоритма. Рассмотрим некоторые из них.

Оценка трудоемкости алгоритмов методами

теории марковских цепей

Для определения среднего числа процессорных операций, выполняемых за один прогон программы, следует граф алгоритма записать в виде стохастической матрицы P. Для рис.3 она примет вид:

	S1	S2	S3	S4	S5	S6	S7	Sk
S0	1	0	0	0	0	0	0	0
S1	0	0.5	0	0.5	0	0	0	0
S2	0	0	0.4	0	0.6	0	0	0
S3	0	0	0	1	0	0	0	0
S4	0	0	0	0	1	0	0	0
S5	0	0	0.25	0	0	0.75	0	0
S6	0	0	0	0	0	0	1	0
S7	0	0	0	0	0	0	0.8	0.2

Элементами матрицы P являются вероятности перехода из состояния i в состояние j, которые приведены на графе алгоритма.

Из стохастической матрицы следует, например, что в состоянии S₄ процесс может оказаться при переходе из S₁ с вероятностью 0.5 или при переходе из состояния S₃ с вероятностью 1. Если известны средние числа обращений к вершинам V₁ и V₃ , то число обращений к вершине V₄ будет соответственно равно:

n₄ = p₁₄ n₁ + p₃₄ n₃ = 0.9n₁ + n₃ .

В самом общем случае можно записать ( суммирование по столбцу стохастической матрицы ):

, (n₀ = 1, i = 1,2,...,k-1). (4)

Последняя запись представляет собой систему линейных алгебраических уравнений, решение которых даст искомое среднее число обращений к операторам.

Для примера из стохастической матрицы имеем:

n₁ = 1n₀ = 1*1 = 1 ;

n₂ = 0.5n₁ = 0.5*1 = 0.5 ;

n₃ = 0.4n₂ + 0.25n₅ = 0.2 + 0.25n₅ ;

n₄ = 0.5n₁ + n₃ = 0.5 + n₃ ;

n₅ = 0.6n₂ + n₄ = 0.3 + n₄ ;

n₆ = 0.75n₅ ;

n₇ = n₆ + 0.8n₇ .

Решая систему уравнений, получим:

n₁ = 1; n₂ = 0.5; n₃ = 0.533; n₄ = 1.033;

n₅ = 1.333; n₆ = 1; n₇ = 5.

Для проверки правильности решения системы линейных уравнений можно использовать очевидное тождество:

, при n₀ = 1. (5)

В приведенном примере это выполняется так: n_k = 0.2 * n₇ = 0.2 * 5 = 1.

Данный метод является универсальным ( в случае марковского процесса ), но требует больших затрат времени при значительных размерах стохастической матрицы.