ЧМ_стац / Численные методы лекции / 7. Системы нелинейных уравнений

7. Решение систем нелинейных уравнений

Многие практические задачи сводятся к решению систем нелинейных уравнений. Пусть для вычисления неизвестных х₁, х₂,…,х_n требуется решить систему из n нелинейных уравнений

… (7.1)

В отличие от систем линейных уравнений не существует прямых методов решения систем нелинейных уравнений общего вида. Лишь в отдельных случаях систему можно решить непосредственно. Например, для случая двух уравнений иногда удается выразить одно неизвестное через другое и таким образом свести задачу к решению одного нелинейного уравнения относительно одного неизвестного.

Для решения систем нелинейных уравнений обычно используются итерационные методы.

7.1. Метод простых итераций

Систему уравнений представим в виде

… (7.2)

Алгоритм решения этой системы методом простых итераций напоминает метод простых итераций, используемый для решения систем линейных уравнений.

Приближение с номером k можно представить в виде

… (7.3)

Итерационный процесс продолжается до тех пор, пока изменения всех неизвестных в двух последовательных итерациях не станут малыми, то есть до достижения заданной точности

Условие сходимости выглядит для нелинейных систем следующем образом

1. Составляется матрица

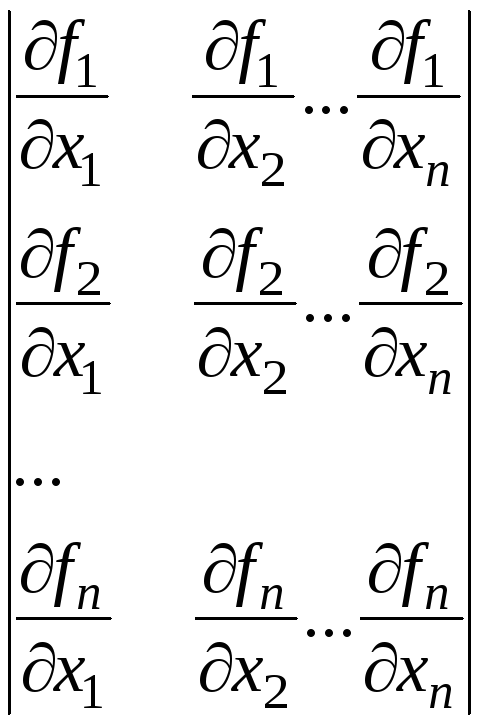
2. В выражения частных производных при вычислении значений коэффициентов матрицы используем начальное приближение

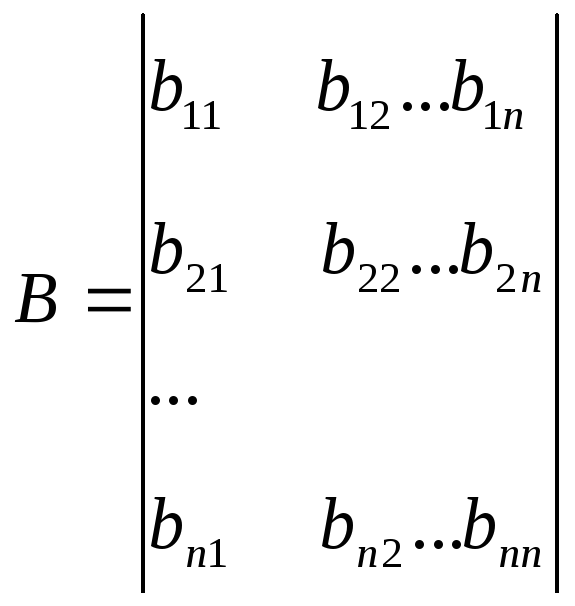
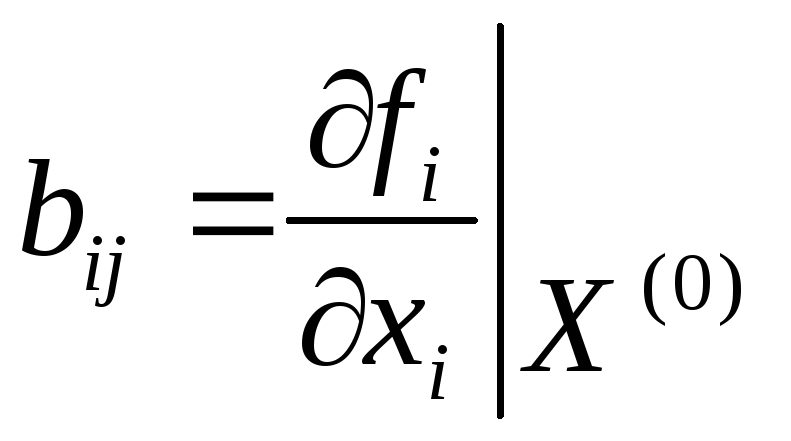
3. Определяем первую или вторую норму матрицы В соответственно

4. Условие сходимости

или

Определение начального приближения достаточно ответственный этап, так как от выбора начального приближения зависит условие сходимости итерационного процесса.

Для случая двух уравнений с двумя неизвестными начальное приближение находят графически.

7.2. Метод Зейделя

Имеет более быструю сходимость

… (7.4)

7.3. Метод Ньютона

Этот метод обладает гораздо более быстрой сходимостью, чем метод простой итерации. В основе метода Ньютона для системы нелинейных уравнений лежит использование разложения функций , в ряд Тейлора, причем слагаемые, содержащие вторые и более высокие порядки производных, отбрасываются

1. Формируем матрицу Якоби

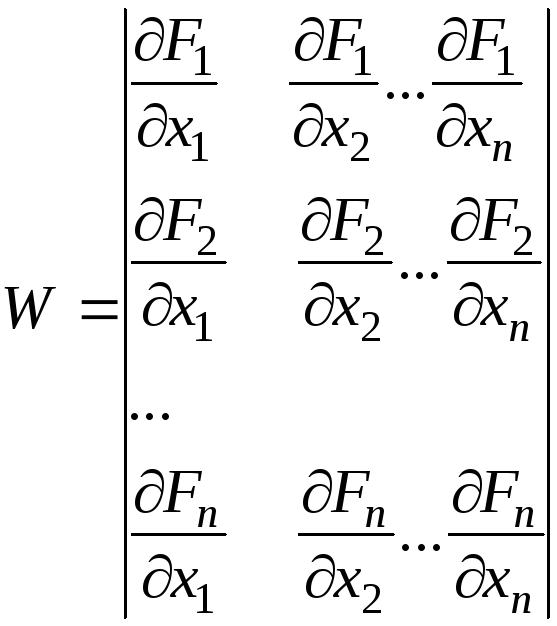
2. Составляем и решаем систему из n-линейных уравнений относительно неизвестных приращений , k – номер итерации

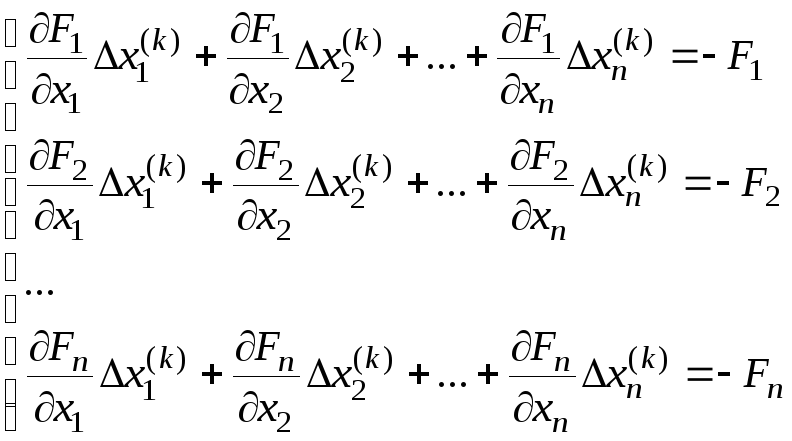(7.5)

3. Полученные значения используем для уточнения

4. Проверяем условие окончания

Если систему линейных уравнений решать методом обратной матрицы, то решение системы нелинейных уравнений в векторно – матричном представлении может быть записано следующим образом, что собственно и называется методом Ньютона

(7.6)

- обратная матрица Якоби

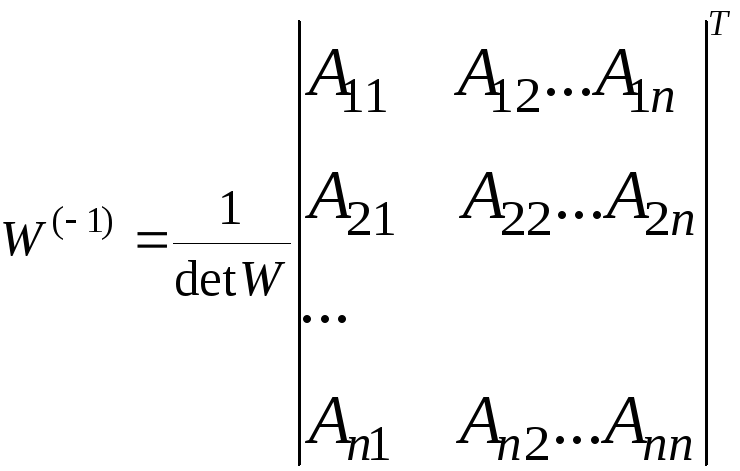
- алгебраические дополнения элементов

7.4. Модифицированный метод Ньютона

(7.7)