ЧМ_стац / Численные методы лекции / 3, Аппроксимация производных

3. Аппроксимация производных

Производная функции это предел отношения приращения функции к приращению аргумента при стремлении к 0

(3.1)

Обычно для вычисления производных используют готовые формулы (таблица производных). Однако в численных расчетах на ЭВМ использование таблицы производных не всегда удобно и возможно. В частности, если функция задана таблично. В таких случаях производную находят, опираясь на формулу (3.1). Значение полагают равным некоторому конечному числу и для вычисления производной получают приближенное равенство

(3.2)

Соотношение (3.2) называется аппроксимацией производной с помощью отношения конечных разностей, так как значения и в формуле (3.2) конечные в отличие от их бесконечно малых значений в формуле (3.1).

Рассмотрим аппроксимацию производной для функции , заданной в табличном виде: при соответственно.

Запишем выражение для производной при . В зависимости от способа вычисления конечных разностей получаем разные формулы для вычисления производной в одной и той же точке:

- с помощью левых разностей _

(3.3)

- с помощью правых разностей

(3.4)

- с помощью центральных разностей

(3.5)

Можно найти тоже выражение для старших производных

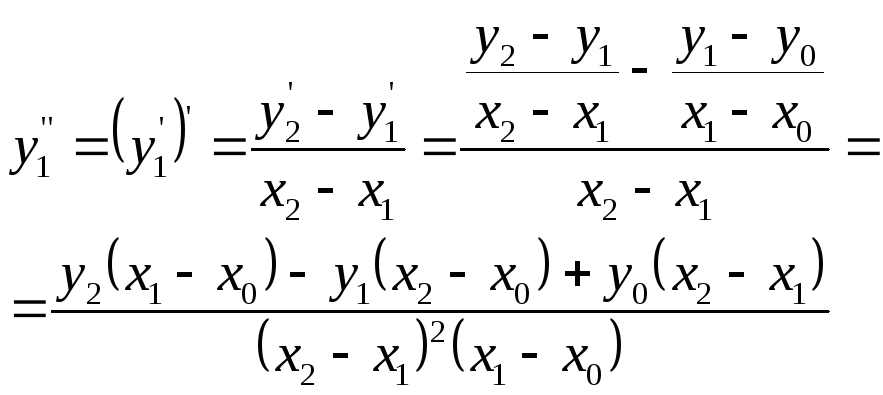(3.6).

Если , то формулы (3.3) – (3.6) примут следующий вид соответственно

,

, (3.7)

,

.

Таким образом, по формуле (3.2) можно найти приближенные значения производных любого порядка.

Правда при этом остается открытым вопрос о точности полученных значений.

Доказано, что для хорошей аппроксимации производной нужно использовать значение функции во многих узлах, а в формуле (3.2) это не предусмотрено.

В этом случае для аппроксимации производной можно использовать интерполяционные формулы.

Во избежание громоздких выражений рассмотрим аппроксимацию производных по формулам Лагранжа и Ньютона для функции, заданной таблично с равноотстоящими значениями аргумента

Запишем интерполяционный многочлен Лагранжа для случая трех узлов интерполяции и найдем их производные

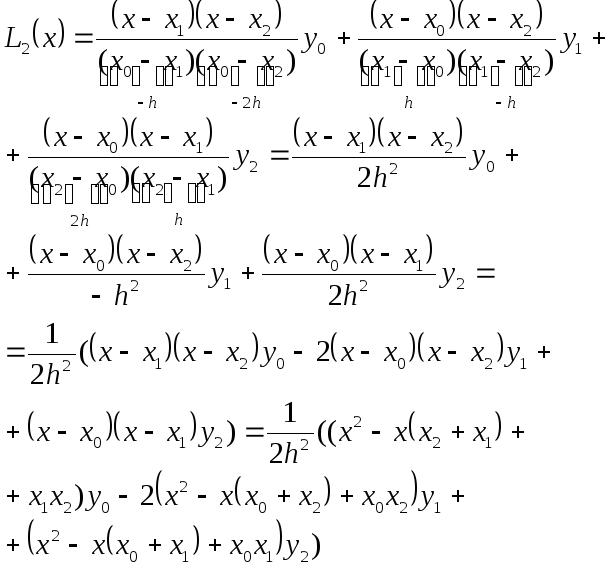
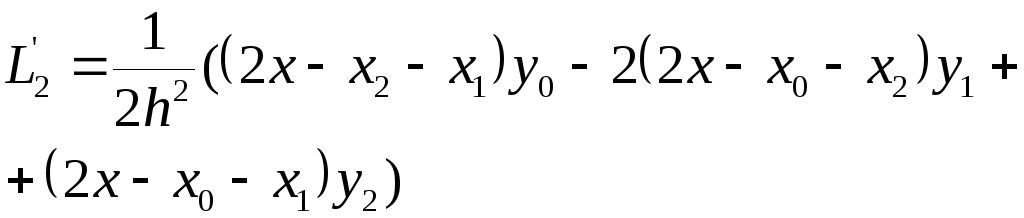
Подставив в формулу для значения можно получить выражения для вычисления

Таким образом, используя значения функции в узлах, получаем аппроксимацию производных первого порядка.

Аналогично, подставляя в значения можно получить аппроксимации для второй производной.

Запишем теперь первую интерполяционную формулу Ньютона

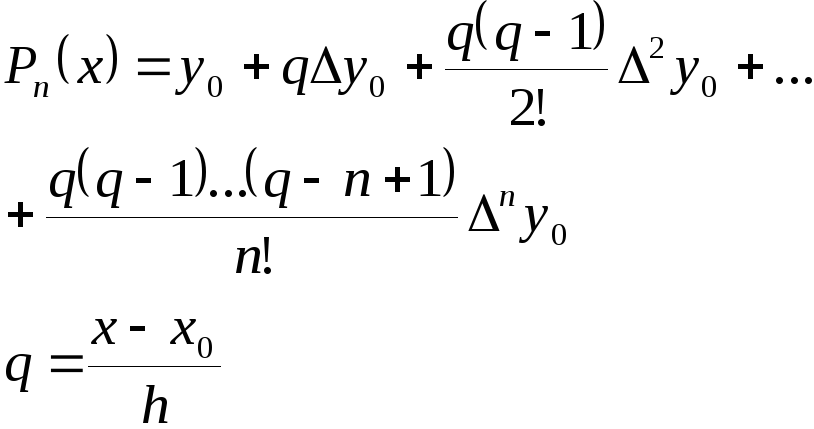
Найдем , учитывая

Подставив в полученные формулы вместо значения , получим аппроксимацию производной первого, второго порядков в узле интерполирования.