
Metodichka_TG
.pdf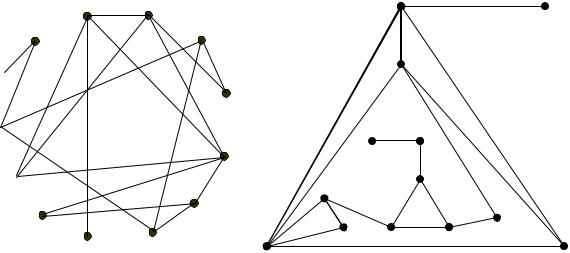
90
Построим графическое изображение графа G2.
G2: |
или: |
2 |
1
13
12 
11 
10
9
3 |
2 |
6 |
9 |
|
|
|
|
4 |
21 |
|
|
|
3 |
|
|
|
5 |
|
|
|
|
7 |
14 |
|
28 |
7 |
|
|
|
|
|||
|
|
|
|
13 18 |
1 |
|
|
6 |
|
|
|
14 |
|
|
|
|
|
|
12 |
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
7 |
18 |
7 |
21 |
6 |
12 |
|
|
12 |
|
30 |
|
6 |
5 |
8 |
|
10 |
8 |
4 |
7 |
|
|
|
|||||
|
|
|
|
|
|
|
|
6 |
|
|
|
14 |
11 |
2. Для графа G1 составить матрицу Кирхгофа и посчитать количество помеченных остовов.
Матрица Кирхгофа
M |
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
|||
1 |
2 |
|
-1 |
|
0 |
|
-1 |
|
0 |
|
|||
2 |
-1 |
|
|
3 |
|
0 |
|
-1 |
|
-1 |
|
||
3 |
0 |
|
0 |
|
1 |
|
0 |
|
-1 |
|
|||
4 |
-1 |
|
-1 |
|
0 |
|
|
2 |
|
0 |
|
||
5 |
0 |
|
-1 |
|
-1 |
|
0 |
|
|
2 |
|
||
Количество помеченных остовов k графа нию любого элемента матрицы Кирхгофа.
|
|
1 |
1 |
|
|
|
0 |
3 |
1 5 |
|
|||||
|
|
3 0 |
|
|
|
||||||||||
k |
0 |
1 |
0 |
1 |
|
|
|
0 |
1 |
0 |
1 |
( 1) |
|||
|
|
1 |
0 |
2 |
0 |
|
|
|
0 |
1 |
2 |
2 |
|
||
|
|
1 |
1 |
0 |
2 |
|
|
|
1 |
1 0 |
2 |
|
|||
|
1 |
5 |
|
|
|
|
|
|
2 1 |
|
|
|
|||
|
2 |
|
|
|
|
|
|
|
|
|
|||||
|
0 |
0 |
1 |
( 1) ( 1) |
|
4 1 3. |
|||||||||
|
1 |
2 |
2 |
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G равно алгебраическому дополне-
|
3 |
1 |
5 |
|
|
|
|||
( 1) |
1 |
0 |
1 |
|
|
1 |
2 |
2 |
|
|
|
|
|
|
91
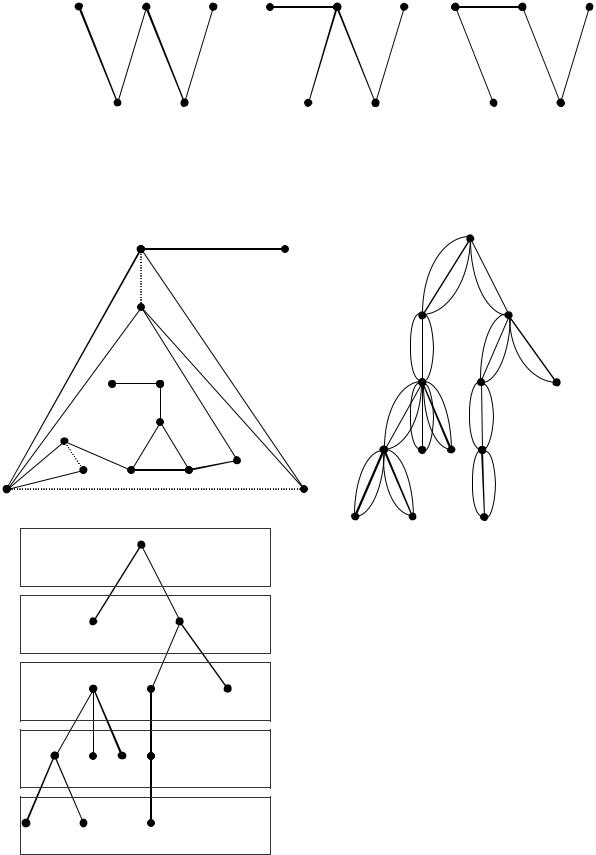
Итак, в графе G1 содержится 3 помеченных остова:
1 |
2 |
3 |
1 |
2 |
3 |
1 |
2 |
3 |
4 |
5 |
4 |
5 |
4 |
5 |
3. Для графа G2 построить дерево обхода вершин графа в ширину и в глубину.
Построим остов графа G2.
Обход в глубину:
1) |
2 |
|
3 |
|
13 |
1 |
|
|
|
|
|
12 |
7 |
|
|
|
|
5 |
10 |
8 |
4 |
6 |
|
|
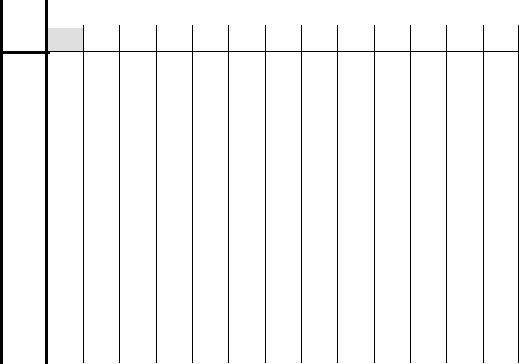
Обход в ширину: |
|
|
|
1 |
8 |
|
|
7 |
|
|
2 |
|
3 |
4 |
|
|
|
|
|
|
|||||
|
|
6 |
|
|
4 |
5 |
12 |
6 |
5 |
|
|
|
|||||||
2 |
7 |
8 |
3 9 |
1010 1 |
|
|
|||
11 |
12 |
|
11 |
13 |
13 |
|
|
||
9 |
|
|
|
||||||
9 |
|
|
|
8 |
|
|
|
1 |
|
|
|
|
|
14 |
|
15 |
|
|
|
7 |
|
|
4 |
|
2 |
13 |
16 |
|
|
|
|
21 |
22 |
||
|
|
|
|
||
|
|
6 |
|
12 |
5 |
|
3 |
11 12 |
17 |
20 |
|
|
|
|
|||
|
8 |
9 10 |
|
1 |
|
|
2 |
3 |
10 |
|
|
|
|
|
|||
4 |
6 |
7 |
18 |
19 |
|
|
|
||||
11 |
5 |
|
|
|
|
|
9 |
11 |
|
13 |
|
-1 ярус
-2 ярус
-3 ярус
-4 ярус
-5 ярус
92
Для графа G2 решить задачу построения остовов кратчайших маршрутов, используя алгоритмы Прима и Краскала (в качестве весов ребер использовать элементы матрицы Y).
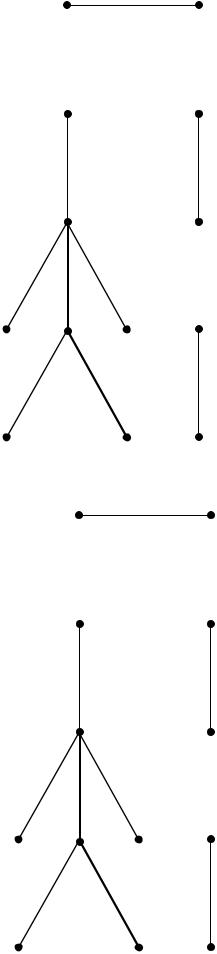
1) Алгоритм Краскала
Ребра графа G упорядочиваются в порядке не убывания их весов. На каждом шаге к пустому графу Op добавляется ребро с минимальным весом из списка ребер. Добавляемое ребро не должно приводить к образованию цикла. Алгоритм заканчивает работу, если количество ребер в графе станет равным p-1.
Матрица весов
С2 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
1 |
0 |
|
|
|
|
|
|
|
|
|
|
14 18 |
2 |
|
|
|
|
0 |
|
|
21 |
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
6 |
|
|
|
7 |
|
|
|
|
|
|
|||||||
3 |
|
|
21 |
|
|
0 |
|
|
|
12 14 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
28 |
|
|
|
|
|
|
|||||||||||
4 |
|
|
|
|
|
0 |
|
7 |
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
12 |
|
|
|
||||||||||||
5 |
|
|
|
12 7 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
6 |
|
|
7 |
|
|
14 |
|
|
|
|
|
|
|
|
|
0 |
|
18 |
|
|
|
|
|
|
|
12 14 |
|
|
|
|
|
|
||||||||||
7 |
|
|
|
|
|
|
|
|
|
18 |
|
0 |
|
21 |
|
|
|
30 |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
8 |
|
|
|
|
6 |
|
|
|
|
|
|
|
21 |
|
0 |
|
|
|
|
|
|
|
|
|
6 |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
9 |
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
10 |
|
|
|
|
|
|
|
|
|
12 |
30 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
||||||||||||
11 |
|
|
7 |
|
|
28 |
|
|
|
|
|
|
|
14 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
12 14 |
|
|
12 |
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
0 |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
13 18 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
Ребра |
|
|
|
|
|
|
Вес |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
(2,9)1, (4,8)2, (8,12)3 |
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
(2,6)4, (2,11)5, (4,5)6 |
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
(3,5)7, (4,12), (6,10)8 |
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
(1,12)9, (3,6)10, (6,11) |
14 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
(1,13)11, (6,7)12 |
|
|
|
|
|
18 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
(2,3), (7,8) |
|
|
|
|
|
|
|
|
21 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
(3,11) |
|
|
|
|
|
|
|
|
|
|
|
28 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
(7,10) |
|
|
|
|
|
|
|
|
|
|
|
30 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
93
Хорды:
|
|
|
5 |
|
6 |
|
|
|
4 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
(4,12); |
|
|
|
|
|
|
|
|
|
(6,11); |
|
|
7 |
|
|
2 |
|
|
|
(2,3); |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(7,8); |
|
|
|
|
|
|
|
|
|
(3,11); |
|
|
3 |
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
(7,10). |
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
3 |
|
|
|
|
|
12 |
6 |
|
|
9 |
|
12 |
|
|
|
|
|
|
|||||
|
|
4 |
8 |
|
|
|
|
||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||
|
7 |
|
2 |
10 |
|
|
|
1 |
|
|
|
|
|
||||||
|
|
1 |
|
5 |
|
11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2) Алгоритм Прима |
9 |
|
|
11 |
|
13 |
|||
|
|
|
|
|
|
|
|
|
|
Алгоритм Прима отличается от алгоритма Краскала тем, что на каждом шаге строится не просто ацикличный граф, а дерево.
|
|
|
|
5 |
|
7 |
|
|
|
4 |
Ребра |
Вес |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||
(2,9)1, (4,8)8, (8,12)9 |
6 |
|
|
6 |
|
|
|
|
|
|
(2,6)2, (2,11)3, (4,5)7 |
7 |
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
(3,5)6, (4,12), (6,10)4 |
12 |
|
|
|
|
|
|
|
|
|
(1,12)10, (3,6)5, (6,11) |
14 |
|
|
3 |
|
|
|
|
|
8 |
|
|
|
|
|
|
|
||||
(1,13)11, (6,7)12 |
18 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||
(2,3), (7,8) |
21 |
|
|
5 |
|
|
9 |
|
|
|
(3,11) |
28 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||
(7,10) |
30 |
|
|
|
|
|
|
|
|
|
Хорды: |
|
|
|
6 |
|
|
|
|
12 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
2 |
4 |
|
10 |
|
|
|
(4,12); |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
(6,11); |
|
|
|
|
|
|
|
|
|
|
(2,3); |
7 |
|
2 |
10 |
|
|
|
1 |
||
|
|
|
||||||||
(7,8); |
|
|
|
|
|
|
|
|
|
|
(3,11); |
|
|
1 |
|
3 |
|
11 |
|
|
|
(7,10). |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
11 |
|
13 |
||||
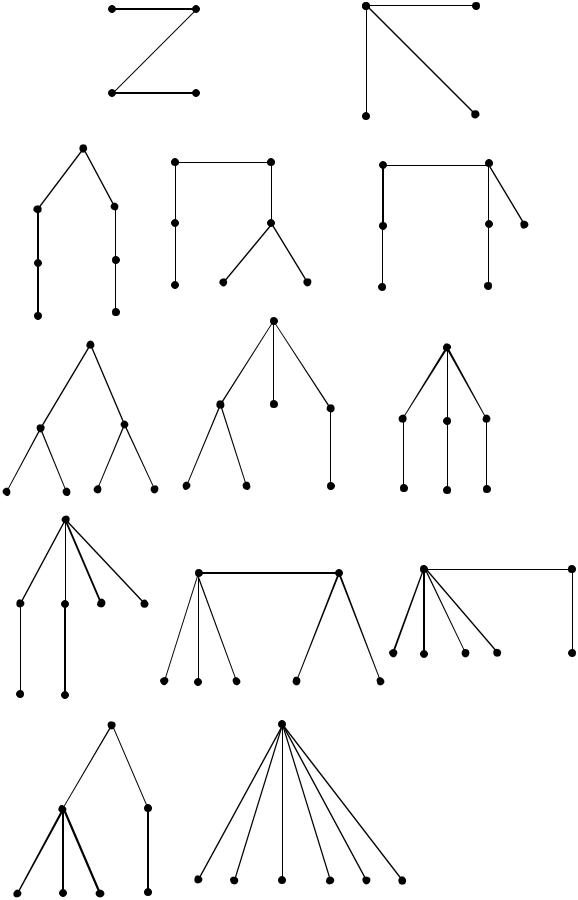
94
4. Сгенерировать все различные абстрактные не изоморфные друг другу деревья порядка 4 и 7.
Не изоморфные деревья 4-го порядка:
Не изоморфные деревья 7-го порядка:
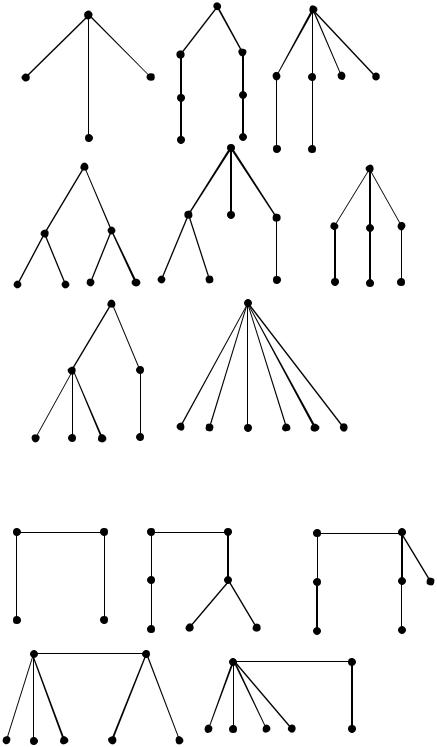
95
Разделить множество деревьев на 2 подмножества: с одной и с двумя центральными вершинами.
1) Деревья с одной центральной вершиной:
2) Деревья с двумя центральными вершинами:
Вывод: изучены понятия деревьев и остовов, приобретены практические навыки построения матрицы Кирхгофа и вычисления количества помеченных остовов.
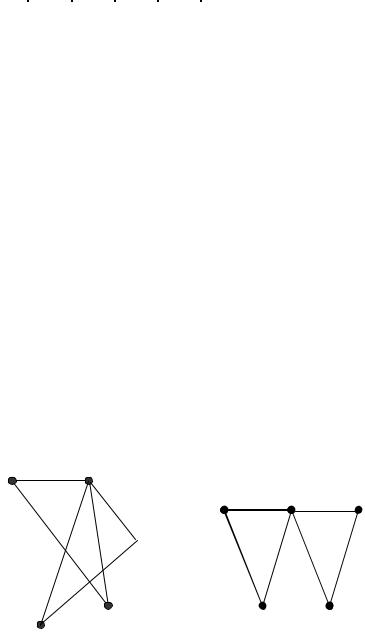
96
Тема 2: «Циклы и обходы».
Цель работы: изучение понятий гамильтоновых и эйлеровых циклов, приобретение практических навыков построения матрицы циклов и матрицы фундаментальных циклов.
1. Используя алгоритм генерации варианта GV, построить неориентирован-
ный граф G1: GV(5,{2,3}) и граф G2: GV(13,{6,7}).
Построим граф G1, используя алгоритм генерации варианта GV(5,{2,3}). S=<юфаеленаяковлевна>;
S=<ю,ф,а,е,л,н,я,к,о,в>;
n(Si)={32,22,1,6,13}. |
|
|
|
|
|
|
|
|
|
||||||||
Y1 |
32 |
|
22 |
|
1 |
|
6 |
|
13 |
|
|
|
|
||||
32 |
0 |
|
10 |
|
31 |
|
26 |
|
29 |
|
|
|
|
||||
22 |
10 |
|
|
0 |
|
21 |
|
16 |
|
9 |
|
|
|
|
|||
1 |
31 |
|
21 |
|
|
0 |
|
5 |
|
12 |
|
|
|
|
|||
6 |
26 |
|
16 |
|
5 |
|
|
0 |
|
7 |
|
|
|
|
|||
13 |
29 |
|
9 |
|
12 |
|
7 |
|
|
0 |
|
|
|
|
|||
Матрица смежности |
|
|
|
|
|
|
|||||||||||
A1 |
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
|
deg(vi) |
|||||
1 |
0 |
|
1 |
|
0 |
|
1 |
|
0 |
|
2 |
|
|||||
2 |
1 |
|
|
0 |
|
1 |
|
1 |
|
1 |
|
4 |
|
||||
3 |
0 |
|
1 |
|
|
0 |
|
0 |
|
1 |
|
2 |
|
||||
4 |
1 |
|
1 |
|
0 |
|
|
0 |
|
0 |
|
2 |
|
||||
5 |
0 |
|
1 |
|
1 |
|
0 |
|
|
0 |
|
|
2 |
|
|||
Построим неориентированный граф G1, используя способ перечисления.
G1=(V1,E1): V1={1,2,3,4,5} – множество вершин графа; E1={(1,2),(1,4),(2,3),(2,4),(2,5),(3,5)} – множество ребер графа.
Построим графическое изображение графа G1.
G1, или
1 |
2 |
1 |
2 |
3 |
 3
3
4 |
4 |
5 |
|
|
|
5 |
|
|
97
Построим граф G2, используя алгоритм генерации варианта GV(13,{6,7}).
S=<юфаеленаяковлевна>; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
S=<ю,ф,а,е,л,н,я,к,о,в>; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
n(Si)={32,22,1,6,13,15,33,12,16,3,29,18,14}. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
Y2 |
|
32 |
|
22 |
|
1 |
|
6 |
|
|
13 |
|
15 |
|
33 |
|
12 |
|
16 |
|
3 |
|
29 |
|
18 |
|
14 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
32 |
|
|
0 |
|
10 |
|
31 |
|
26 |
|
|
19 |
|
17 |
|
1 |
|
20 |
|
16 |
|
29 |
|
3 |
|
14 |
|
18 |
|
|
|
|
|||||
22 |
|
10 |
|
|
0 |
|
21 |
|
16 |
|
|
9 |
|
7 |
|
11 |
|
10 |
|
6 |
|
19 |
|
7 |
|
4 |
|
8 |
|
|
|
|
|||||
1 |
|
31 |
|
21 |
|
0 |
|
5 |
|
|
12 |
|
14 |
|
32 |
|
11 |
|
15 |
|
2 |
|
28 |
|
17 |
|
13 |
|
|
|
|
||||||
6 |
|
26 |
|
16 |
|
5 |
|
0 |
|
|
7 |
|
9 |
|
27 |
|
6 |
|
10 |
|
3 |
|
23 |
|
12 |
|
8 |
|
|
|
|
||||||
13 |
|
19 |
|
9 |
|
12 |
|
7 |
|
|
0 |
|
2 |
|
20 |
|
1 |
|
3 |
|
10 |
|
16 |
|
5 |
|
1 |
|
|
|
|
||||||
15 |
|
17 |
|
7 |
|
14 |
|
9 |
|
|
2 |
|
0 |
|
18 |
|
2 |
|
1 |
|
12 |
|
14 |
|
3 |
|
1 |
|
|
|
|
||||||
33 |
|
1 |
|
11 |
|
32 |
|
27 |
|
|
20 |
|
18 |
|
0 |
|
21 |
|
17 |
|
30 |
|
4 |
|
15 |
|
19 |
|
|
|
|
||||||
12 |
|
20 |
|
10 |
|
11 |
|
6 |
|
|
1 |
|
2 |
|
21 |
|
|
0 |
|
4 |
|
9 |
|
17 |
|
6 |
|
2 |
|
|
|
|
|||||
16 |
|
16 |
|
6 |
|
15 |
|
10 |
|
|
3 |
|
1 |
|
17 |
|
4 |
|
|
0 |
|
13 |
|
13 |
|
2 |
|
2 |
|
|
|
|
|||||
3 |
|
29 |
|
19 |
|
2 |
|
3 |
|
|
10 |
|
12 |
|
30 |
|
9 |
|
13 |
|
0 |
|
26 |
|
15 |
|
11 |
|
|
|
|
||||||
29 |
|
3 |
|
7 |
|
28 |
|
23 |
|
|
16 |
|
14 |
|
4 |
|
17 |
|
13 |
|
26 |
|
0 |
|
11 |
|
15 |
|
|
|
|
||||||
18 |
|
14 |
|
4 |
|
17 |
|
12 |
|
|
5 |
|
3 |
|
15 |
|
6 |
|
2 |
|
15 |
|
11 |
|
|
0 |
|
4 |
|
|
|
|
|||||
14 |
|
18 |
|
8 |
|
13 |
|
8 |
|
|
1 |
|
1 |
|
19 |
|
2 |
|
2 |
|
11 |
|
15 |
|
4 |
|
|
0 |
|
|
|
|
|||||
|
Матрица смежности |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
A2 |
|
1 |
|
2 |
|
3 |
|
4 |
|
|
5 |
|
6 |
|
7 |
|
8 |
|
9 |
|
10 |
|
11 |
|
12 |
|
13 |
|
|
deg(vi) |
|||||||
1 |
|
|
0 |
|
0 |
|
0 |
|
0 |
|
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
1 |
|
1 |
|
2 |
|
||||||
2 |
|
0 |
|
|
0 |
|
1 |
|
0 |
|
|
0 |
|
1 |
|
0 |
|
0 |
|
1 |
|
0 |
|
1 |
|
0 |
|
0 |
|
4 |
|
||||||
3 |
|
0 |
|
1 |
|
0 |
|
0 |
|
|
1 |
|
1 |
|
0 |
|
0 |
|
0 |
|
0 |
|
1 |
|
0 |
|
0 |
|
4 |
|
|||||||
4 |
|
0 |
|
0 |
|
0 |
|
0 |
|
|
1 |
|
0 |
|
0 |
|
1 |
|
0 |
|
0 |
|
0 |
|
1 |
|
0 |
|
3 |
|
|||||||
5 |
|
0 |
|
0 |
|
1 |
|
1 |
|
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
2 |
|
|||||||
6 |
|
0 |
|
1 |
|
1 |
|
0 |
|
|
0 |
|
0 |
|
1 |
|
0 |
|
0 |
|
1 |
|
1 |
|
0 |
|
0 |
|
5 |
|
|||||||
7 |
|
0 |
|
0 |
|
0 |
|
0 |
|
|
0 |
|
1 |
|
0 |
|
1 |
|
0 |
|
1 |
|
0 |
|
0 |
|
0 |
|
3 |
|
|||||||
8 |
|
0 |
|
0 |
|
0 |
|
1 |
|
|
0 |
|
0 |
|
1 |
|
|
0 |
|
0 |
|
0 |
|
0 |
|
1 |
|
0 |
|
3 |
|
||||||
9 |
|
0 |
|
1 |
|
0 |
|
0 |
|
|
0 |
|
0 |
|
0 |
|
0 |
|
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
1 |
|
||||||
10 |
|
0 |
|
0 |
|
0 |
|
0 |
|
|
0 |
|
1 |
|
1 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
2 |
|
|||||||
11 |
|
0 |
|
1 |
|
1 |
|
0 |
|
|
0 |
|
1 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
3 |
|
|||||||
12 |
|
1 |
|
0 |
|
0 |
|
1 |
|
|
0 |
|
0 |
|
0 |
|
1 |
|
0 |
|
0 |
|
0 |
|
|
0 |
|
0 |
|
3 |
|
||||||
13 |
|
1 |
|
0 |
|
0 |
|
0 |
|
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
|
0 |
|
|
1 |
|
|||||
Построим неориентированный граф G2, используя способ перечисления.
G2=(V2,E2):
V2={1,2,3,4,5,6,7,8,9,10,11,12,13} – множество вершин графа; E2={(1,12),(1,13),(2,3),(2,6),(2,9),(2,11),(3,5),(3,6),(3,11),(4,5), (4,8),(4,12),(6,7),(6,10),(6,11),(7,8),(7,10),(8,12)} – множество ребер графа.
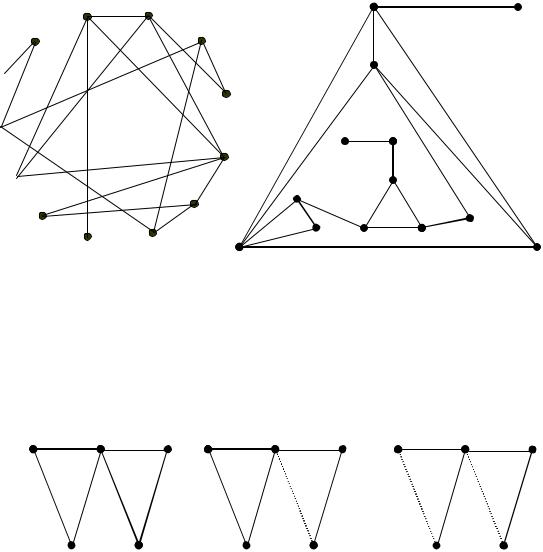
98
Построим графическое изображение графа G2.
G2: |
2 |
|
|
1 |
|
13
12 
11 
10
9
3 |
или: |
2 |
6 |
9 |
|
|
|
|
|
|
4 |
21 |
|
|
|
|
3 |
|
|
|
5 |
|
|
|
|
|
7 |
14 |
|
|
28 |
7 |
|
|
|
|
|
|||
|
|
|
|
13 |
18 |
1 |
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
14 |
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
7 |
18 |
7 |
21 |
|
6 |
12 |
|
|
|
|
|||||
|
12 |
|
30 |
|
|
6 |
5 |
|
|
10 |
8 |
|
4 |
7 |
|
8 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
14 |
11 |
|
|
|
|
|
|
|
2. Для произвольного остова графа G1 построить матрицу фундаментальных циклов. Посчитать циклический и ациклический ранг, выразить три непростых цикла (если таковые имеются) через минимальную комбинацию базисных.
|
Граф G1: |
|
|
Остов Т1: |
|
|
Остов Т2: |
|
1 |
2 |
3 |
1 |
2 |
3 |
1 |
2 |
3 |
4 |
5 |
4 |
5 |
4 |
5 |
| V | = p = 5, | E | = q = 6, k =1.
ν=q-p+k=6-5+1=2 – циклический ранг (хорды); ν*=p-k=5-1=4 – коциклический ранг (ветви).
Выпишем все циклы в графе G1: C1={1,2,4,1};
C2={2,5,3,2};
C3={2,1,4,2,5,3,2}.
Каждому циклу в графе G1 ставится в соответствие вектор длиной q. Обозначим этот вектор: z=(z1,z2,z3,…,zq):
z1=(1,1,0,1,0,0); z2=(0,0,1,0,1,1); z3=(1,1,1,1,1,1).
В графе G1 все имеется только один непростой цикл C3.
99
Выразим цикл С3 через базисные циклы С1 и С2: С3=С1 С2=(1,1,0,1,0,0) (0,0,1,0,1,1)=(1,1,1,1,1,1).
Матрица фундаментальных циклов:
Т |
(1,2) |
(1,4) |
(2,3) |
(2,4) |
(2,5) |
(3,5) |
|
|
|
|
|
|
|
C1 |
1 |
1 |
0 |
1 |
0 |
0 |
|
|
|
|
|
|
|
C2 |
0 |
0 |
1 |
0 |
1 |
1 |
|
|
|
|
|
|
|
C3 |
1 |
1 |
1 |
1 |
1 |
1 |
|
|
|
|
|
|
|
3. Определить, являются ли графы G1 и G2 эйлеровыми, построить эйлеровы циклы по алгоритму Флёри, эйлеровы цепи. Если граф не эйлеров, добавить минимальное число ребер, делающих его эйлеровым.
1)Рассмотрим граф G1: в нем все вершины имеют четную степень, следовательно, граф G1 имеет эйлеров цикл, то есть является эйлеровым графом.
1 |
2 |
3 |
4 |
5 |
Построим в графе эйлеров цикл с помощью алгоритма Флери. Задача сводится к поиску способа нумеровации всех ребер в полученном графе таким образом, чтобы номер каждого ребра указывал порядок вхождения ребра в цикл.
V |
(1,2) |
(1,4) |
(2,3) |
(2,4) |
(2,5) |
(3,5) |
|
|
|
|
|
|
|
№ |
1 |
2 |
4 |
3 |
6 |
5 |
|
|
|
|
|
|
|
№ |
4 |
5 |
3 |
6 |
1 |
2 |
|
|
|
|
|
|
|
Эйлеровы циклы: С1={2,1,4,2,3,5,2};
C2={2,5,3,2,1,4,2}.
Построим в графе эйлеровы цепи. Для этого удалим ребро (2,3), тогда только две вершины – 2 и 3 – будут иметь нечетную степень, а это является необходимым и достаточным условием того, что граф G1 покрывается эйлеровой цепью.
1 |
2 |
3 |
4 |
5 |
Эйлеровы цепи: P1={2,1,4,2,5,3}; P2={3,5,2,4,1,2}.
