
- •Ціль і задачі курсу
- •Самостійна робота
- •МАСИВИ
- •Рисунок 1. Ввід і вивід одномірного масиву
- •Рисунок 2. Ввід і вивід двовимірного масиву
- •Лабораторна робота №6
- •Лекція №10. ОСНОВИ РОБОТИ В MS EXCEL
- •Відображення
- •Об'єкт.Властивість=Вираз
- •14.3. Лабораторна робота №4
- •Тема: «Організація вкладених циклів»
- •Результати
- •Масив Х
- •Масив Y
- •Сума
- •Масив Х
- •Масив Y
- •Добуток
- •Властивість
- •Опис
- •Опис
- •Опис
- •Опис
- •Багаточлен другого ступеня.
- •Укладачі: Добровольський Юрій Миколайович
- •Єфіменко Костянтин Миколайович
28
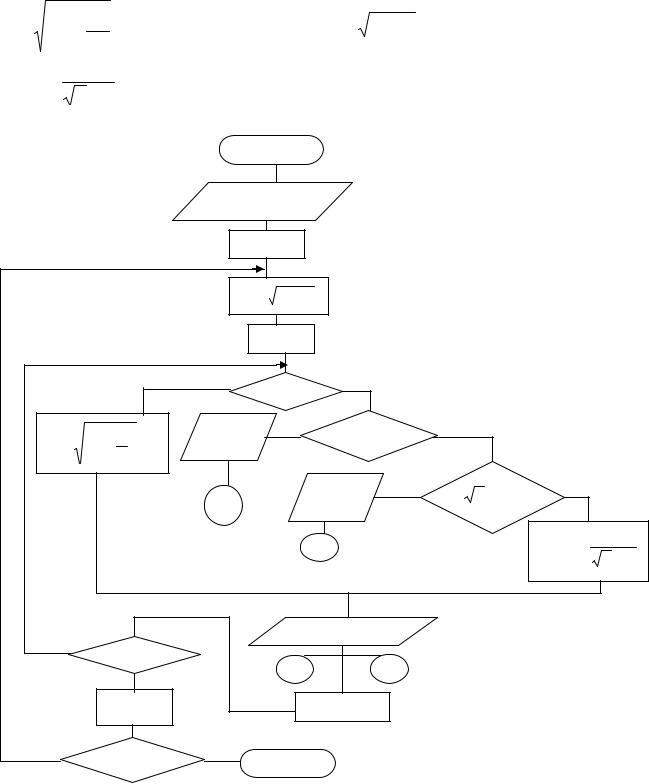
Лабораторна робота №4.
Тема: «Організація вкладених циклів»
При складанні блок-схем організувати цикли зпістумовою або із переду-
мовою, цикл “Для” можна організувати тільки в тому випадку, якщо змінна цик-
лу ціле число й крок дорівнює 1.
|
Самостійна робота |
|
|
|
|
|
|||||
ì |
x2 |
+ a |
2 |
+ x3 , |
|
|
|
, x = 3 4 + t 2 |
|
||
ï |
|
|
если |
x > 1,6 |
|
||||||
ï |
|
4 |
|
|
|
|
|
|
|
|
|
Z = í |
|
x |
|
|
|
|
|
|
|
|
|
ï |
|
|
, |
если |
x <= 1,6 |
|
|
|
|
||
ïa + |
|
|
|
|
|
|
|||||
î |
|
a - x |
|
|
|
|
|
|
|
||
Вихідні дані: 1,5£ a £ 2,5; ha=0,5 |
2£ t £ 4,5; |
ht=1 |
|
||||||||
Виведені дані: a, t, x, z. |
|
початок |
|
|
|
||||||
|
|
|
|
|
|
|
Ввід |
|
|
|
|
|
|
|
|
|
|
|
an,ak,ha,tn,tk,ht |
|
|
|
|
|
|
|
|
|
|
|
|
t=tn |
|
|
|
|
|
|
|
|
|
|
x = 3 4 + t 2 |
|
|
|
|
|
|
|
|
|
|
|
|
a=an |
|
|
|
|
|
|
|
|
|
- |
|
x£1,6 |
|
+ |
|
|
|
|
|
|
|
Корінь |
- |
|
+ |
|
|
|
|
|
|
+ a |
2 |
|
a³0 |
|
|||
|
z = |
x 2 |
+ x3 |
не існує |
|
|
|
|
|||
|
|
|
|
4 |
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
Ділен. |
|
|
|
|
|
|
|
|
В |
|
на 0 |
a ¹ x |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
А |
z = a + |
x |
|
|
|
|
|
|
|
|
|
a - x |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
Вивод a,t,x,z |
|
||
|
|
|
|
a>ak |
|
|
B |
|
A |
|
|
|
|
|
|
|
+ |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t=t+ht |
|
|
|
a=a+ha |
|
||
|
- |
|
|
t>tk |
|
+ |
кінець |
|
|
|
|
|
|
|
|
|
|
|
|
||||
29
Лекція №6.
ОРГАНІЗАЦІЯ ІТЕРАЦІЙНОГО ПРОЦЕСУ
Цикл називається ітераційним, якщо при кожному наступному виконанні циклу результат обчислення наближається до шуканого із заданою точністю.
Визначення 1. Функціональним рядом називається вираз вигляду:
¥
u1 (x) + u2 (x) +L+ un (x) +L = åui (x) , де u1(x),u2(x), …є функції одного аргу-
i =1
менту.
Якщо ui(x)=aixi – то ряд називається статечним.
Розглянемо часткові суми:
S1(x)=u1(x), S2(x)=u1(x)+u2(x),… , Sn(x)=u1(x)+u2(x)+…+un(x)
Визначення 2. Ряд називається збіжним(має суму), якщо послідовність його часткових сум має кінцеву межу.
|
|
n |
S (x) = lim Sn |
(x) = lim |
åui (x) |
n®¥ |
n®¥ |
i=1 |
|
|
Визначення 3. Сукупність тих значень ,х для яких функціональний ряд сходиться (має суму) називається областю збіжності цього ряду, а функція S(x)-
його сумою. Функціональний ряд у крапці перетворюється в числовий ряд.
Надалі аргумент х будемо опускати. S=u1+u2+…+un+…, S=Sn+un+1+un+2+…+… Rn=un+1+un+2+…+… - залишковий член ряду.
Якщо ряд сходиться, то й залишковий член ряду сходиться. S=Sn+Rn, Rn=S-
Sn.
Теорема. Якщо суму ряду замінити першимиn членами, то помилка, що ми отримуємо, не перевершує першого члена, що відкидає. (Якщо S»Sn ,те
|Rn|<un+1).
Якщо вибрати n так, що un+1£e, де e>0, то |Rn|<e, те говорять, що сума ряду
|
|
|
|
|
30 |
|
|
знайдена із заданою точністю e. |
|
|
|
||||
|
|
|
|
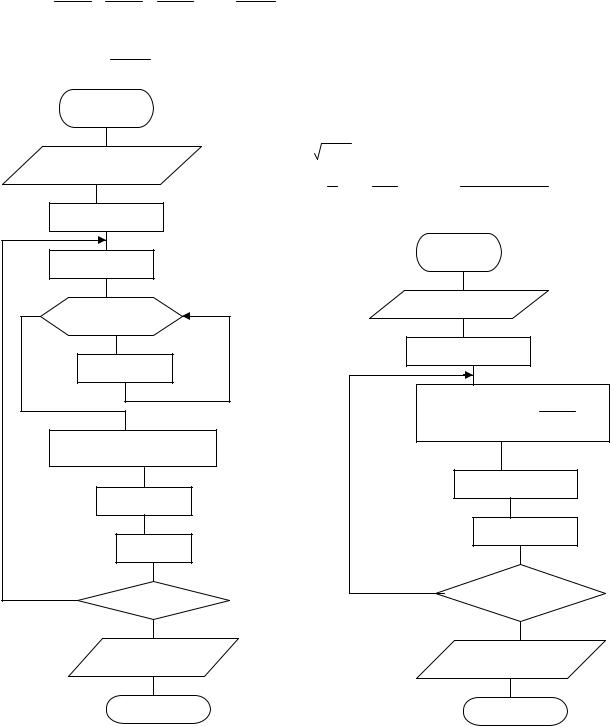
Лабораторна робота №5. |
|||
Тема: «Організація ітераційного процесу» |
|
||||||
Приклад №1. Обчислити значення функції y=2sin2x, як знаходження суми |
|||||||
ряду: |
|
|
|
|
|
|
|
y = (2x)2 |
- (2x)4 |
+ (2x)6 |
-L± (2x)2i |
mL с заданою точністю e=0,001; х=0,5 |
|||
2! |
4! |
|
6! |
(2i)! |
|
|
|
ui = (-1)i+1 × (2x)2i |
- загальний член ряду. |
|
|
||||
|
(2i)! |
|
|
|
|
|
|
початок |
|
|
|
|
|
|
|
|
|
|
|
|
Приклад №2. (Вар. №1) |
||
Ввід x,e |
|
|
|
y = 33 1 + x - 3 |
|
||
|
|
|
y = x - 2 x 2 + 2 ×5 x3 -L ± 2 ×5L(3i - 4) xi mL |
||||
|
|
|
|
|
|||
|
|
|
|
|
6 |
6 ×9 |
6 ×9L3i |
i=1, S=0 |
|
|
|
|
|
|
|
|
K=1 |
|
|
|
|
|
початок |
|
|
|
|
|
|
|
|
|
j=1,2*i |
|
|
|
|
|
Ввід x,e |
|
|
|
|
|
|
|
|
|
k=k*j |
|
|
|
|
|
i=2,s=x,p=x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p = (-1)2i-1 * p * 3i - 4 * x |
|
|
|
|
|
|
|
3i |
ui = (-1)i+1 * (2x)2i / k |
|
|
|
||||
|
s=s+ui |
|
|
|
s=s+p |
||
|
|
|
|
|
|||
|
i=i+1 |
|
|
|
i=i+1 |
||
|
|
|
|
|
|||
- |
|ui|<e |
|
|
- |
|p|<e |
||
|
|
|
|
|
|||
|
|
|
+ |
|
|
|
+ |
|
|
|
|
|
|
|
|
Вивод x,e,s |
Вивод x,e,s |
кінець |
кінець |
31
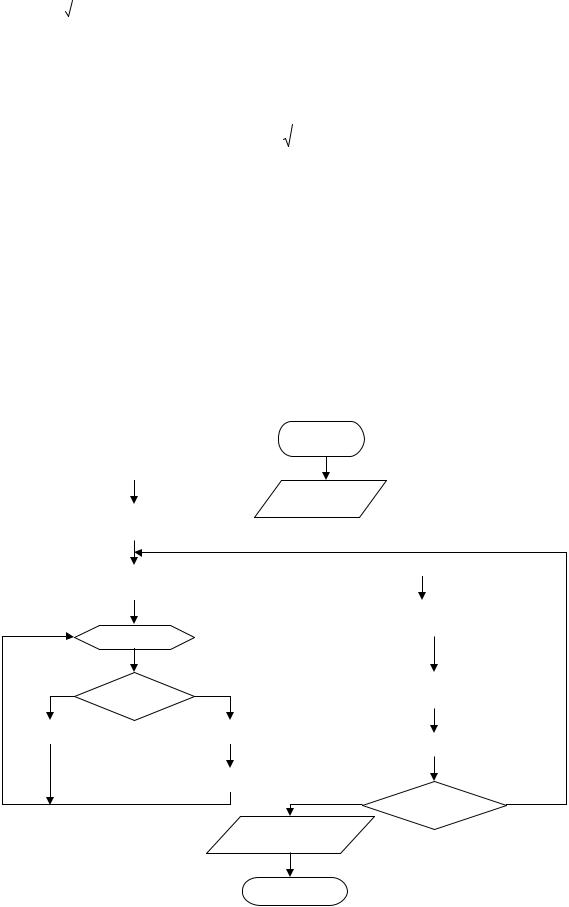
Приклад №3. (Вар №6)
y = 1 - |
1 |
y = |
1 |
x - |
1× 4 |
x 2 + |
1× 4 ×7 |
x3 -L± |
1× 4 ×7L(3i - 2) |
xi m L |
|
|
|
|
|
|
|
||||||
|
3 1 + x |
3 |
3 ×6 |
3 ×6 ×9 |
|
3 ×6 ×9L3i |
|||||
Початкові значення параметрів: i=1,s=0,p=-1 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
Рекурентна формула: |
p = (-1) × p × |
|
(3i - 2) |
x, |
s = s + p, i = i +1 |
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Приклад №4. (Вар №7) |
|
|
48 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
y = |
( (x + 5)5 |
-1) - 8x - 6x 2 |
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
x3 - |
1 |
x 4 + |
1×3 |
x5 - |
1×3 ×5 |
|
x 6 +Lm |
|
|
1×3 ×5L(2i - 3) |
xi +2 ±L |
|
||||||||||||||||||||||||||||||||||
|
8 ×10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
8 |
|
|
|
|
8 ×10 ×12 |
|
|
|
|
|
|
8 ×10 ×12L2(i + 2) |
|
||||||||||||||||||||||||||||||||||
Початкові значення параметрів: i = 2, |
s = x3 , |
p = x3 , |
|
||||||||||||||||||||||||||||||||||||||||||||
Рекурентна формула: |
p = (-1) * p * |
2i - 3 |
|
|
* x, s = s + p, i = i +1 |
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2(i + 2) |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Приклад №5. (Вар №2). |
|
y = x sin x - e- x 2 |
+1 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
y = x2 ( |
1 |
+ |
|
1 |
) - x4 ( |
1 |
+ |
1 |
) + L± x2i ( |
1 |
+ |
|
1 |
|
|
) m L |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
1! |
1! |
|
2! |
3! |
|
|
|
|
|
|
|
|
|
i! (2i -1)! |
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
початок |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ввід x, e |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
i=1 |
s=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
P1=1 |
P2=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
j=1,2*i-1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ui = (-1)i+1 * x 2i ( |
1 |
|
+ |
1 |
) |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
- |
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p1 p2 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
j<=i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s = s + ui |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P2=P2*j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P1=P1*j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i=i+1 |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P2=P2*j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|ui|<e |
- |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Вивод x,e,s
кінець
32
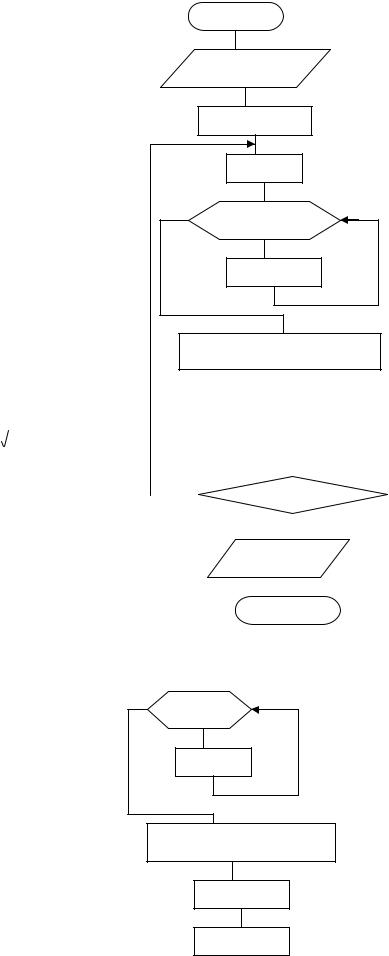
Приклад №6. (Вар. №3) y=sinx-cosx+1
y = |
x(2 + x) |
- |
x3 |
(4 + x) |
+ |
x5 |
(6 + x) |
-L± |
x 2i-1 (2i + x) |
|
|
|
|
|
|
|
mL |
||||
2! |
|
4! |
|
6! |
|
|||||
|
|
|
|
|
|
(2i)! |
||||
Приклад №7. (Вар. №4) |
y = 1 - |
|
|
1 |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
4 1 + x |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
y = |
1 |
x - |
1×5 |
x 2 + |
1×5 ×9 |
x3 -L± |
1×5 ×9L(4i - 3) |
xi m L |
|
|||||||||||||||||||
4 |
|
|
|
|
4 ×8 ×12L4i |
|
||||||||||||||||||||||
|
|
4 ×8 |
|
|
4 ×8 ×12 |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
æ 4i - 3 ö |
|
|
|
|||||||
i = 1, s = 0, |
|
p = -1, |
p = (-1) * p *ç |
|
|
|
|
|
÷ * x, |
s = s |
+ p, |
|||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è |
|
|
4i ø |
|
|
|
||||||
Приклад №8. (Вар. №5) |
|
y = |
1 - cos x + x sin x |
+ 0,5 |
||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 2 |
|
|
|
y = |
3x 2 |
|
|
5x 4 |
|
|
7x 6 |
9x8 |
|
(2i +1) |
× x 2i |
|
|
|
||||||||||||||
|
|
- |
|
|
+ |
|
|
- |
|
|
+L± |
|
|
|
|
|
|
|
m L |
|
|
|
||||||
4! |
6! |
|
8! |
10! |
|
(2i + |
2)! |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
початок
Ввід x,e
i=1,s=0
k=1
j=1,2i
k=k*j
ui = (-1)i+1 * x 2i-1 (2i +1) / k
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s=s+ui |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i=i+1 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|ui|<e |
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
i = i +1 |
|
|
|
|
+ |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
Вивод x,e, s |
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
i=1,s=0 |
|
|
|
кінець |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
K=1 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
J=1,2i+2 |
k=k*j |
ui = (-1)i+1 (2i +1) × x 2i / k
s=s+ui
i=i+1
