2. Задание и порядок выполнения лабораторной работы

Исследовать переходной процесс на выходе схемы, представленной на рис.2., при замыкании ключа К. Начальные условия U_c(0_-) = 0 и I_L(0_-) = 0. Варианты заданий взять из таблицы 1.

Построить графики изменения выходного напряжения от времени. Значение постоянного напряжения Е численно равно номеру варианта. В качестве выходной величины взять для группы А напряжение U_b, группы Б - U_ab, группы В - U_a, группы Г - ток через элемент Z_4. R₁=1 Ком, R₂=2 Ком, L₁=0,1 Гн, L₂=0,2 Гн, С₁= 1мкФ, С₂= 2 мкФ.

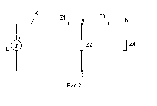
Таблица 1

№ вар	Z1	Z2	Z3	Z4	№ вар	Z1	Z2	Z3	Z4
1	R1	L1	C2	R2	14	R2	R2	L1	C2
2	R2	C1	L2	R1	15	L1	R1	C1	R1
3	L1	R1	C2	R2	16	L2	R2	C1	R2
4	L2	C1	R2	R1	17	C1	R1	L1	R1
5	C1	R1	L1	R2	18	C2	R2	R1	L2
6	C2	L2	R2	R1	19	R1	C1	L2	R1
7	R1	R2	L1	C2	20	R2	L2	R2	C2
8	R2	R1	C1	L2	21	L1	R2	R1	C2
9	L1	R1	R2	C2	22	R2	C2	R1	C2
10	L2	R2	C1	R1	23	C1	L1	R2	R1
11	C1	R1	R2	L1	24	C2	R1	R1	L1
12	C2	R2	L2	R1	25	R1	L1	C2	R1
13	R1	L1	R2	C2	26	R2	C2	L1	R2

3. Пример выполнения задания

Пусть требуется определить изменение во времени напряжения на емкости схемы, показанной на рис.3. Величины элементов приведены на схеме. Начальное напряжение на емкости и начальный ток через индуктивность равны нулю.

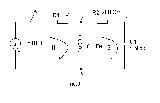
Составим уравнение электрической цепи, представленной на рис.3. Для этого можно использовать, например, методы Кирхгофа, узловых потенциалов, контурных токов. Воспользуемся методом контурных токов

,

.

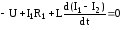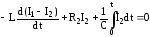Для упрощения преобразования уравнений введем операторы дифференцирования и интегрирования.

; .

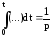Над операторами можно совершать все алгебраические операции. Запишем полученные уравнения в операторном виде

(1)

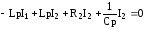(2)

Найдем I₂₂. Для этого из уравнения (1) выразим I₁ через I₂ 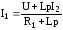и подставим его в уравнение (2). В результате получим

.

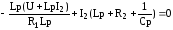Отсюда найдем

. (3)

Напряжение на емкости равно . Поэтому, разделив выражение (3 ) наpC получим напряжение на емкости

.

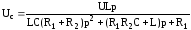Запишем это уравнение в виде операторного уравнения

,

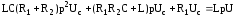где р – оператор дифференцирования. Заменяя р на 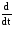запишем уравнение в обычном виде

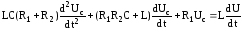. (4)

Подставим в уравнение значения элементов

.

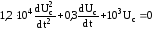Так как входное напряжение U постоянное равное 10 В, то правая часть уравнения будет равна 0.

Решение уравнения состоит из двух частей собственной или переходной составляющей и вынужденной или установившейся составляющей. Собственную составляющую решения найдем из решения однородного уравнения (4). Характеристическое уравнение имеет вид

,

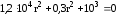а его корни равны .

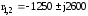Свободная составляющая напряжения на емкости будет равна

,

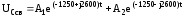где А₁ и А₂ постоянные интегрирования, которые находятся из общего решения уравнения (4).

Вынужденная составляющая решения определяется для бесконечного времени. Индуктивность в этом случае можно рассматривать как замкнутую цепь. Точки a и с можно считать соединенными, а емкость закороченной через сопротивление R₂. Следовательно, напряжение на емкости будет равно нулю. Поэтому общее решение уравнения (4) будет иметь вид

. (5)

В решение уравнения входят две постоянные интегрирования А₁ и А₂ . Для их нахождения необходимо еще одно уравнение. Для этого найдем ток, протекающий через емкость. Учитывая, что ток через емкость определяется из выражения 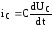, найдем свободную составляющую тока

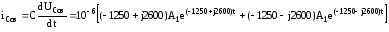Вынужденная составляющая решения тока очевидно равна 0, так как равна нулю вынужденная составляющая напряжения на емкости. Итак ток через емкость будет равен

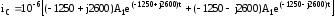. (6)

Постоянные интегрирования найдем из уравнений (5) и (6), записав их для нулевого момента времени. Начальное значение напряжения на емкости по условию равно нулю. А начальное значение тока через емкость необходимо еще определить. Для нулевого момента времени с учетом, что начальные значения тока индуктивности и напряжения емкости равны нулю, можно считать цепь с емкостью замкнутой, а цепь с индуктивностью разомкнутой. Тогда, в нулевой момент времени ток течет только через сопротивления R₁ и R₂.

.

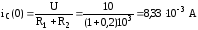Для нулевого момента времени уравнения (5) и (6) имеют вид

.

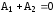
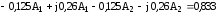Решая систему уравнений, получим

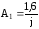и .

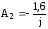Подставляя найденные значения в формулу (5) с учетом формулы Эйлера запишем напряжение на емкости

.
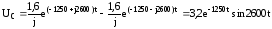