9

Основы электротехники и электроники Лабораторная работа n 3 Исследование переходных процессов в электрических цепях

Цель работы: привить практические навыки исследования динамики электрических цепей

1. Теоретическая часть

Цепи, содержащие L-и (или) С- элементы, описываются системами линейных интегродифференциальных уравнений. В отличие от резистивных цепей, где форма реакции известна (она подобна форме воздействия), здесь закон изменения реакции во времени неизвестен - он должен быть найден из решения дифференциальных уравнений цепи, удовлетворяющих начальным условиям.

Решая дифференциальные уравнения динамики цепи известными методами можно получить аналитические выражения зависимости реакции цепи на входное воздействие. Однако, аналитическое решение дифференциальных уравнений сопряжено с большими вычислительными трудностями, особенно для уравнений высокого порядка. Получаемые при этом аналитические выражения трудны для анализа. Поэтому, для анализа электрических систем, часто используют моделирование на аналоговых и цифровых вычислительных машинах. При использовании ЦВМ осуществляется численное решение дифференциальных уравнений цепи. Результат моделирования выводится на экран в виде кривых динамических процессов. Для выполнения лабораторной работы используется система моделирования MCAP-3 или MCAP-5.

В дополнение к резистивным элементам и источникам сигналов добавим элементы, запасающие энергию, - индуктивности и емкости. Вольт-амперные характеристики этих элементов, в отличие от резистивных, включают в себя операции дифференцирования и интегрирования:

индуктивность: u = L di/dt; i = (1/L) udt;

емкость: i = C du/dt; u = (1/C)idt.

Цепи, содержащие L-и (или) С- элементы, описываются системами линейных интегродифференциальных уравнений. Изменения режимов работы цепи (переходные процессы) вызываются коммутациями в цепи или изменением параметров ее элементов.

Начальные условия интересующих переменных определяются по независимым начальным условиям, которые задаются в виде напряжений u_C(0-) емкостей и токов i_L(0-) индуктивностей.

Напряжения (заряды) емкостей и токи (потокосцепления) индуктивностей при конечных значениях амплитуд токов и напряжений являются непрерывными величинами - не могут изменяться скачком. В связи с этим можно сформулировать два закона коммутации.

Первый закон коммутации.

Ток через индуктивность непосредственно до коммутации i_L(0-) равен току через ту же индуктивность непосредственно после коммутации i_L(0+):

i_L(0-) = i_L(0+).

Второй закон коммутации.

Напряжение на емкости непосредственно до коммутации u_C(0-) равно напряжению на той же емкости непосредственно после коммутации u_C = (0+):

u_C(0-) = u_C(0+).

Итак, токи через индуктивности и напряжения на емкостях непосредственно после коммутации всегда равны их значениям непосредственно до коммутации. Остальные величины: напряжения на индуктивностях, токи через емкости, токи и напряжения на активных сопротивлениях- могут изменяться скачком, и потому их значения непосредственно после коммутации чаще всего оказываются не равными их значениям до коммутации.

Поэтому следует различать докоммутационные и послекоммутационные начальные значения.

Докоммутационными начальными значениями называются значения токов и напряжений непосредственно до коммутации (при t = 0-); послекоммутационными начальными значениями - значения токов и напряжений непосредственно после коммутации (при t=0+).

Для любой схемы после коммутации в ней можно записать уравнения по законам Кирхгофа; из этих уравнений определить значения токов во всех ветвях и напряжения на любых участках схемы в послекоммутационном режиме. (при t=0+).

С этой целью значения токов в ветвях, содержащих индуктивности, и значения напряжений на конденсаторах берут равными тем значениям, которые они имели до коммутации при t = 0-, а остальные токи и напряжения после коммутации при t =0+ находят из уравнений Кирхгофа, поскольку часть слагаемых в них известна.

Значения токов через индуктивности и напряжений на емкостях, известные из докоммутационного режима, называются независимыми начальными значениями.

Значения остальных токов и напряжений при t= 0+ в послекоммутационной схеме, определяемые по независимым начальным значениям из законов Кирхгофа, называются зависимыми начальными условиями

Анализ динамических цепей начинают с составления системы дифференциальных и алгебраических уравнений на основе соединений цепи и уравнений элементов. Можно применить метод узловых напряжений, контурных токов. Часто требуется нахождение не всех, а одной или пары реакций цепи, т.е. проведение анализа по “входу - выходу”. Для определения интересующей реакции систему исходных дифференциальных уравнений путем исключения остальных переменных приводят к одному линейному уравнении n- го порядка с постоянными коэффициентами:

dⁿi/dtⁿ + b_n-1d^n-1/dt^n-1 + ... + b₁di/dt + b₀i_n = f(t), (4.1) где i = i(t) - выходная реакция; f(t)- правая часть, состоящая в общем случае из суммы слагаемых, пропорциональных воздействию и его производным. Необходимо найти решение уравнения, удовлетворяющее заданным начальным условиям.

Общее решение ЛДУ ищут в виде суммы двух составляющих:

i = i_св + i_в, (4.2)где i_св - свободная составляющая решения, а i_в - вынужденная составляющая.

а) Свободная составляющая решения i_св представляет общее решение однородного уравнения, получающегося приравневанием нулю правой части (1.1):

dⁿi/dtⁿ + b_n-1d^n-1/dt^n-1 + ... + b₁di/dt + b₀i_n = 0. (1.3)

Решение (1.3) ищут в виде экспоненты i_св = Аexp(pt). После подстановки экспоненты и ее производных в (1.3) получают алгебраическое уравнение степени n , называемое характеристическим уравнением

pⁿ + b_n-1p^n-1 + ... + b₁p + b₀ = 0. (1.4)

Каждый из n корней этого уравнения дает независимое решение А_кexp(p_кt); общее решение однородного уравнения будет линейной комбинацией этих решений.

Если корни p_к характеристического уравнения различны, то общее решение имеет вид

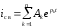, (1.5)

где А_к - произвольные постоянные.

При наличии в характеристическом уравнении кратных корней общее решение будт содержать слагаемые в виде экспонент с множителями - полиномами от t степени m-1, где m - кратность корня. Если p₁ является m - кратным корнем, а остальные корни - простые, то

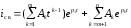. (1.6)

Как видно из (1.5) и (1.6), общий вид свободной составляющей известен, если известны значения p_к. Произвольные постоянные А_к должны быть определены таким образом, чтобы были удовлетворены начальные условия.

Физический смысл свободной составляющей. Равенство нулю правой части ДУ означает отсутствие внешнего воздействия на цепь - удаление и короткого замыкания выводов всех источников напряжения, удаление и разрыв выводов всех источников тока. Следовательно цепь свободна от внешних сигналов и предоставлена самой себе, так что реакции - токи и напряжения - будут определяться только параметрами и свойствами самой цепи, а также начальным запасом энергии - появление токов и напряжений возможно только за счет ранее запасенной энергии в индуктивностях и емкостях.

Свободную составляющую называют собственными колебаниями, а определяющие их корни характеристического уравнения - частотами собственных колебаний.

б) Вынужденная составляющая решения i_в представляет частное решение неоднородного уравнения (с правой частью) (1.1). Вид частного решения зависит от правой части уравнения, т.е. от вида приложенного к цепи сигнала, который принудительно устанавливает эту составляющую реакции; отсюда ее название. В случае сигнала произвольной формы определение вынужденной составляющей реакции связано с большими трудностями. Лишь в случае простых, но важных в теории цепей форм сигналов - экспоненциальных, гармонических, степенных - вид частного решения получается подобным правой части уравнения: вынужденные составляющие имеют соответственно вид экспонент, гармонических функций той же частоты и степенных функций (полиномов), но с неизвестными коэффициентами или параметрами. Для нахождения последних принятые функции подставляют в уравнение (1.1) и приравнивают коэффициенты левой и правой частей. При высоком порядке уравнений отыскание частного решения по указанному способу неопределенных коэффициентов получается довольно громоздким. Лишь при воздействии постоянного сигнала (полинома нулевого порядка) вынужденная реакция, также постоянная, все производные которой равны нулю, определяется предельно просто. Постоянную, а также любую периодическую вынужденную составляющую называют установившейся составляющей реакции.

Следует отметить, что указанное подобие частного решения и правой части в виде рассмотренных простых функций нарушается, когда корни p_к характеристического уравнения принимают определенные значения. Если p_к = 0- корень кратности m, то при постоянной правой части вынужденная реакция i_в = А_кt^m-1 не является установившейся, так же как при корне p_к = jw и воздействии сигнала u = U_mcos(t + _u), когда вынужденная реакция i_в= Аtcos(t + _i).

Общее решение уравнения (1.1)

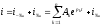содержит n произвольных постоянных А_к. Для получения единственного решения определяют произвольные постоянные так, чтобы были удовлетворены n начальных условий в виде значений искомой функции и ее n-1 производных при t = 0 : i(0); i’(0), i’’(0); ... ; i^n-1(0).

Приведенная общая схема анализа динамических цепей во временной области на основе решения дифференциального уравнения называют классическим методом анализа цепей.

Наряду с анализом цепи путем сведения системы исходных уравнений к одному уравнению относительно интересующей реакции, которой можно назвать анализом на основе подхода “вход- выход”, применяют анализ по уравнениям переменных состояния как более общего подхода.

Пример

t=0 L R i + + C U - -

Цепь из последовательно соединенных элементов L, R, C, подключаемую в момент времени t = 0 к источнику постоянного напряжения, показана на рис 1. В качестве независимых начальных условий должны быть заданы i_L(0), u_C(0).

u_L + u_R + u_C = U.

Ldi/dt + Ri + (1/C)idt = U (t>t). (1.10)

Продифференцировав 1.10 получим ОДУ

Ld²i/dt² + Rdi/dt + (1/C)i = 0 (t>0). (1.11)

Решение ищем в виде

i = i_св +I_в.

Вынужденная или установившаяся составляющая тока в цепи при действии постоянного напряжения, очевидно, равна нулю, поскольку в цепи имеется последовательная емкость. Следовательно i_у = 0, u_Cу = U.

Свободная составляющая является общим решением уравнения при нулевой правой части (короткозамкнутом входе)

Ld²i_св /dt² + Rdi_св /dt + (1/C)i_св = 0.

Характеристическое уравнение

p² + (R/L)p + (1/LC) = p² + 2p + ₀² =0,

где = R/(2L) - коэффициент затухания; ₀ = 1/(LC)^1/2 - угловая резонансная частота.

Оба параметра, определяющие характеристическое уравнение, выражаются с^-1. Характеристическое уравнение имеет два корня, а контур - две частоты собственных колебаний

p_1,2 = - (² - ₀²)^1/2.

Вид корней или частот собственных колебаний зависит от подкоренного выражения или от отношения

/₀ = R/2(L/C)^1/2 = R/(2) = 1/2Q,

где = (L/C)^1/2 - характеристическое сопротивление контура; Q = /R - добротность контура, равная отношению характеристического сопротивления к сопротивлению резистивного элемента. В обычно применяемых контурах Q = 50 300.

Через введенные параметры корни можно представить в виде

.

При изменении добротности в пределах 0 Q возможны следующие виды корней:

1) Q = ; R=0; = 0 - корни мнимые комплексно сопряженные; свободная составляющая имеет вид гармонических колебаний.

2) Q > 1/2; Q = ₀/2 > 1/2; ₀ > ; R < 2 - корни комплексные сопряженные с отрицательной действительной частью; свободная составляющая имеет вид затухающих колебаний.

3) Q = 1/2; ₀ = ; R= 2 - корни вещественные отрицательные, равные - критический режим.

4) Q < 1/2; > ₀; R > 2 - корни вещественные отрицательные, неравные - апериодический режим.

Каждый из корней дает независимое решение, поэтому свободная составляющая тока в цепи

i_св = A₁exp(p₁t) + A₂exp(p₂t), (1.12)

где А₁, A₂ - произвольные постоянные интегрирования.

Для определения двух постоянных из начальных условий необходимо иметь выражение производной или интеграла от (1.12).

u_Cсв = (1/C)i_свdt = (A₁/Cp₁)exp(p₁t) + (A₂/Cp₂)exp(p₂t).

Просуммировав свободную и установившуюся составляющие, получим выражения для тока и напряжения на емкости при воздействии на цепь постоянного напряжения:

i = A₁exp(p₁t) + A₂exp(p₂t) + 0;

u_C = (A₁/Cp₁)exp(p₁t) + (A₂/Cp₂)exp(p₂t) + U.

Примем следующие начальные условия в цепи: i_L(0) = 0; u_C(0) = U₀.

Из условий при t=0 имеем 0 = А₁ + А₂

U₀ = A₁/(Cp₁) + A₂/(Cp₂) + U.

Отсюда находим постоянные интегрирования

А₁ = - А₂ = С(U - U₀)p₁p₂/(p₁ - p₂). (1.13)

Значения постоянных интегрирования существенно зависят от вида корней характеристического уравнения, определяющих различные режимы в контуре.

Колебательный режим

Представим корни p_1,2 = - (² - ₀²)^1/2

в виде

p_1,2 = - j(₀² - ²)^1/2 = - j_d, (1.14)

где _{d =} (₀² - ²)^1/2, ₀² _{= d}² + ².

Отсюда получим p₁ - p₂ = j2_d; p₁p₂ = ₀². Подставим полученные выражения в формулу для постоянных интегрирования (1.13)

А₁ = - А₂ = С(U - U₀)p₁p₂/(p₁ - p₂) = С(U - U₀)₀²/(j2_d) = С(U - U₀)₀/((j2_d)(LC)^1/2)

А₁ = - А₂ = ((U - U₀)/) (₀/((j2_d)). (1.15)

Ток в контуре с учетом (1.14) и (1.15)

i = ((U - U₀)/) (₀/((j2_d)) exp(-t)(exp(j_dt) - exp(-j_dt)).

Используя формулу Эйлера, имеем

i = ((U - U₀)/) (₀/_d) exp(-t)sin(_dt).

Запишем угловую частоту колебаний с учетом /₀ = 1/(2Q)

_{d =} (₀² - ²)^1/2 = ₀(1- (1/2Q)²)^1/2.

При наличии потерь (конечной добротности) частота колебаний тока меньше резонансной частоты, которая равна частоте колебаний без потерь ( с бесконечной добротностью).

Затухание тока определяется множителем - экспонентой. Относительное затухание колебаний характеризуется декрементом затухания, представляющим отношение мгновенных значений тока через один период:

= exp(-t) sin(_dt)/ exp(-(t+T)) sin(_dt+T) = exp(T).

Натуральный логарифм декремента затухания называется логарифметическим декрементом: ln = T = 2_d.

Процессы в контуре без потерь.

При отсутствии потерь и бесконечной добротности контура свободная составляющая реакций не затухает. В этом случае = 0, p_1,2 = j_0.

i = A₁exp(p₁t) + A₂exp(p₂t).

А₁ = - А₂ = С(U - U₀)p₁p₂/(p₁ - p₂).

p₁p₂ = ₀²; p₁ + p₂ =j2.

А₁ = - А₂ = C(U - U₀) (₀/((j2)) = (U - U₀)/(j2).

i = (U - U₀)/(j2)(exp(j₀t) - exp(-j₀t)).

i = ((U - U₀)/)sin(₀t).

Учитывая, что u_c = (i/C)i_cdt + u_c(0), получим напряжение на емкости

u_C = U - (U-U₀)cos_ot.

При нулевом внешнем воздействии, т.е. при короткозамкнутом входе и действии в контуре начального напряжения на емкости U₀, имеем

i = - (U₀/)sin₀t; u_C = U₀cos₀t.

Амплитудные значения энергии в индуктивности и емкости получаются одинаковыми:

w_L = (Li²)/2 = (LU₀²)/(2²)sin²(₀t) = CU₀²/2 sin²(₀t);

w_C = CU₀² /2 cos²(₀t),а их сумма остается неизменной во времени и равной начальной энергии, запасенной в емкости: w_L + w_C = CU₀²/2.

Таким образом, с энергетической точки зрения процесс собственных колебаний в контуре без потерь состоит в периодическом обмене энергией между емкостью и индуктивностью. в момент максимума напряжения на емкости ток в контуре равен нулю ( вся энергия запасена в емкости), а в моменты максимума тока в контуре напряжение на емкости равна нулю (вся энергия запасена в индуктивности).

Апериодический режимы.

Апериодическому режиму соответствуют два различных отрицательных действительных корня характеристического уравнения:

p_1,2 = - (² - ₀²)^1/2 = - (< ).

p₁p₂ = ² - ² = ₀²; p₁ - p₂ = 2.

Постоянные интегрирования

А₁ = - А₂ = C(U - U₀) ₀²/(2) = (U - U₀) /(2L),

т.к. ₀² = 1/ (LC).

Ток в контуре будет равен

i = (U - U₀) /(2L) [ exp(-( - )t) - exp(-( + )t)]. (1.16)

Критический режим.

Критический режим соответствует двукратному корню p₁ = p₂ = - ; = 0. Его можно свести к рассмотренному апериодическому режиму. Переписав (1.16) и раскрывая неопределенность по правилу Лопиталя, получим

i = (U - U₀) /(2L) exp(-t)[ exp(t) - exp(- t)] = ((U - U₀)/L)texp(-t).

Здесь появляется характерный для случая двухкратных корней множитель t в экспоненте.