1.12. Объектно-ориентированные средства ввода-вывода.

Описание объектов для управления вводом-выводом содержится в заголовочном файле iostream.h.

При подключении этого файла с помощью директивы

#include <iostream.h>

в программе автоматически создаются объекты-потоки³

• cin для ввода с клавиатуры,

• cout для вывода на экран,

а так же операции

• помещения в поток <<,

• чтения из потока >>.

С помощью объекта cin и операции >> можно присвоить значение любой переменной.

Например, если переменная i описана как целочисленная, то команда

cin>>i;

означает, что в переменную i будет записано некое целое число, введенное с клавиатуры.

Если нужно ввести несколько переменных, следует написать

cin>>x>>y>>z;.

Объект cout и операция << позволяют вывести на экран значение любой переменной или текст.

Текст необходимо заключать в двойные кавычки.

Допустимо применение специальных символов

• \t - табуляция

• \n – перевод на новую строку.

Запись cout<<i; означает вывод на экран значения переменной i.

Команда

cout<<x<<”\t”<<y;

выведет на экран значения переменных x и y разделенные символом табуляции.

ЗАДАЧА 2. Известны плотность , высота h и радиус основания R цилиндрического слитка, полученного в металлургической лаборатории. Найти объем V, массу m и площадь S основания слитка.

Входные данные: , h, R.

Выходные данные: S, V, m.

Учитывая, что S=2R, V=R²h и m=V составим текст программы:

#include "stdafx.h"

#include <iostream.h>

//Опред. константы

#define pi 3.14159

int main()

{

double R,h,r,S,V,m;

cout<<"R=";

cin>>R;

cout<<"h=";

cin>>h;

cout<<"r=";

cin>>r;

S=2*pi*R;

V=pi*R*R*h;

m=r*V;

cout<<"S="<<S;

cout<<"\n V="<<V;

cout<<"\n m="<<m;

}

2. Операторы управления

Решение любой задачи на ЭВМ разбивают на следующие этапы:

• разработка алгоритма;

• составление программы на алгоритмическом языке;

• ввод программы в ЭВМ;

• отладка программы;

• выполнение программы;

• анализ результатов.

2.1. Понятие алгоритма

Алгоритм – четкое описание последовательности действий, которые необходимо выполнить при решении задачи (иначе, алгоритм – описание процесса преобразования исходных данных в результаты).

Разработка алгоритма решения задачи – это разбиение задачи на последовательно выполняемые этапы.

Способы представления алгоритмов:

• на естественном языке;

• в виде блок-схемы;

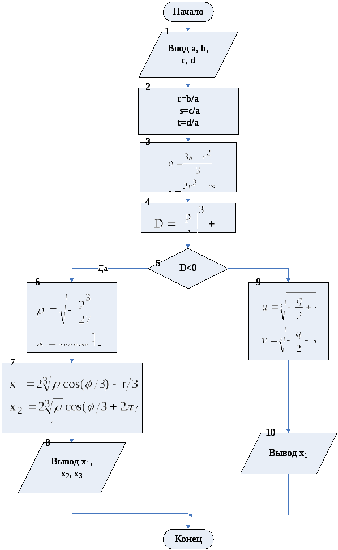
2.2. Изображение алгоритма в виде блок-схемы

Блок-схемой называется наглядное графическое изображение алгоритма.

В блок-схеме отдельные этапы алгоритма изображают при помощи различных геометрических фигур – блоков.

Последовательность выполнения этапов указываются при помощи стрелок, соединяющих эти фигуры. Блоки сопровождаются надписями.

Типичные действия алгоритма изображаются следующими геометрическими фигурами:

Блок начала (конца) алгоритма

Надпись: «начало» («конец»).

Блок ввода-вывода данных

Надпись: «ввод» («вывод»)

и список переменных вводимых (выводимых).

Блок решения (арифметический)

Надпись: операция или группа операций.

Условный блок

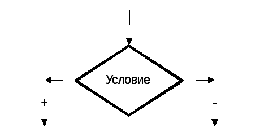
Надпись: логическое условие.

2.3. Составной оператор

Это группа операторов, отделенных друг от друга точкой с запятой, начинающихся с открывающей фигурной скобки { и заканчивающихся закрывающейся фигурной скобкой }.

{

оператор_1;

...

оператор_n

}

Транслятор воспринимает составной оператор как один оператор.

2.4. Операторы ветвления

Алгоритмы разветвленной структуры применяются, когда в зависимости от некоторого условия необходимо выполнить либо одно, либо другое действие.

Условный оператор, соответствующий приведенной блок-схеме, имеет вид:

if (выражение) оператор_1;

else оператор_2;

Вычисляется выражение. Если оно не равно нулю, т.е. имеет значение true, выполняется оператор_1, в противном случае (выражение равно нулю, т.е. false) – оператор_2.

Если в зависимости от некоторого условия выполняется некоторое действие, а в противном случае ничего не происходит, то алгоритм имет вид:

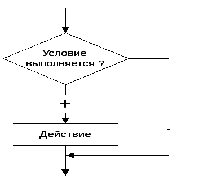
Условный оператор в этом случае имет конструкцию:

if (выражение) оператор;

Эту запись можно назвать «пропуск оператора else».

Здесь оператор либо выполняется, либо пропускается, в зависимости от значения выражения.

Если в какой-либо ветви условного процесса требуется выполнить несколько операторов, следует использовать составной оператор.

2.5. Примеры программ

Задача 2. Известны коэффициенты а, b и с квадратного уравнения ax²+bx+c=0. Вычислить корни квадратного уравнения.

Входные данные: a, b, c.

Выходные данные: х₁, х₂.

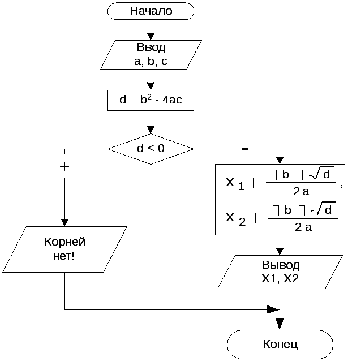
#include <stdio.h>

#include <math.h>

void main()

{

float a,b,c,d,x1,x2;

printf("\n vvedite a \n");

scanf("%f",&a);

printf("\n vvedite b \n");

scanf("%f",&b);

printf("\n vvedite c \n");

scanf("%f",&c);

d=b*b-4*a*c;

if (d<0) printf("reshenij net \n");

else

{

x1=(-b+sqrt(d))/(2*a);

x2=(-b-sqrt(d))/2/a;

printf("x1=%f \n", x1);

printf("x2=%f \n", x2);

}

}

Задача 2. Решить ax⁴+bx²+c=0 биквадратное уравнение (y=x²).

Дано: a,b,c.

Найти: х₁, х₂, х₃, х₄.

Алгоритм:

1. Вычисление дискриминанта уравнения d.

2. Если d  0, определяются y₁ и y₂, а иначе корней нет.

3. Если y₁, y₂ < 0 , то корней нет.

4. Если y₁, y₂ 0 , то вычисляются четыре корня по формулами выводятся значения корней.

5. Если условия 3) и 4) не выполняются, то необходимо проверить знак y₁. Если y₁0, то вычисляются два корня по формуле . Если жеy₂0, то вычисляются два корня по формуле 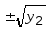. Вычисленные значения корней выводятся.

#include <iostream.h>

#include <math.h>

void main()

{

float a,b,c,d,y1,y2,x1,x2,x3,x4;

cout<<"\n a="; cin>>a;

cout<<"\n b="; cin>>b;

cout<<"\n c="; cin>>c;

d=b*b-4*a*c;

if (d<0) cout<<"resh.net"<<endl;

else

{

y1=(-b+sqrt(d))/2/a;

y2=(-b-sqrt(d))/2/a;

if (y1<0 && y2<0)

cout<<"resh.net"<<endl;

else

if (y1>=0 && y2>=0)

{

x1=sqrt(y1); x2=-x1;

x3=sqrt(y2); x4=-sqrt(y2);

cout<<"x1="<<x1<<endl;

cout<<"x2="<<x2<<endl;

cout<<"x3="<<x3<<endl;

cout<<"x4="<<x4<<endl;

}

else

if (y1>=0)

{

x1=sqrt(y1); x2=-x1;

cout<<"x1="<<x1<<endl;

cout<<"x2="<<x2<<endl;

}

else

{

x1=sqrt(y2); x2=-x1;

cout<<"x1="<<x1<<endl;

cout<<"x2="<<x2<<endl;

}

}

}

Задача 3. Решить кубическое уравнение:

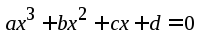(1)

После деления на a уравнение (1) принимает канонический вид:

(2)

где ,,.

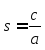В уравнении (2) сделаем замену и получим приведенное уравнение 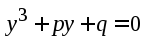(3)

, (3)

Где ,.

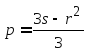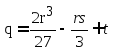Число действительных корней приведенного уравнения (3) зависит от знака дискриминанта :

Количество корней кубического уравнения

Дискриминант	Кол-во действительных корней
D≥0	1
D<0	3

При положительном дискриминанте кубического уравнения (3) действительный корень вычисляется по формулам:

(4)

где .

При отрицательном дискриминанте уравнение (3) имеет 3 действительных корня:

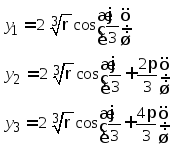, (5)

Где ,.

После расчета корней приведенного уравнения (3) по формулам (4) или (5) необходимо перейти к корням заданного кубического уравнения (1):

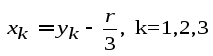
1Текстовые файлы, в которых содержится описание используемых в программе элементов.

2Служат для уточнения внутреннего представления и диапазона значений стандартных типов

3Поток – виртуальный канал связи, создаваемый в программе для передачи данных