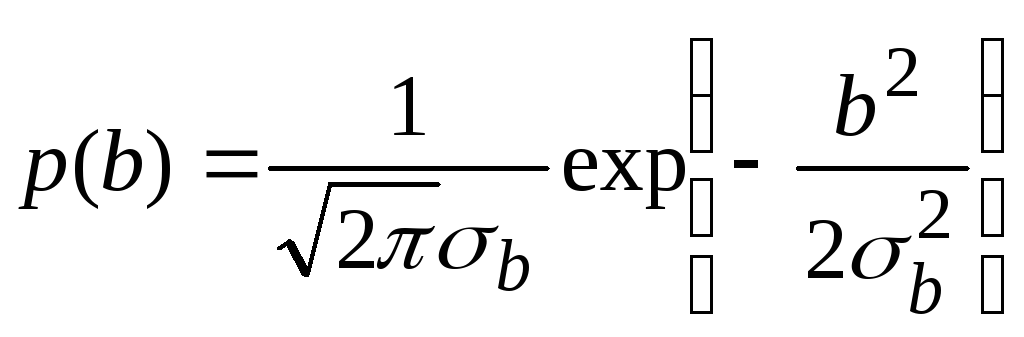3. Расчет параметров кодера и декодера простого кода
Предполагается, что кодирование ведется равномерным кодом, при котором, в отличие от неравномерного кода, более просты в реализации кодер и декодер.
Исходные данные:
объем алфавита источника дискретных сообщений
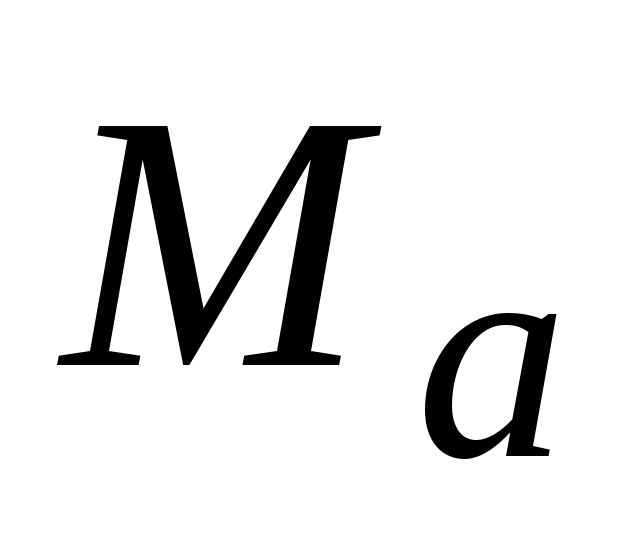 ;
;скорость модуляции на выходе кодера простого кода В;
допустимая вероятность ошибки знака на выходе декодера
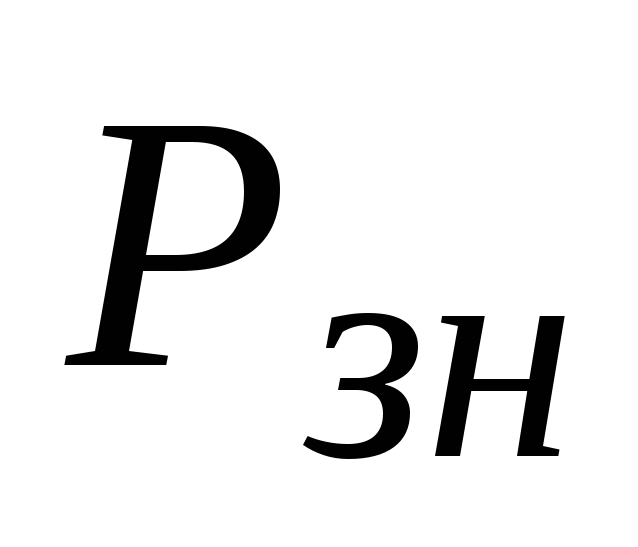 .
.
Требуется определить:
длительность двоичного символа (бита*) на выходе кодера
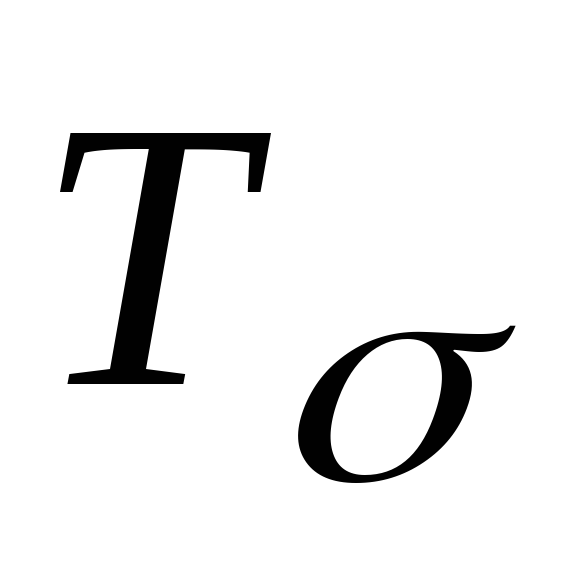 ;
;значность простого кода n;
время передачи одного знака
 ;
;допустимую вероятность ошибки бита на входе декодера
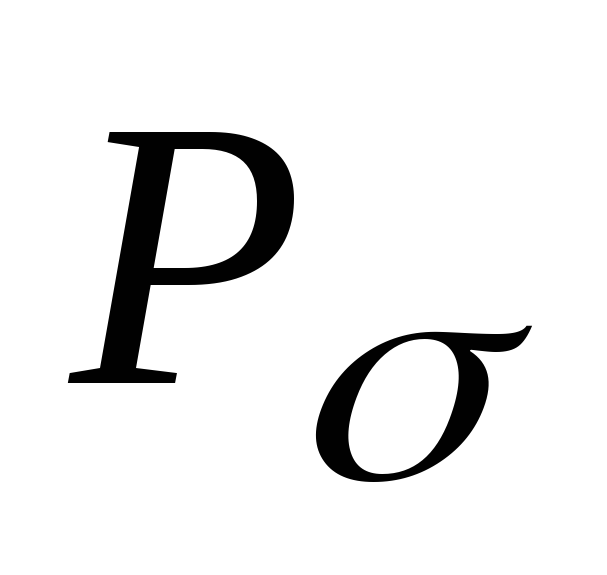 .
.
Длительность двоичного символа на выходе кодера определяется
![]() (3.1)
(3.1)
Значность кода определяется из условия, что число возможных комбинаций не меньше объема алфавита источника
![]() или
или ![]() (3.2)
(3.2)
Поскольку другие требования к коду не предъявляются, то значность кода выбирается как минимальное целое число, при котором выполняются неравенства (3.2).
Время передачи одного знака
![]() (3.3)
(3.3)
Допустимая
вероятность ошибки бита на входе декодера
определяется при условии, что ошибки
символов в канале связи (выход кодера
- вход декодера) независимы:
![]() .
При
.
При![]() .
.
Откуда ![]() (3.4)
(3.4)
РАСЧЕТ ПАРАМЕТРОВ АЦП И ЦАП
Исходные данные для расчетов:
максимальная частота спектра первичного сигнала
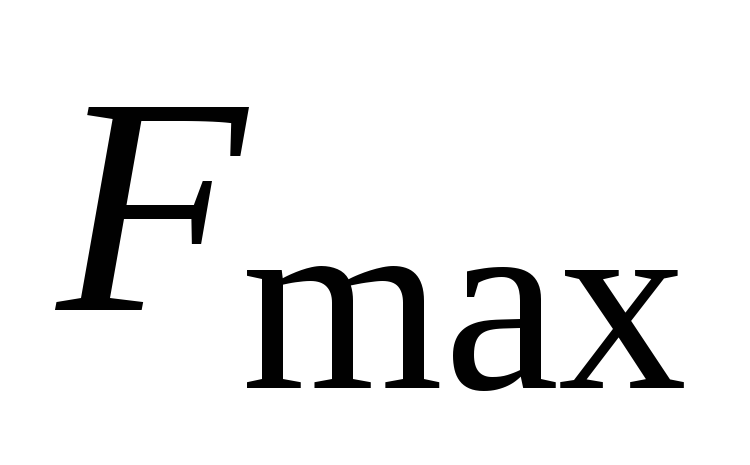 ;
;плотность вероятности мгновенных значений первичного сигнала p(b);
средняя мощность первичного сигнала
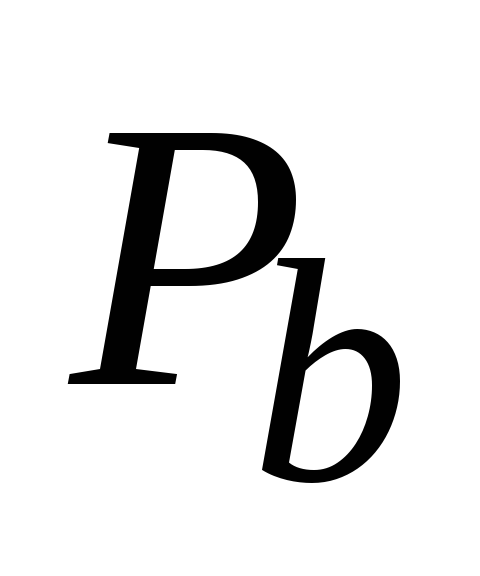 ;
;коэффициент амплитуды первичного сигнала
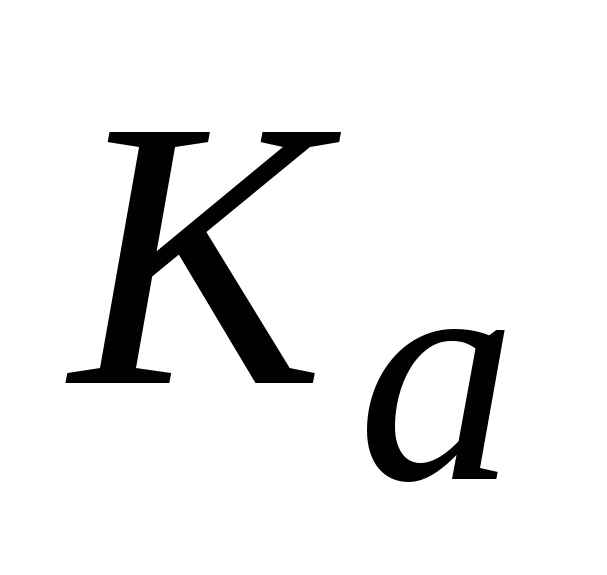 ;
;допустимое отношение сигнал/помеха на входе получателя
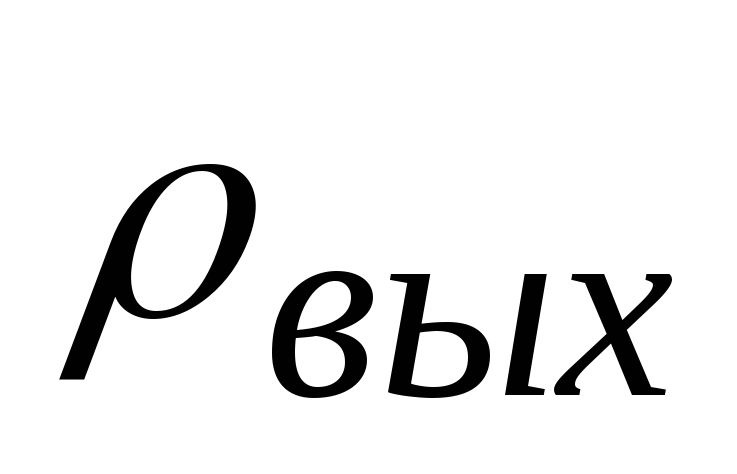 ;
;допустимое значение сигнал/шум квантования
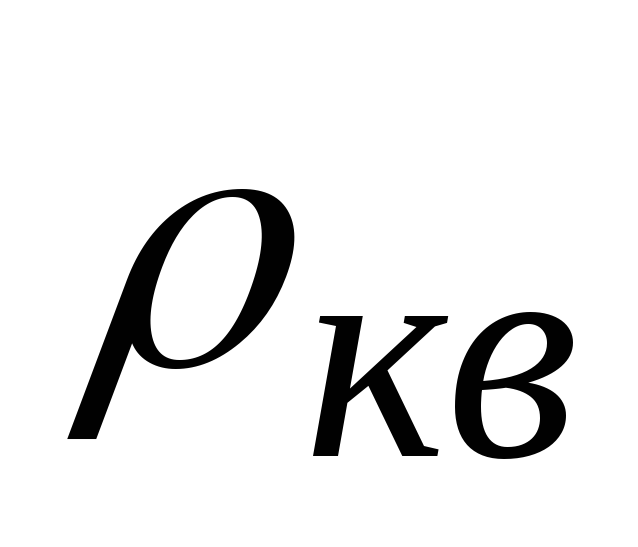 ;
;в АЦП производится равномерное квантование.
Требуется:
составить и описать структурные схемы АЦП и ЦАП;
определить интервал дискретизации
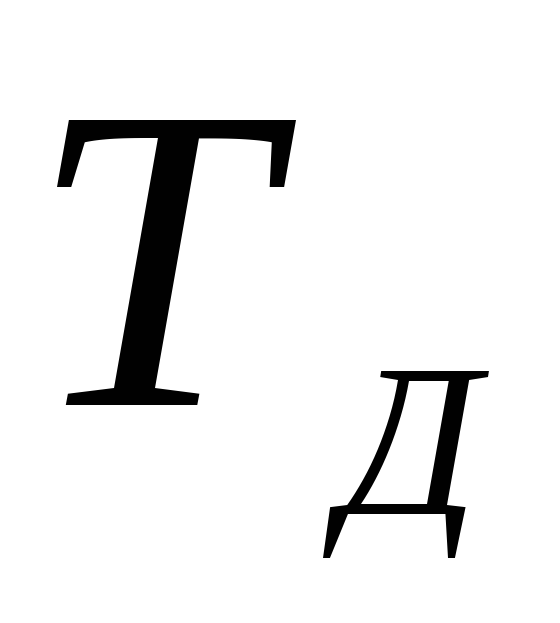 и частоту дискретизации
и частоту дискретизации
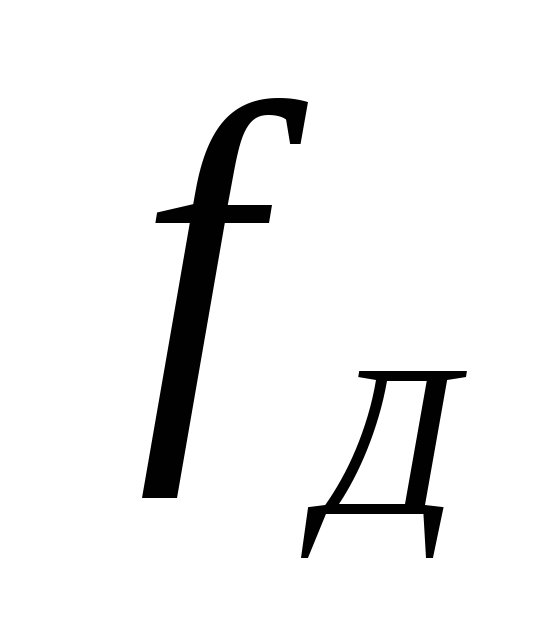 ;
;определить число уровней квантования L и значность двоичного кода n;
рассчитать длительность двоичного символа
 ;
;рассчитать отношение сигнал/шум квантования
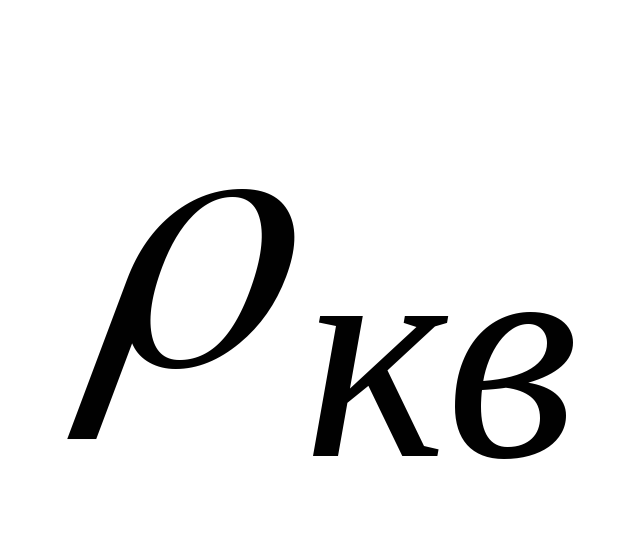 при выбранных параметрах АЦП;
при выбранных параметрах АЦП;рассчитать допустимую вероятность ошибки символа
 в канале связи (на входе ЦАП).
в канале связи (на входе ЦАП).
Структурные схемы АЦП и ЦАП подробно описаны в [1, гл.8; 2, гл.16]. Приведенные там схемы АЦП необходимо дополнить входным ФНЧ, который в реальных системах электросвязи используется для ограничения спектра первичного сигнала. Это связано с тем, что у большинства первичных сигналов спектр является медленно убывающей функцией, и величина
 не есть частота, выше которой спектр
равен нулю, а является граничной частотой
полосы, которую необходимо передать
из условия достижения заданного качества
воспроизведения первичного сигнала
(
не есть частота, выше которой спектр
равен нулю, а является граничной частотой
полосы, которую необходимо передать
из условия достижения заданного качества
воспроизведения первичного сигнала
(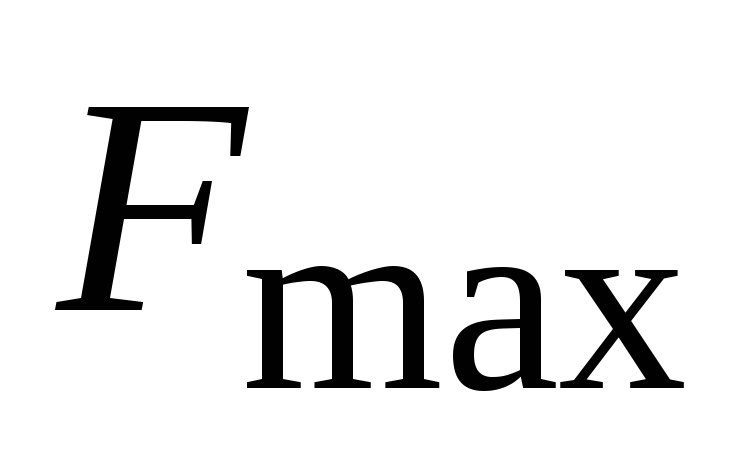 определяется требуемой разборчивостью
речи, четкостью изображения и т.д.).
определяется требуемой разборчивостью
речи, четкостью изображения и т.д.).Интервал дискретизации по времени
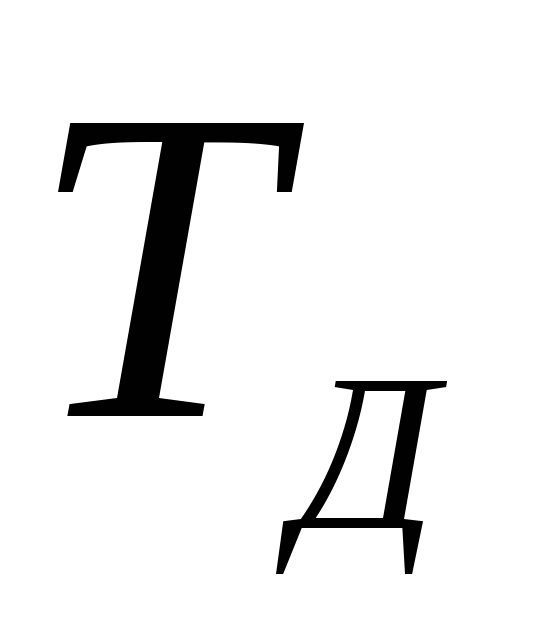 выбирается на основе теоремы Котельникова
[1, разд.2.7;
2, разд. 2.4].
Обратная величина к
выбирается на основе теоремы Котельникова
[1, разд.2.7;
2, разд. 2.4].
Обратная величина к
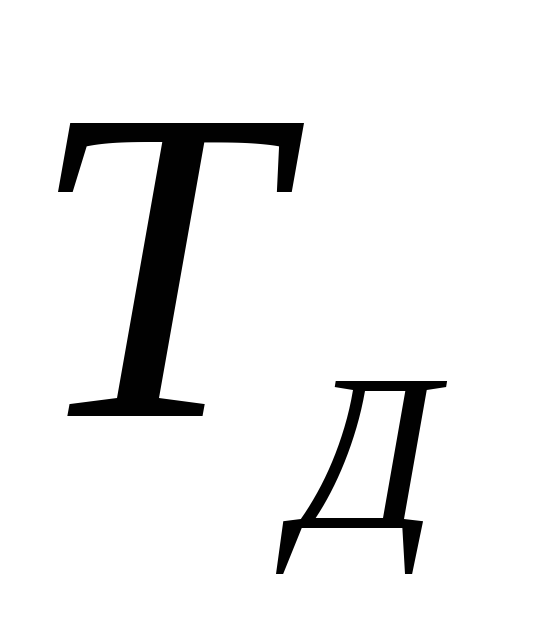 - частота дискретизации
- частота дискретизации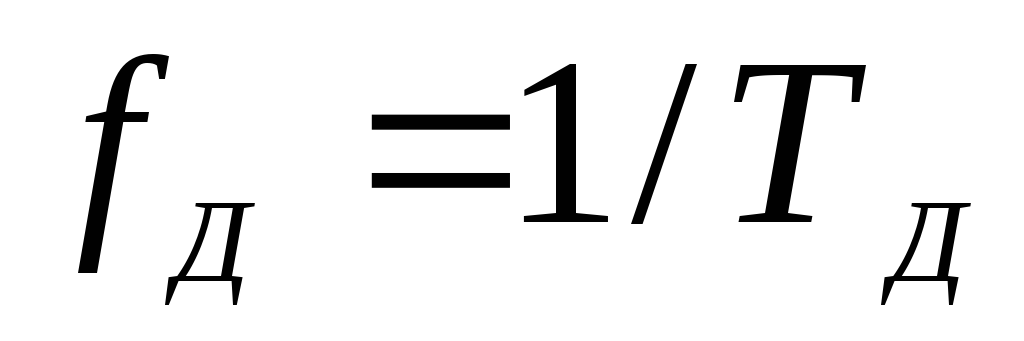 выбирается из условия
выбирается из условия
![]() (4.1)
(4.1)
Увеличение частоты дискретизации позволяет упростить входной фильтр АЦП, ограничивающий спектр первичного сигнала, и выходной (интерполирующий) ФНЧ ЦАП, восстанавливающий непрерывный сигнал по отсчетам. Но увеличение частоты дискретизации приводит к уменьшению длительности двоичных сигналов на выходе АЦП, что требует нежелательного расширения полосы частот канала связи для передачи этих символов. Обычно параметры входного ФНЧ АЦП и выходного ФНЧ ЦАП выбирают одинаковыми.
На
рис. 2 даны:
![]() - спектр отсчетов, представленных узкими
импульсами,
- спектр отсчетов, представленных узкими
импульсами,![]() - спектр непрерывного сигнала
- спектр непрерывного сигнала![]() ,
,![]() - рабочее ослабление ФНЧ. Для того, чтобы
ФНЧ не вносили линейных искажений в
непрерывный сигнал, граничные частоты
полос пропускания ФНЧ должны удовлетворять
условию
- рабочее ослабление ФНЧ. Для того, чтобы
ФНЧ не вносили линейных искажений в
непрерывный сигнал, граничные частоты
полос пропускания ФНЧ должны удовлетворять
условию
![]() (4.2)
(4.2)
Для
того, чтобы исключить наложение спектров
![]() и
и![]() ,
а также обеспечить ослабление
восстанавливающим ФНЧ составляющих
,
а также обеспечить ослабление
восстанавливающим ФНЧ составляющих![]() ,
граничные частоты полос задерживания
ФНЧ должны удовлетворять условию
,
граничные частоты полос задерживания
ФНЧ должны удовлетворять условию
![]() . (4.3)
. (4.3)
Чтобы ФНЧ не были слишком сложными, отношение граничных частот выбирают из условия
![]() . (4.4)
. (4.4)
После
подстановки соотношений (4.2) и (4.3) в (4.4)
можно выбрать частоту
![]() .
.


Так,
например, для речевых сигналов с
![]() =3400
Гц Международным Консультативным
Комитетом по Телеграфии и Телефонии
(МККТТ) рекомендовано значение
=3400
Гц Международным Консультативным
Комитетом по Телеграфии и Телефонии
(МККТТ) рекомендовано значение
![]() =8
кГц.
=8
кГц.
Помехоустойчивость системы передачи непрерывных сообщений определяется величиной
![]() (4.5)
(4.5)
где
![]() -
средняя мощность первичного сигнала;
-
средняя мощность первичного сигнала;
![]() -
средняя мощность помехи на выходе
системы передачи.
-
средняя мощность помехи на выходе
системы передачи.
В системе цифровой передачи методом ИКМ мощность помехи на выходе ЦАП определяется
![]() , (4.6)
, (4.6)
где
![]() - средняя мощность шума квантования;
- средняя мощность шума квантования;
![]() -
средняя мощность шумов ложных импульсов.
-
средняя мощность шумов ложных импульсов.
Если
задано отношение сигнал/шум квантования
![]() ,
то
,
то
![]() . (4.7)
. (4.7)
Если
же
![]() не задано, а задано
не задано, а задано![]() ,
то полагают, что
,
то полагают, что
![]() (4.8)
(4.8)
При проведении расчетов по формулам (4.5) и (4.7) заданные в децибелах отношения сигнал/помеха необходимо представить в разах
![]() . (4.9)
. (4.9)
Мощность
шума квантования выражается через
величину шага квантования
![]() [1, ф-ла (8.8)]
[1, ф-ла (8.8)]
![]() . (4.10)
. (4.10)
Шаг квантования зависит от числа уровней квантования L
![]() (4.11)
(4.11)
Здесь
предполагается, что первичный сигнал
![]() ,
подлежащий преобразованию в цифровой
сигнал, принимает значения от
,
подлежащий преобразованию в цифровой
сигнал, принимает значения от
![]() до
до
![]() и интервал (
и интервал (![]() ,
,![]() )
подлежит квантованию. У сигналов со
средним значением равным нулю
)
подлежит квантованию. У сигналов со
средним значением равным нулю![]() .
Если значение
.
Если значение![]() не задано, то оно определяется с помощью
соотношения
не задано, то оно определяется с помощью
соотношения
![]() (4.12)
(4.12)
где
![]() - коэффициент амплитуды (в [1] обозначается
П и называется пик-фактором). Он
характеризует превышение максимальным
(амплитудным) значением сигнала его
среднеквадратического значения, равного
корню из средней мощности сигнала.
- коэффициент амплитуды (в [1] обозначается
П и называется пик-фактором). Он
характеризует превышение максимальным
(амплитудным) значением сигнала его
среднеквадратического значения, равного
корню из средней мощности сигнала.
На основе соотношений (4.10) и (4.11) минимально возможное число уровней квантования определяется
![]() (4.13)
(4.13)
Значность двоичного кода АЦП
![]() (4.14)
(4.14)
есть целое число. Поэтому число уровней квантования L выбирается как такая целая степень числа 2, при которой
![]() (4.15)
(4.15)
После выбора величины L необходимо рассчитать отношение сигнал/шум квантования [1, ф-ла (8.11)]
![]() (4.16)
(4.16)
Для определения допустимой вероятности ошибки двоичного символа на входе ЦАП
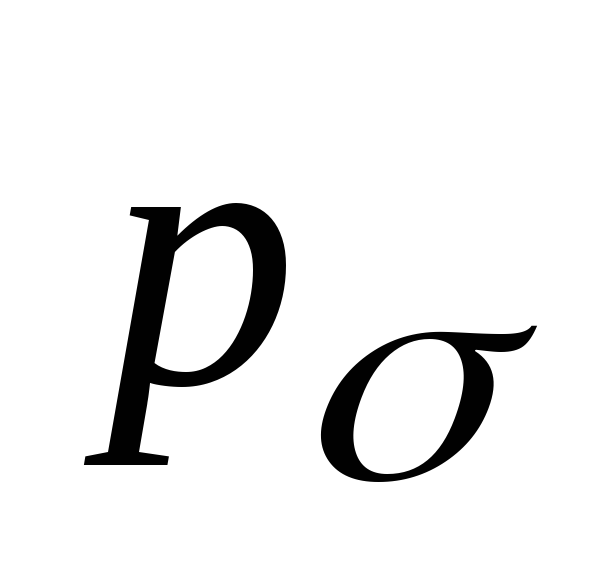 необходимо предварительно определить
допустимую величину мощности шума
ложных импульсов на основе соотношения
(4.6)
необходимо предварительно определить
допустимую величину мощности шума
ложных импульсов на основе соотношения
(4.6)
![]() (4.17)
(4.17)
Здесь
![]() -мощность шума квантования, определяемая
соотношениями (4.10) и (4.11) при выбранном
числе уровней квантованияL.
Далее воспользуемся соотношением [1,
ф-ла (8.14)], связывающим
-мощность шума квантования, определяемая
соотношениями (4.10) и (4.11) при выбранном
числе уровней квантованияL.
Далее воспользуемся соотношением [1,
ф-ла (8.14)], связывающим
![]() и вероятность ошибки бита на входе ЦАП
и вероятность ошибки бита на входе ЦАП
![]()
![]() (4.18)
(4.18)
Величина
шага квантования определяется формулой
(4.11). Соотношение (4.18) позволяет рассчитать
допустимую вероятность ошибки символа
![]() на входе ЦАП.
на входе ЦАП.
Длительность двоичного символа на выходе АЦП определяется
![]() (4.19)
(4.19)
РАСЧЕТ ИНФОРМАЦИОННЫХ ХАРАКТЕРИСТИК ИСТОЧНИКА СООБЩЕНИЙ И ПЕРВИЧНЫХ СИГНАЛОВ
.Расчет информационных характеристик источника непрерывных сообщений
Сообщение
непрерывного источника преобразуется
в первичный аналоговый сигнал
![]() обычно без потери информации, поэтому
расчеты информационных характеристик
источника проводятся для первичного
сигнала
обычно без потери информации, поэтому
расчеты информационных характеристик
источника проводятся для первичного
сигнала
Исходные данные для расчета:
плотность вероятности мгновенных значений первичного сигнала
 ;
;максимальная частота спектра первичного сигнала
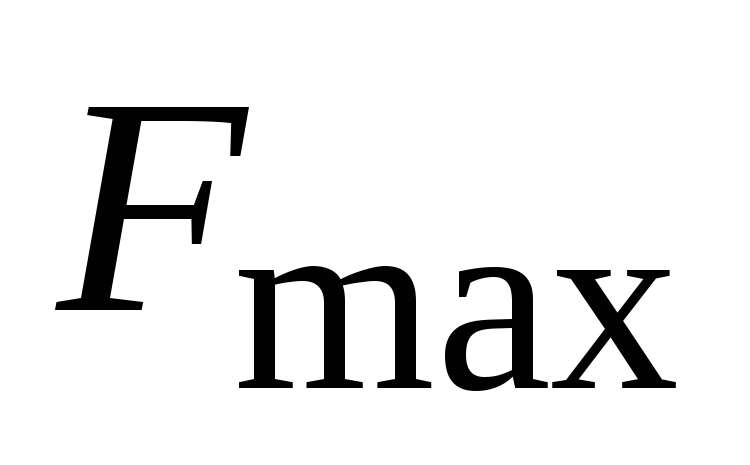 ;
;отношение средней мощности первичного сигнала к средней мощности ошибки воспроизведения на выходе системы передачи
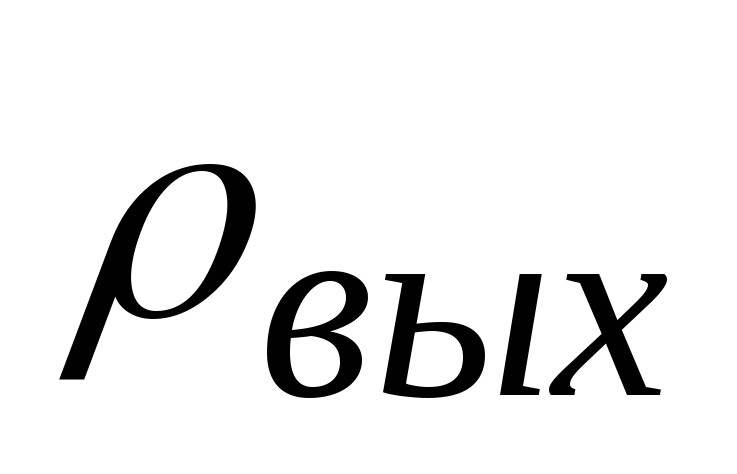 .
.
Подлежат расчету:
эпсилон-энтропия источника
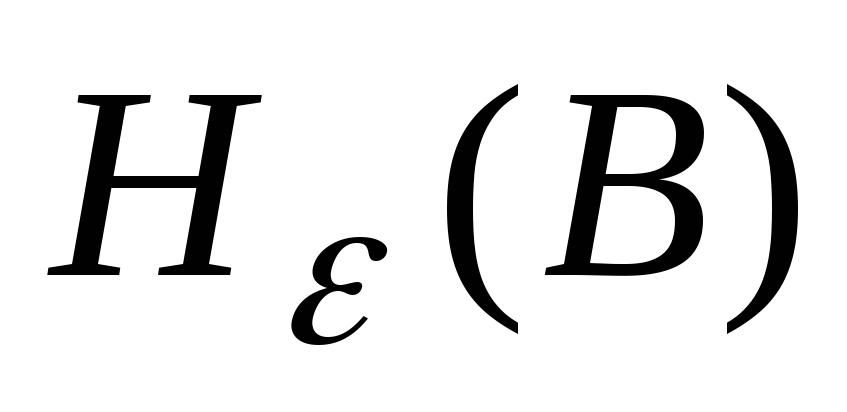 ;
;коэффициент избыточности источника
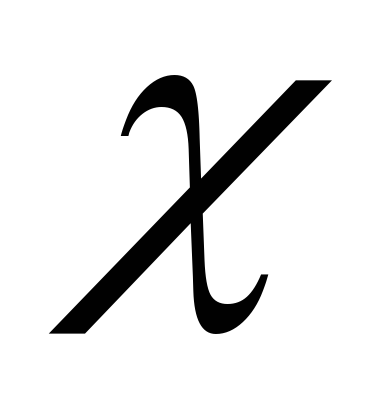 ;
;производительность источника
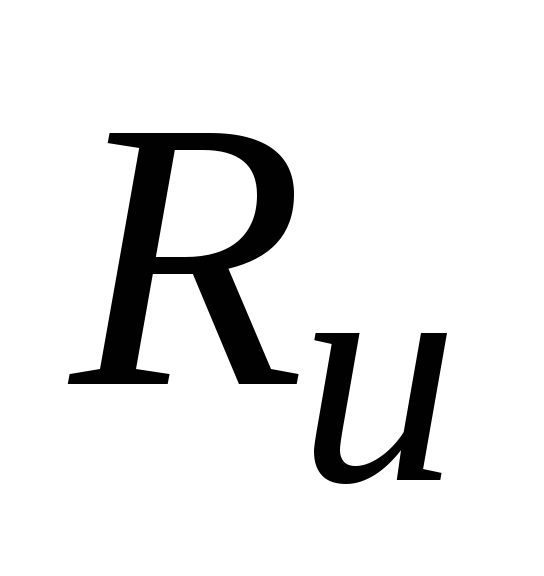 .
.
Сведения
об эпсилон-энтропии и методах ее расчета
даны в [1, разд. 4.7]
- расчетная
формула (4.63). Входящие в формулу (4.63)
дифференциальная энтропия
![]() и условная энтропия
и условная энтропия![]() вычисляются с помощью соотношения
(4.30) в [1] при известных плотностях
вероятности. Дифференциальная энтропия
сигнала зависит от вида распределение
вероятностей
вычисляются с помощью соотношения
(4.30) в [1] при известных плотностях
вероятности. Дифференциальная энтропия
сигнала зависит от вида распределение
вероятностей![]() и дисперсии сигнала
и дисперсии сигнала![]() ,
и соответствующие расчетные формулы
для ее вычислений приведены в табл. 1. У
сигналов со средним значением равным
нулю
,
и соответствующие расчетные формулы
для ее вычислений приведены в табл. 1. У
сигналов со средним значением равным
нулю![]() .
.
При
расчетах полагают, что ошибка
воспроизведения на выходе системы
передачи является гауссовской, и условная
энтропия
![]() вычисляется по формуле (4.34) в [1], в которую
необходимо подставить значение дисперсии
ошибки воспроизведения (мощности помехи
на выходе системы передачи)
вычисляется по формуле (4.34) в [1], в которую
необходимо подставить значение дисперсии
ошибки воспроизведения (мощности помехи
на выходе системы передачи)![]() .
Значение
.
Значение![]() определяется по заданному отношению
сигнал/помеха
определяется по заданному отношению
сигнал/помеха![]() и средней мощности сигнала
и средней мощности сигнала![]() по формуле (4.5).
по формуле (4.5).
Таблица 1. Дифференциальная энтропия для некоторых законов распределения случайных величин
|
Распределение вероятности |
Дифференциальная энтропия , бит/отсчет |
|
Нормальное распределение (рис. 3а)
|
|
|
Двустороннее экспоненциальное распределение (рис. 3б)
|
|
|
Равномерное распределение (рис. 3в)
|
|
Д о
вычислений заданное в децибелах отношение
необходимо представить в разах - формула
(4.9).
о
вычислений заданное в децибелах отношение
необходимо представить в разах - формула
(4.9).
Коэффициент избыточности источника
 вычисляется по формуле (4.10) из [1]. В эту
формулу подставляются вычисленное
значение эпсилон-энтропии
вычисляется по формуле (4.10) из [1]. В эту
формулу подставляются вычисленное
значение эпсилон-энтропии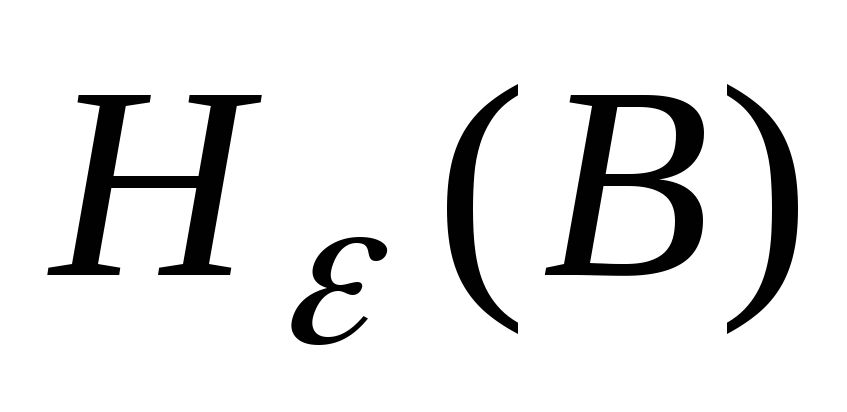 и максимально возможное значение
и максимально возможное значение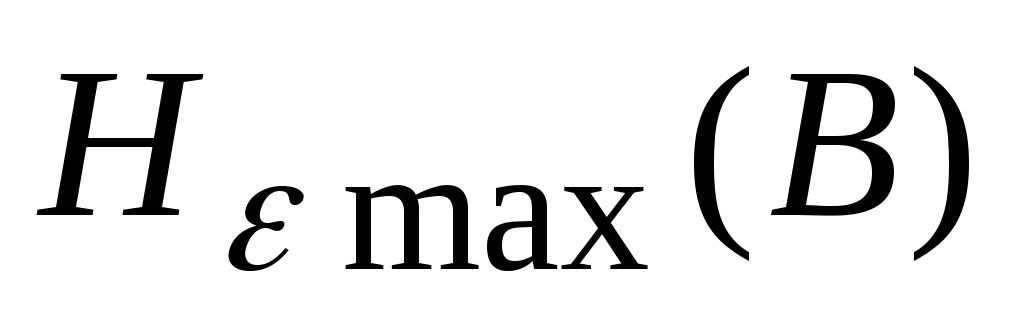 ,
достигаемое при нормальном распределении
вероятности сигнала
,
достигаемое при нормальном распределении
вероятности сигнала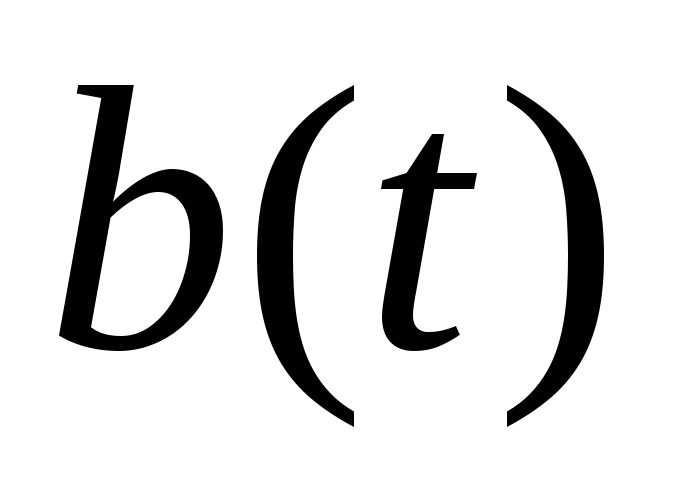 и той же дисперсии сигнала
и той же дисперсии сигнала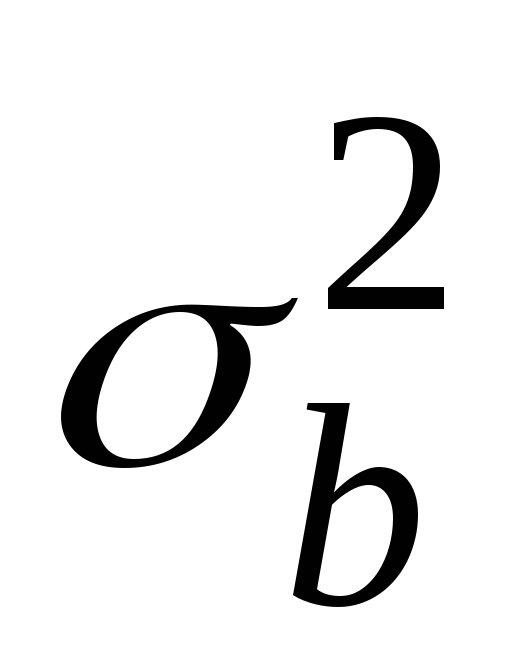 .
.Производительность источника
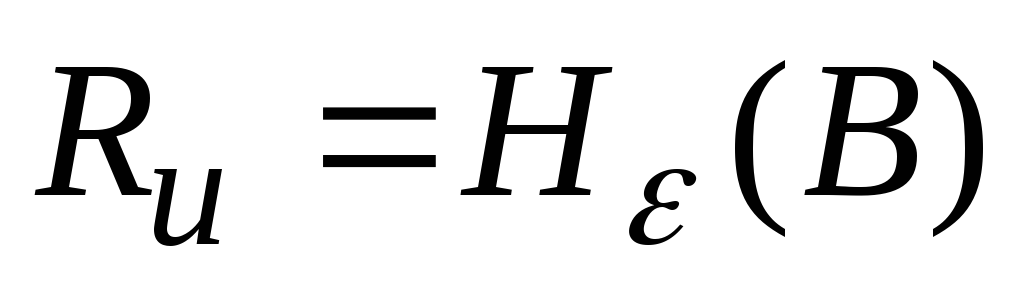 ,
которую называют эпсилон-производительностью,
вычисляют в предположении, что отсчеты
следуют через интервал Котельникова
- формула (4.67) из [1]. В этой формуле
,
которую называют эпсилон-производительностью,
вычисляют в предположении, что отсчеты
следуют через интервал Котельникова
- формула (4.67) из [1]. В этой формуле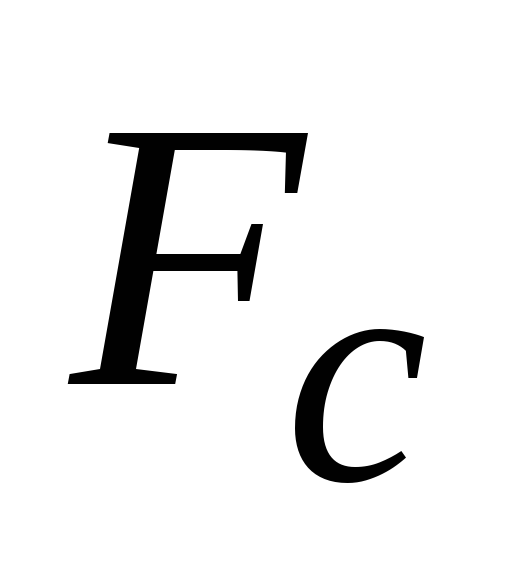 - максимальная частота спектра первичного
сигнала
- максимальная частота спектра первичного
сигнала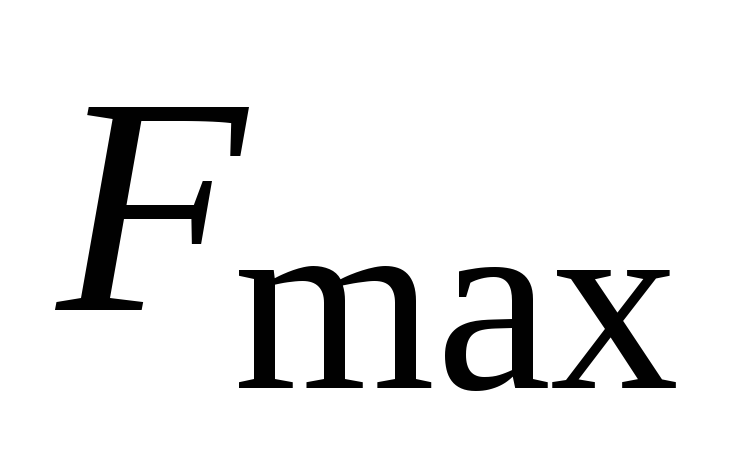 .
Требования к пропускной способности
непрерывного канала связи формулируются
на основе теоремы кодирования для
канала с помехами [1, разд.4.6].
.
Требования к пропускной способности
непрерывного канала связи формулируются
на основе теоремы кодирования для
канала с помехами [1, разд.4.6].
Расчет информационных характеристик источника дискретных сообщений
Исходные данные для расчета:
объем алфавита источника
 ;
;вероятности знаков
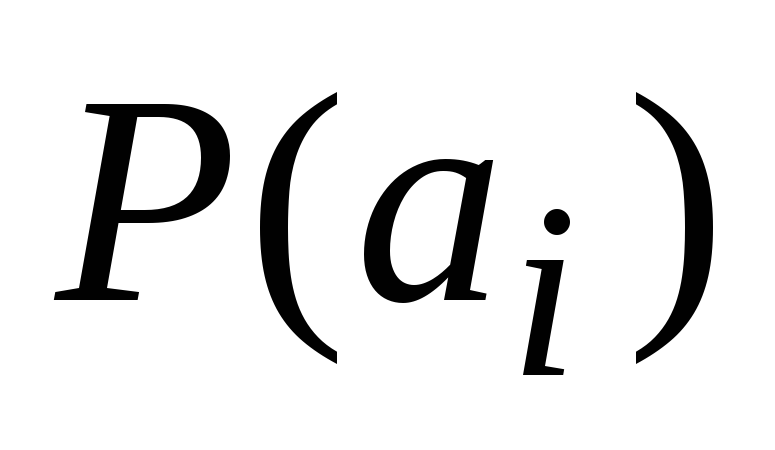 ,
образующих алфавит источника
(предполагается, что знаки в сообщениях
независимы);
,
образующих алфавит источника
(предполагается, что знаки в сообщениях
независимы);время передачи одного знака
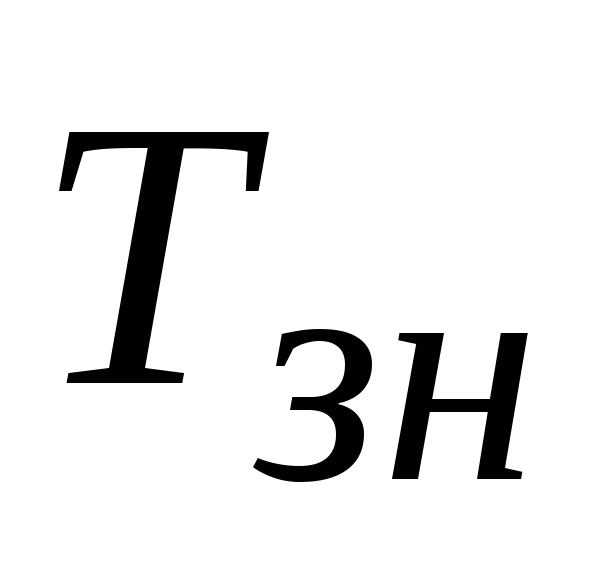 .
.
Подлежат расчету:
энтропия источника
 ;
;коэффициент избыточности источника
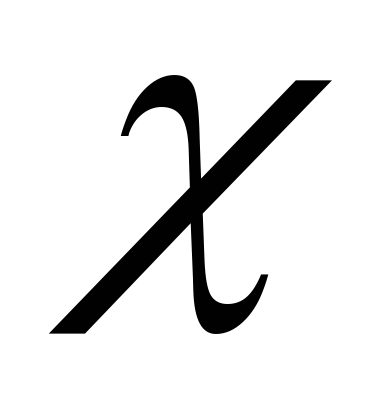 ;
;производительность источника
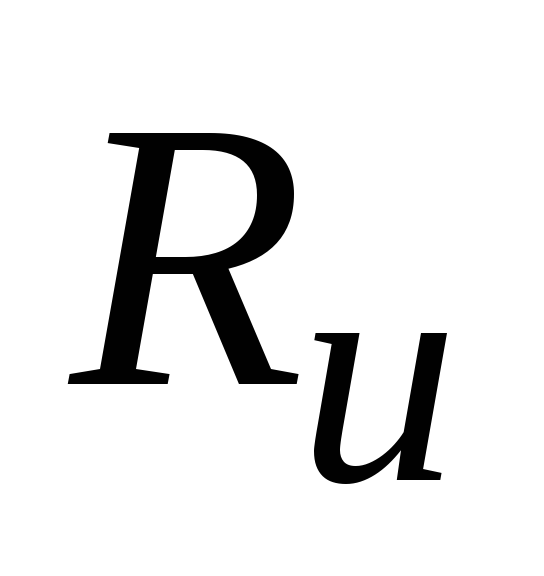 .
.
Расчеты информационных характеристик можно выполнить на основе материала, изложенного в разд. 4.1 учебника [1] . Необходимые для расчетов вероятности букв в украинском, русском и английском текстах приведены в табл. 2, 3 и 4. Расчеты энтропии источника следует выполнять на ЭВМ либо программируемом калькуляторе.
Таблица 2. Распределение вероятностей букв в украинских текстах
|
Буква |
Вероятность |
Буква |
Вероятность |
Буква |
Вероятность |
Буква |
Вероятность |
|
Пробел |
0.122 |
Р |
0.040 |
З |
0.018 |
Ж |
0.007 |
|
О |
0.090 |
С |
0.034 |
И |
0.017 |
Ц |
0.006 |
|
А |
0.074 |
Л |
0.034 |
Б |
0.016 |
Ю |
0.006 |
|
И |
0.059 |
К |
0.034 |
Я |
0.015 |
Ї |
0.006 |
|
І |
0.055 |
У |
0.032 |
Г |
0.013 |
Е |
0.003 |
|
Н |
0.053 |
Д |
0.026 |
Ч |
0.012 |
Ф |
0.002 |
|
В |
0.047 |
П |
0.026 |
Ш |
0.010 |
|
|
|
Т |
0.044 |
М |
0.023 |
Х |
0.008 |
|
|
|
Е |
0.041 |
Ь |
0.021 |
Щ |
0.008 |
|
|
Таблица 3. Распределение вероятностей букв в русских текстах
-
Буква
Вероят
ность
Буква
Вероят
ность
Буква
Вероят
ность
Буква
Вероятность
Пробел
0.175
Р
0.040
Я
0.018
Х
0.009
О
0.089
В
0.038
Ы
0.016
Ж
0.007
Е,Ё
0.072
Л
0.035
З
0.016
Ю
0.006
А
0.062
К
0.028
Ь,Ъ
0.014
Ш
0.006
И
0.062
М
0.026
Б
0.014
Ц
0.004
Т
0.053
Д
0.025
Г
0.013
Щ
0.003
Н
0.053
П
0.023
Ч
0.012
Э
0.003
С
0.045
У
0.021
Й
0.010
Ф
0.002
Таблица 4. Распределение вероятностей букв в английских текстах
-
Буква
Вероят
ность
Буква
Вероят
ность
Буква
Вероят
ность
Буква
Вероятность
Пробел
0.198
R
0.054
U
0.022
V
0.008
E
0.105
S
0.052
M
0.021
K
0.003
T
0.072
H
0.047
P
0.017
X
0.002
O
0.065
D
0.035
Y
0.012
J
0.001
A
0.063
L
0.029
W
0.012
Q
0.001
N
0.059
C
0.023
G
0.011
Z
0.001
I
0.055
F
0.022
B
0.010
Производительность
источника
![]() легко определить, зная энтропию и время
передачи одного знака [1, ф-ла (4.11)].
легко определить, зная энтропию и время
передачи одного знака [1, ф-ла (4.11)].
Требования к пропускной способности дискретного канала связи формулируются на основе теоремы кодирования для канала с помехами [1, разд. 4.6].