2. Расчет ячеечного реактора и теплообменника

2.1 Постановка задачи для реактора

Химические реакции проводятся в основном в аппаратах, называемых химическими реакторами. В зависимости от теплового режима, в котором протекает реакция, ее можно проводить либо в трубчатых реакторах (неизотермические режимы), либо в аппаратах с мешалкой (реакторы идеального смешения чаще всего применяются для изотермических процессов). Многие химические процессы с целью повышения степени превращения проводят в нескольких последовательно соединенных реакторах идеального смешения.

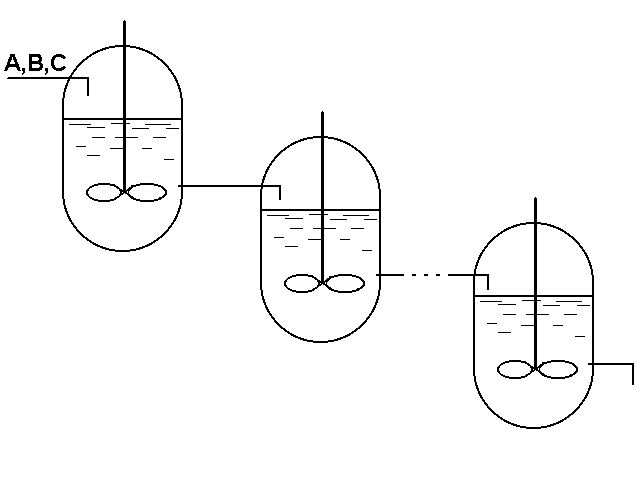
Рисунок 2.1 – Схема ячеечного реактора.

Структура потоков в аппаратах подобного типа близка к ячеечной модели, если предположить, что взаимодействия между реагирующими веществами при перетекании их из реактора в реактор не происходит. Таким образом, концентрация С_i,j любого компонента в смеси, поступающей в последующий реактор (рис.3.1)равна концентрации его в предыдущем реакторе C_i-1,j.

2.2 Вывод математического описания для реактора

Математическое описание для нестационарных условий проведения процесса имеет вид:

(1)

где R_i,j – суммарная скорость по j-му компоненту в i-м реакторе;n – количество реакторов в каскаде;m – количество реагирующих веществ.

Допустим, в каскаде реакторов в изотермических условиях протекает химическая реакция:

К₃ К₁

C A B

К₂

Необходимо для установившегося режима определить количество реакторов в каскаде, при котором выход продукта В был бы максимальным, а выход побочного продукта С возможно меньшим. Для данного химического процесса в стационарных условиях работы математическое описание будет иметь вид:

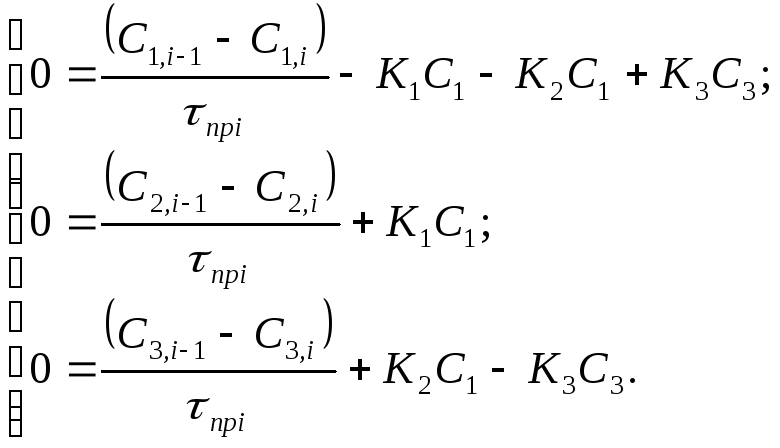(2)

Преобразуем систему (2), разделив дроби почленно:

(3)

Таким образом может быть вычислена концентрация реагирующих веществ вначале в первом реакторе, а затем во втором и т.д. Сравнивая концентрацию компонента В в очередном реакторе с концентрацией в предыдущем можно найти такое количество реакторов в каскаде, при котором выход продукта В будет наибольшим. Варьируя величиной констант K₁ и K₂, а также временем пребывания (τ_{пр i}) в реакторах каскада, можно провести исследования работы ячеечной модели и найти наилучший вариант работы.

Систему линейных уравнений (3) можно решить методом Гаусса, но для этого надо привести её к виду:

A · X = B, (4)

где А – двумерный массив коэффициентов при неизвестных;

Х – одномерный массив текущих концентраций;

В – одномерный массив свободных членов.

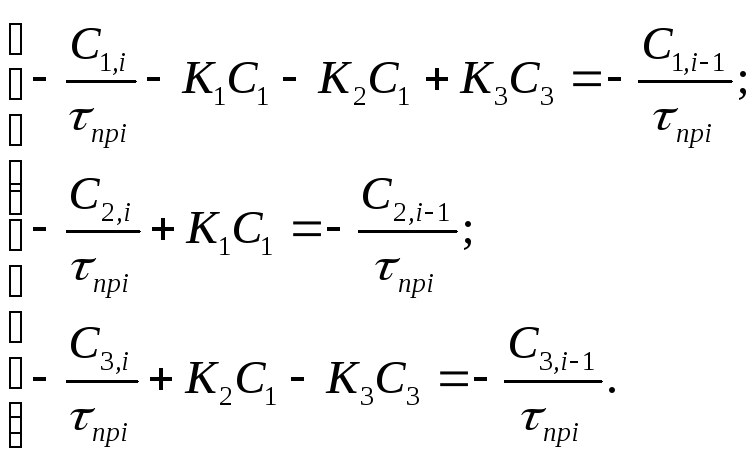(5)

Сгруппируем слагаемые, содержащие одинаковые концентрации и получим:

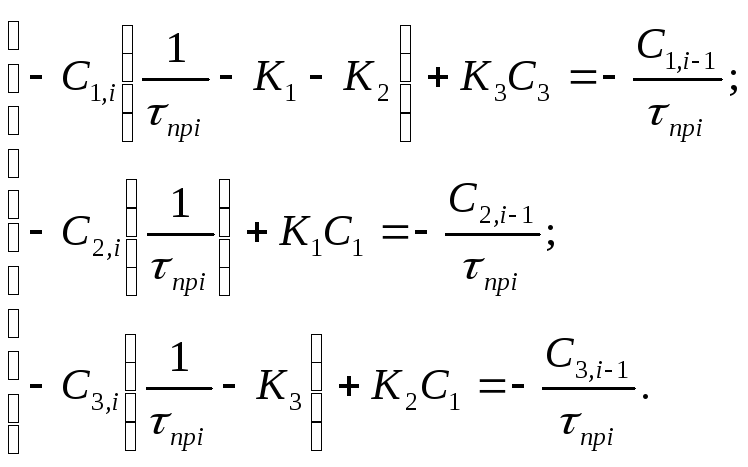(6)

Представим полученную систему линейных уравнений в виде табл. 2.1.

Таблица 2.1 – Таблица массивов

Массив А			Массив В	Массив Х
Ca	Cb	Cc
	0	K3		C1
K1		0		C2
K2	0			C3

2.3 Идентификация переменных для реактора

В связи с некоторыми особенностями представления переменных, векторов и массивов на языке LabView, невозможностью использования греческих букв и т.д. мы вынуждены прибегать к использованию специфических представлений переменных, а, следовательно, и таблицы идентификации.

Таблица 2.2 – Идентификация переменных

№ п/п	Перемен. в прогр.	Переменная в мат.опис.	Смысл и размерность переменной	Значение
1 2 3 4 5 6 7 8 9 10	Сi,1 Сi,2 Сi,3 Tau К1 К2 K3 Q I j	Са Сb Сc τ К1 К2 K3 Q I j	Концентрация компонента А в i-той яч.,% Концентрация компонента Bвi-той яч.,% Концентрация компонента Cвi-той яч.,% Время пребывания в i-той яч.,с Константа скорости,1/с Константа скорости,1/с Константа скорости,1/с Таблица результатов Порядковый номер строки Порядковый номер реактора	при i=0 Са=100 при i=0 Сb=0 при i=0 Сc=0 1 0.4 0.1 0.2

2.4 Постановка задачи для теплообменника

С целью использования вторичных энергоресурсов на химических заводах находит широкое применение теплообменная аппаратура. В теплообменниках различной конструкции происходит передача тепла от горячего технологического вещества к холодному.

Целью работы является составление математической модели аппарата и её дальнейшее исследование с получением зависимости распределения температуры по длине при различных расходах теплоносителей и вида их движения (прямоток и противоток).

2.5 Вывод математического описания для теплообменника

Для теплообменника типа „труба в трубе” (рис. 3.3), структура потока близка к идеальному вытеснению (для обоих теплоносителей). Тогда математическое описание можно записать в виде:

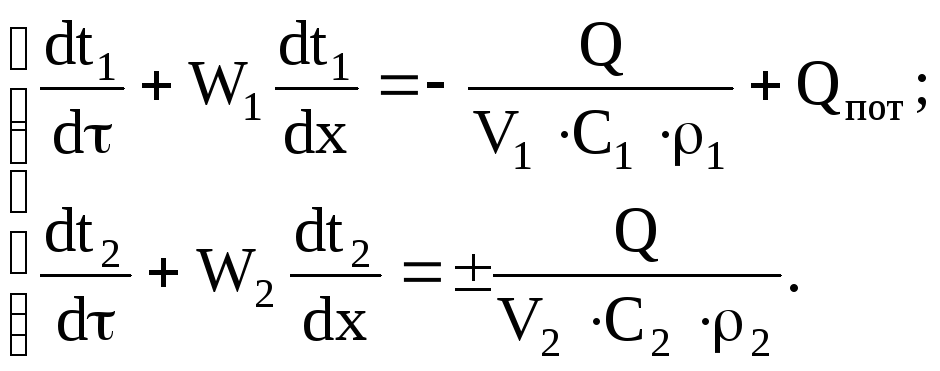(8)

где W₁,W₂ – линейные скорости движения горячего и холодного теплоносителей, м/c (векторные величины, знак которых зависит от направления движения);

Q – количество переданного тепла, Вт;

V₁,V₂ – объемы горячего и холодного теплоносителей в теплообменнике, м³;

C₁,C₂ – теплоемкости теплоносителей, Дж/кг·К;

ρ₂, ρ₂ – плотности теплоносителей, кг/м³.

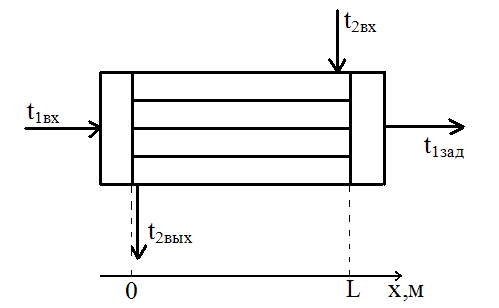
Рисунок 2.3 – Схема теплообменника.

Если направление движения противоположно направлению оси X, то знак W – отрицательный.

Без учета потерь в установившемся режиме, уравнения принимают следующий вид:

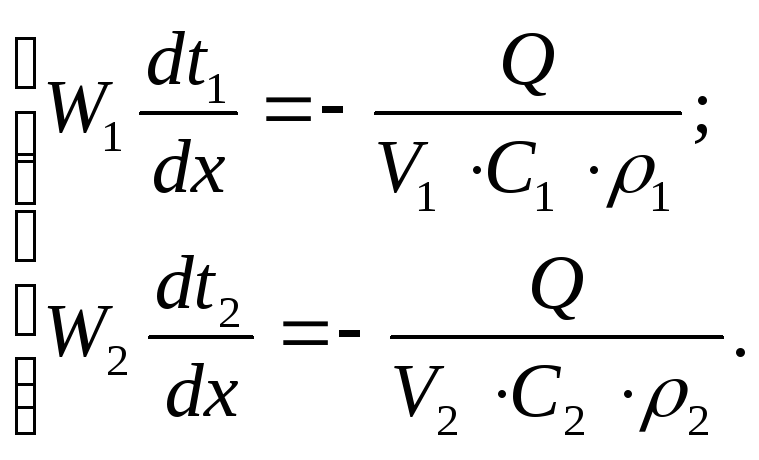(9)

Введя известные соотношения:

Q=K·F·(t₁ – t₂);

F= π·d·l;

W=Vc/S;

V=S·l,

F=P*l

где S – площадь сечение для прохода теплоносителя, м²;

l – длина теплообменника, м;

К – коэффициент теплопередачи,Вт/(м²·К);

Р – смоченный периметр, м;

Vc – объемный расход теплоносителя, м³/c;

d – диаметр внутренней трубы, м,

получим математическое описание теплообменника (для противотока):

(10)

Решая эту систему дифференциальных уравнений при соответствующих условиях однозначности, можно получить распределение температур теплоносителей по длине теплообменника. Для случая прямотока во втором уравнении следует в правой части поставить знак плюс.