2.2 Алгоритмы подавления шума

2.2.1 Фильтр свертка с маской и медианный фильтр

Свертка – это операция вычисления нового значения выбранного пикселя, учитывающая значения окружающих его пикселей. Для вычисления значения используется матрица, называемая ядром свертки. Обычно ядро свертки является квадратной матрицей n*n, где n – нечетное, однако ничто не мешает сделать матрицу прямоугольной. Во время вычисления нового значения выбранного пикселя ядро свертки как бы «прикладывается» своим центром (именно тут важна нечетность размера матрицы) к данному пикселю. Окружающие пиксели так же накрываются ядром. Далее высчитывается сумма, где слагаемыми являются произведения значений пикселей на значения ячейки ядра, накрывшей данный пиксель. Сумма делится на сумму всех элементов ядра свертки. Полученное значение как раз и является новым значением выбранного пикселя. Если применить свертку к каждому пикселю изображения, то в результате получится некий эффект, зависящий от выбранного ядра свертки.

Медианный фильтр – один из видов цифровых фильтров, широко используемый вцифровой обработке сигналовиизображенийдля уменьшения уровняшума. Медианный фильтр являетсянелинейнымКИХ-фильтром.

Значения отсчётов внутри окна фильтра сортируются в порядке возрастания (убывания); и значение, находящееся в середине упорядоченного списка, поступает на выход фильтра. В случае четного числа отсчетов в окне выходное значение фильтра равно среднему значению двух отсчетов в середине упорядоченного списка. Окно перемещается вдоль фильтруемого сигнала и вычисления повторяются.

Медианная фильтрация – эффективная процедура обработки сигналов, подверженных воздействию импульсных помех.

Последовательный алгоритм данного метода:

• фильтрация проводится построчно – для первого элемента строки заполняется массив окрестности (с учетом того, что искусственно добавляются три значения-соседи слева), этот массив сортируется быстрой сортировкой, затем среднее значение записывается в выходную матрицу;

• для каждого следующего элемента строки массив окрестности не заполняется заново – в него лишь добавляются новые три элемента, замещая старые три. Для того, чтобы это было возможно сделать за один проход (по массиву окрестности и новым трем элементам) введен специальный массив с «количеством жизней» элемента. Жизней может быть 1, 2 и 3;

• добавляемые 3 элемента предварительно сортируются и добавление производится слиянием: во время него элементы с 1й жизнью затираются, элементы, имевшие 2 и 3 жизни получают 1 и 2 соответственно, а добавляемые элементы становятся обладателями 3х жизней;

• средний элемент записывается в выходной массив.

Обработка последнего элемента производится повторением итерации предпоследнего шага.

На практике данный метод по сравнению с полной выборкой окрестности и ее сортировкой показывает превосходство по скорости в 3 раза.

2.2.2 Метод k-ближайших соседей

Здесь идея состоит в том, что вокруг распознаваемого объекта строится ячейка объёма. При этом неизвестный объект относится к тому образу, число обучающих представителей которого в построенной ячейке оказалось большинство. Если использовать статистическую терминологию, то число объектов образа, попавших в данную ячейку, характеризует оценку усреднённой по объёмуплотности вероятности.

Для оценки усреднённых нужно решить вопрос о соотношении между объёмомячейки и количеством попавших в эту ячейку объектов того или иного класса (образа). Вполне разумно считать, что чем меньше, тем более тонко будет охарактеризована. Но при этом тем меньше объектов попадёт в интересующую нас ячейку, а следовательно, тем меньше достоверность оценки. При чрезмерном увеличениивозрастает достоверность оценки, но теряются тонкости её описания из-за усреднения по слишком большому объёму, что может привести к негативным последствиям (увеличению вероятности ошибок распознавания). При небольшом объёме обучающей выборкицелесообразно брать предельно большим, но обеспечить при этом, чтобы внутри ячейки плотностимало изменялись. Тогда их усреднение по большому объёму не очень опасно. Таким образом, вполне может случиться, что объём ячейки, уместный для одного значения, может совершенно не годиться для других случаев.

Предлагается следующий порядок действий (пока что принадлежность объекта тому или иному образу учитывать не будем).

Для того чтобы оценить на основании обучающей выборки, содержащейобъектов, центрируем ячейку вокруги увеличиваем её объём до тех пор, пока она не вместитобъектов, гдеесть некоторая функция от. Этиобъектов будут ближайшими соседями. Вероятностьпопадания векторав областьопределяется выражением

,

(2.1)

Это сглаженный (усреднённый) вариант плотности распределения . Если взять выборку изобъектов (простым случайным выбором из генеральной совокупности), тоиз них окажется внутри области. Вероятность попаданияизобъектов вописывается биномиальным законом, имеющим резко выраженный максимум около среднего значения. При этомявляется неплохой оценкой для.

Если теперь допустить, что настолько мала, чтовнутри неё меняется незначительно, то

,

(2.2)

где – объём области;

–точка внутри .

Тогда

,

(2.3)

Но

,

(2.4)

Следовательно:

(2.5)

Итак, оценкой плотностиявляется величина

(2.6)

Без доказательства приведём утверждение, что условия

, ,	(2.7) (2.8)

являются необходимыми и достаточными для сходимости кпо вероятности во всех точках, где плотностьнепрерывна.

Этому условию удовлетворяет, например, .

Теперь будем учитывать принадлежность объектов к тому или иному образу и попытаемся оценить апостериорные вероятности образов

Предположим, что мы размещаем ячейку объёма вокруги захватываем выборку с количеством объектов,из которых принадлежат образу. Тогда в соответствии с формулойоценкой совместной вероятностибудет величина

, а		(2.9)
.	(2.10)

Таким образом, апостериорная вероятность оценивается как доля выборки в ячейке, относящаяся к. Чтобы свести уровень ошибки к минимуму, нужно объект с координатамиотнести к классу (образу), количество объектов обучающей выборки которого в ячейке максимально. Притакое правило является байесовским, то есть обеспечивает теоретический минимум вероятности ошибок.
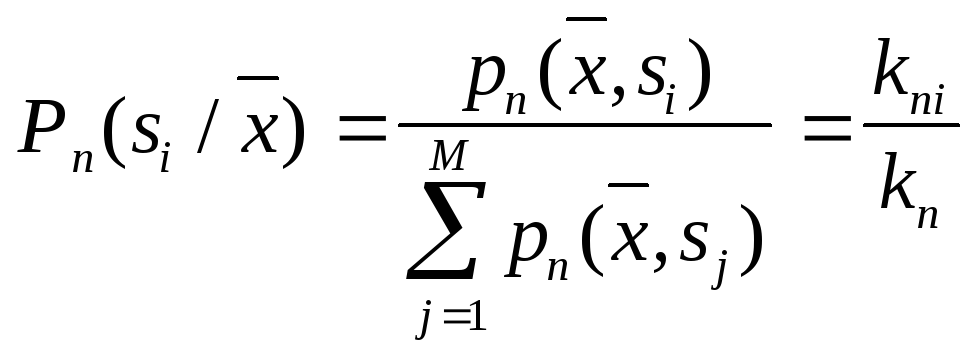