Примитивная рекурсивность логических функций

Примитивно-рекурсивными могут быть не только арифметические функции, но и « арифметизованные » логические функции, отношения, предикаты, операторы.

« Арифметизованная » логическая функция – это такая числовая арифметическая функция, которая на множестве {0,1} ведет себя также, как логическая.

Операции 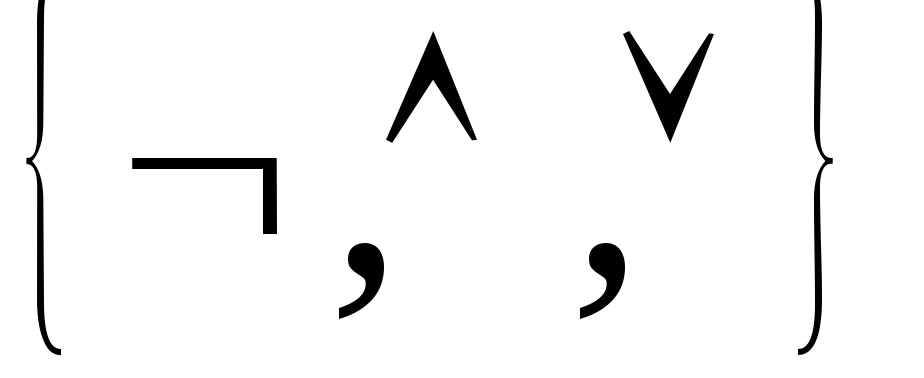на множестве {0,1} примитивно-рекурсивны.

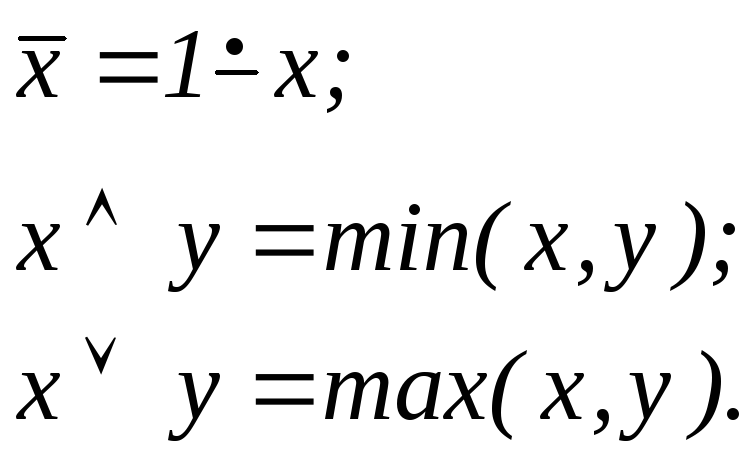
Функции 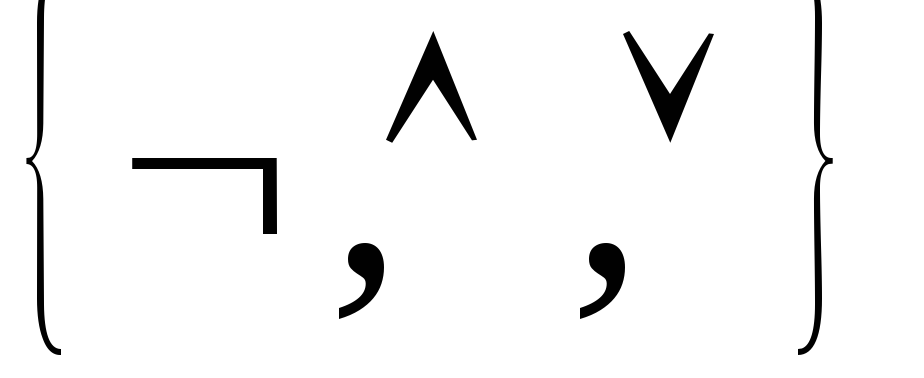на множестве {0,1} образуют базис, следовательно, все остальные арифметизованные логические функции могут быть представлены в виде суперпозиции этих трёх функций, а, следовательно, по определению примитивной рекурсивности они примитивно-рекурсивны.

Отношение называетсяпримитивно-рекурсивным, если примитивно-рекурсивна его характеристическая функция :

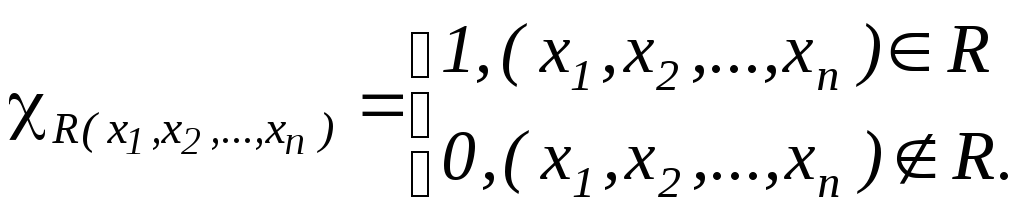
Пример 11. Отношение – примитивно-рекурсивно.

Действительно, .

Отношение примитивно-рекурсивно.

Действительно, .

Отношение примитивно-рекурсивно.

Действительно,

Предикат – функция, определяющая обладают ли ее аргументы свойством или нет и возвращает значение: , {“false”,“true”}, {“ложь”, ”истина”}.

Предикат называетсяпримитивно-рекурсивным, если примитивно-рекурсивна его характеристическая функция:

.

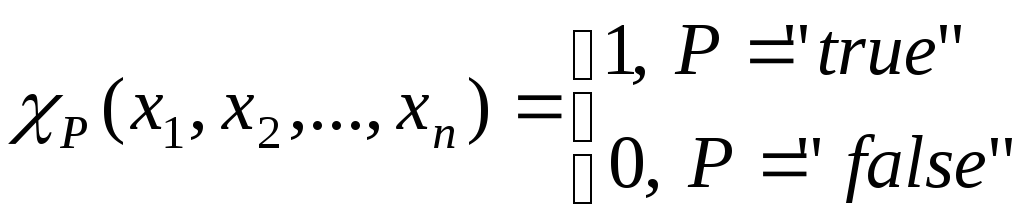Оператор называется примитивно-рекурсивным, если он сохраняет примитивную рекурсивность функций, т.е. если результат его применения к примитивно-рекурсивным функциям дает снова примитивно-рекурсивную функцию.

Пример 12. Примитивная рекурсивность оператора условного перехода

.

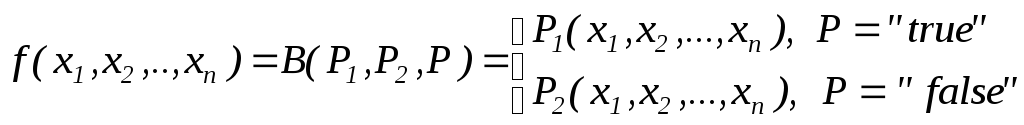
где и– примитивно-рекурсивные функции;P – примитивно-рекурсивный предикат. Примитивная рекурсивность функции (оператораB) следует из равенства:

Частично-рекурсивные функции

Большинство арифметических и логических функций являются примитивно-рекурсивными. Однако класс примитивно-рекурсивных функций не охватывает всех вычислимых в интуитивном смысле функций. Для построения остальных функций используется так называемый оператор минимизации ( -оператор, оператор наименьшего корня).

Оператор минимизации определяет новую арифметическую функцию отn переменных с помощью ранее построенной арифметической функции отn+1 переменных. Пусть существует некоторый механизм вычисления функции , причем значение функциинеопределенно, если этот механизм работает бесконечно, не выдавая никакого определенного значения.

Зафиксируем набор значений аргументов и рассмотрим уравнение относительноy: ; чтобы найти решение этого уравнения, натуральное, будем вычислять последовательность значений:

для ..

Наименьшее целое неотрицательное значение , удовлетворяющее этому уравнению:обозначим:

.

Говорят, что функция получена из функцииоперацией минимизации, если:

Оператор минимизации работает бесконечно в одном из следующих случаев:

1) значение не определено;

2) значение дляопределены, но не равны нулю, а значение– не определено;

3) значение определены для всех, но не равны нулю.

Пример 13. Процесс вычисления функции с помощью оператора минимизации:

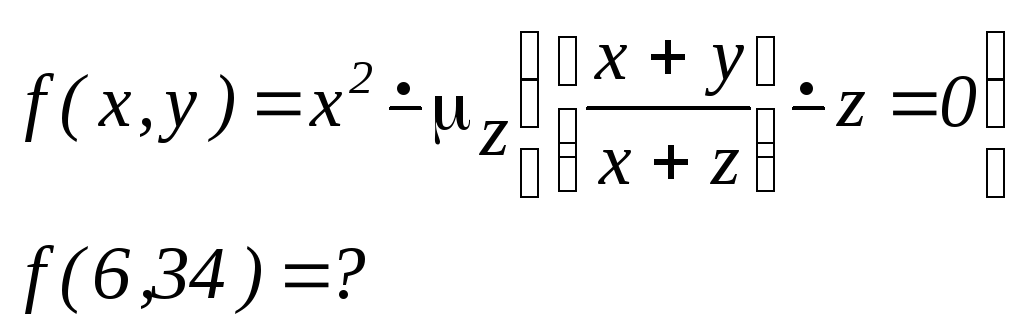
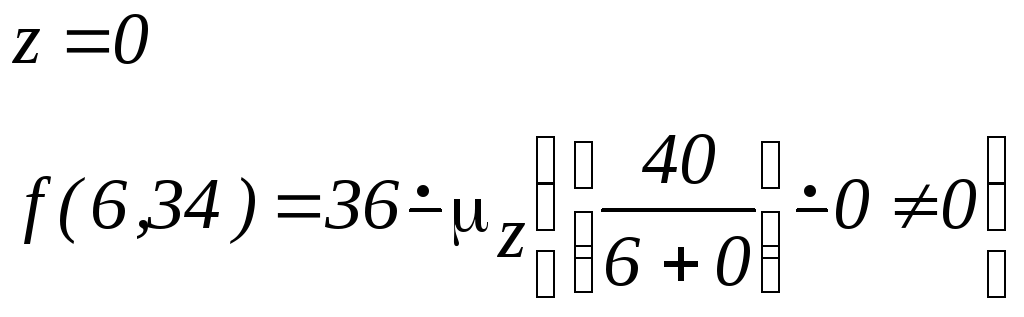
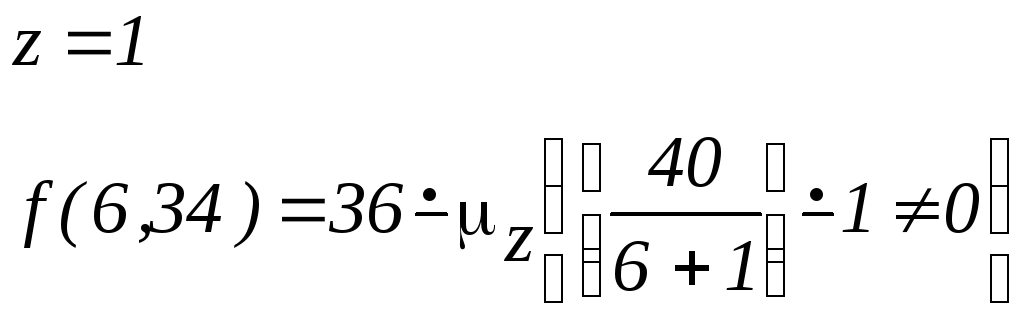
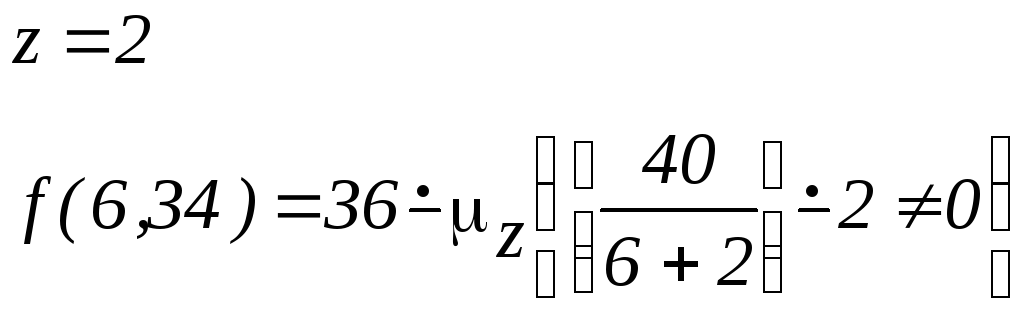
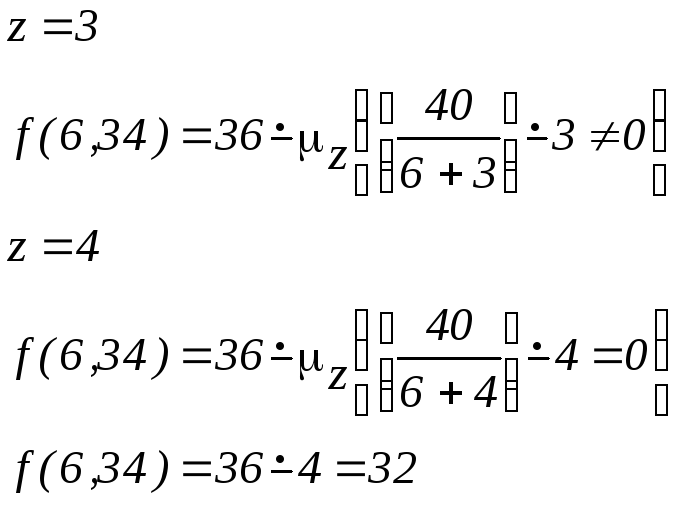
Пример 14. Оператор минимизации является удобным средством получения обратных функций: вычитание, деление, извлечение корня и т.д.:

.

.

.

.

Частично-рекурсивная функция – функция, которая может быть построена из простейших с помощью конечного числа применений оператора суперпозиции, примитивной рекурсии и минимизации.

Частично-рекурсивная функция является не всюду определенной, причем там, где она не определена, процесс ее вычисления продолжается бесконечно.

Общерекурсивная функция – всюду определенная частично-рекурсивная функция.

Связь между алгоритмами и рекурсивными функциями выражается тезисом Черча: какова бы ни была вычислимая неотрицательная целочисленная функция от неотрицательных целочисленных аргументов, существует тождественно равная ей частично-рекурсивная функция.

Класс частично-рекурсивных функций (ЧРФ) шире чем класс общерекурсивных функций (ОРФ), который в свою очередь шире классса примитивно-рекурсивных функций (ПРФ) (см. рис. 1).

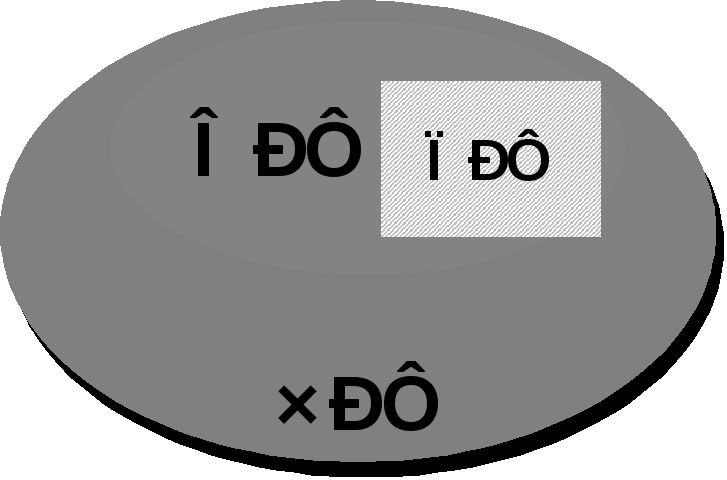
Рисунок 1 – Соотношение между классами частично-рекурсивных, общерекурсивных и примитивно-рекурсивных функций