3. Дискретная форма рядов Фурье

Рассмотрим разложение (6), (7). Предположим, что на отрезке функциязадана вm равностоящих узловых точках , где,

Используя для вычисления коэффициентов формулу левых прямоугольников из (7) имеем

или, учитывая ,

(8)

Соотношение (8) называется дискретным преобразованием Фурье.

Таким образом, учитывая окончательно имеем

Из соотношений (8) вытекают следующие свойства.

Свойство 1. Набор коэффициентов является комплексно сопряженным, т.е.

, ,

Действительно, согласно (8), имеем

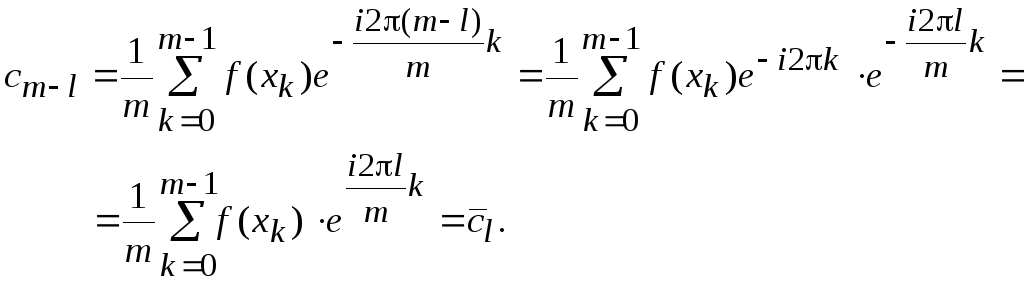
Свойство 2. Набор коэффициентов ,является периодическим с периодом равнымm. Т.е. .

Обосновывается аналогичным образом.

Следствие. Для построения разложения (8) при численном моделировании с равноотстоящими узловыми точками достаточно вычисления по коэффициентов.

Так, при m=3, например, - коэффициентов ,. Тогда по свойству 1,аПо свойству 2, -Приm=4 , - коэффициентов Тогда, и

8.4. Задание

1. Разложить указанные функции в ряд Фурье:

- в задачах 1 б), 2 б) представить разложение в стандартной форме;

- в задачах 1 а), 2 а) представить в комплексной форме.

2. Получить разложения указанных функций, используя стандартные процедуры пакета Matlab.

3. Сравнить полученные результаты для первых n гармоник.

Разложить указанные функции в ряд Фурье в указанных интервалах

Вариант 1

1. a), б) , по синусам,

2. а) б) по косинусам,

Вариант 2

1. a), б) , по косинусам,

2. а) , б) по синусам.

Вариант 3

1. a), б) 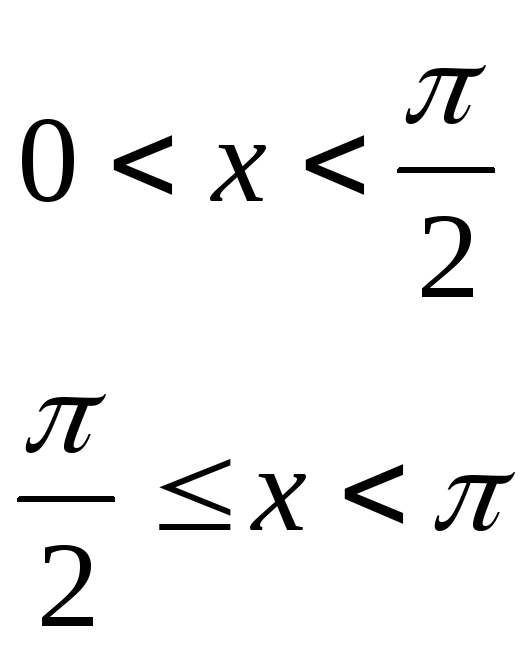, по косинусам,

2. а) , б) по синусам.

Вариант 4

1. a), б) , по синусам,

2. а) , б) , , по косинусам.

Вариант 5

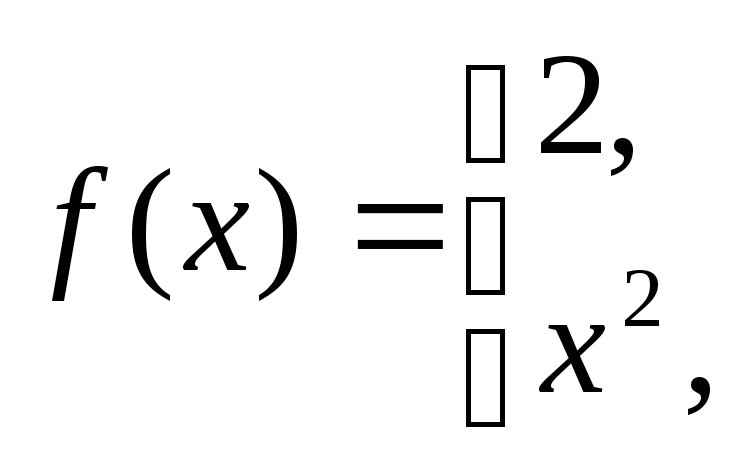
1. a) , б) , по косинусам,

2. а) , , б) , , по синусам.

Вариант 6

1. a) , б) , по косинусам,

2. а) , , б) , по косинусам.

Вариант 7

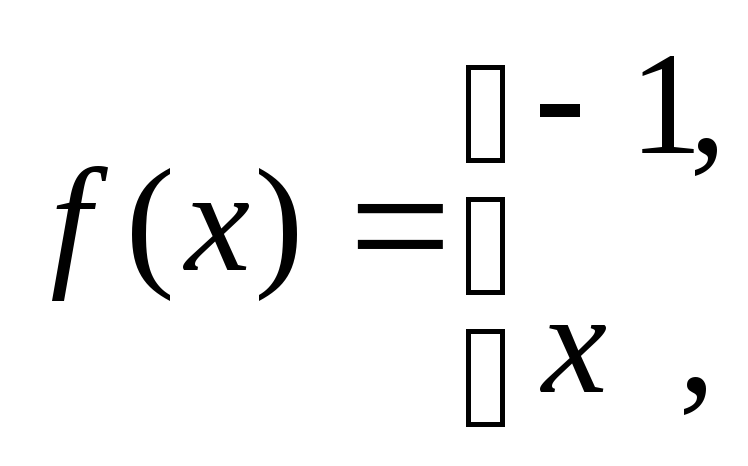
1. a) , б) , по косинусам,

2. а) , , б) , по синусам.

Вариант 8

1. a) , б) , по синусам,

2. а) , , б) , по косинусам.

Вариант 9

1. a), , б) , по косинусам,

2. а) , , б) по синусам.

Вариант 10

1. a) , б) , по косинусам,

2. a) , б) , по синусам.

Вариант 11

1. a) , б) , по синусам,

2. a) , б) , по косинусам.

Вариант 12

1. a), б) 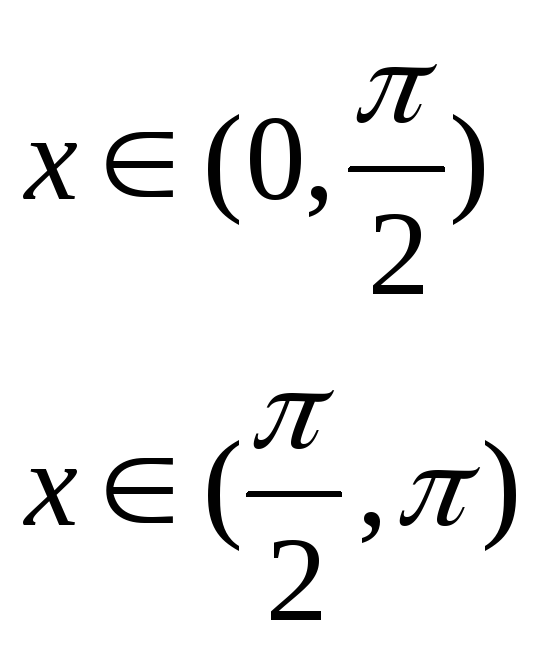по косинусам,

2. а) , б) по синусам.

Вариант 13

1. a), б) , по синусам,

2. а) б) по косинусам.

Вариант 14

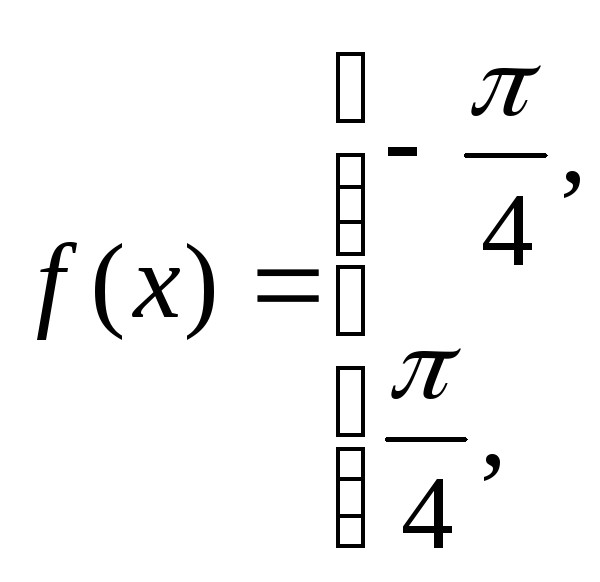
1. a) , б) , по косинусам,

2. а) , , б) , по синусам.

Вариант 15

1. a) , б) , по косинусам,

2. а) , , б) , по синусам.

Вариант 16

1. a) , б) , по синусам,

2. а) , , б) , по косинусам.

Вариант 17

1. a), б) по синусам,

2. а) , б) , , по косинусам.

Вариант 18

1. a) , б) , по косинусам,

2. a) , б) , по синусам

Вариант 19

1. a), б) , по синусам,

2. а) , б) , , по косинусам.

Вариант 20

1. a), б) по косинусам,

2. а) , б) , по синусам.

Вариант 21

1. a) , б) , по синусам,

2. а) , , б) , по косинусам.

Вариант 22

1. a) , б) , по косинусам,

2. а) , , б) , по синусам.

Вариант 23

1. a) , б) , по синусам,

2. а) , , б) , по косинусам.

Вариант 24

1. a) , б) , по косинусам,

2. а) , , б) 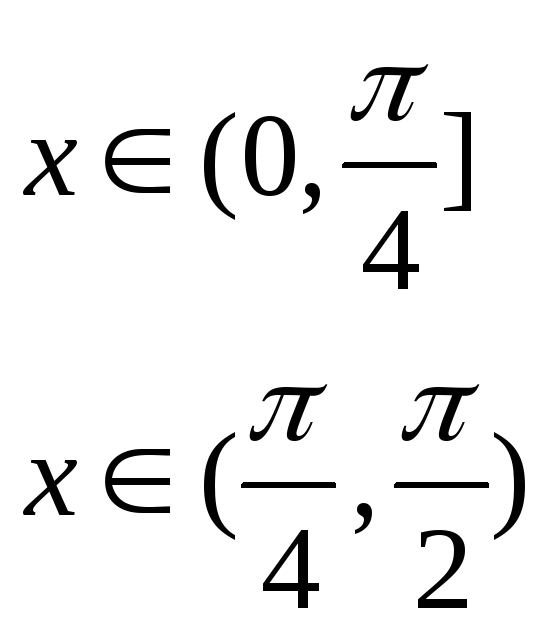по синусам.

Вариант 25

1. a), б) , по синусам,

2. а) , б) , , по косинусам.

Дополнительная литература

1. В.И. Крылов, В.В. Бобков, П.И. Монастырный. Вычислительные методы. В 2-х томах. – М. Наука, 1976.

2. Р.В. Хемминг. Численные методы для научных работников и инженеров. – М.: Мир, 1968.

3. Д.Н. Фаддеев, В.Н. Фаддеева. Вычислительные методы линейной алгебры. – СПб.: Издательство «Лань», 2002.

4. С.В. Поршнев. Вычислительная математика. Курс лекций. – СПб.: БХВ- Петербург, 2004.