3. Численные методы решения. Правило Рунге

Классификация методов. Производится в зависимости от особенностей той информации, которая используется при вычислении приближенного значения y(x) в узловой точке.

В первом приближении правило, по которому происходят вычисления символически можно представить в виде

(5)

где

- приближенные значения решения задачи (1), (2) в точках

h – шаг интегрирования. Если

1) , а, то правило (5) называется одношаговым, в противном случае,- многошаговым;

2) , вычислительное правило называетсяявным, при неявным, при , -с забеганием вперед.

Далее, основное внимание уделим одношаговым методам. Соответствующее вычислительное правило имеет вид

где .

Методы, основанные на разложении в ряд Тейлора. Предположим, что узлы интегрирования являются равноотстоящими, т.е. и рассмотрим участок. Предполагая функциюдифференцируемую достаточное число раз, имеем

(6)

Ограничиваясь малыми первого порядка относительно h, получим правило

(7)

которое называется явным методом Эйлера. Его погрешность на отрезке составляет

,

где , а на конечном отрезке [a, b] учитывая , равна

,

где . На основании этого данный метод называетсяметодом первого порядка точности. Он имеет наглядную геометрическую интерпретацию (Рисунок 1) и называется также методом ломаных. На каждом участке длиной h участок интегральной кривой заменяется отрезком прямой.

Рисунок 1. Явная схема Эйлера.

Замечание 1. Если воспользоваться разложением

(8)

и также ограничиться малыми первого порядка, получим правило

(9)

которое называется неявной схемой Эйлера.

Погрешность формулы (9) равна

,

погрешность метода на конечном промежутке

.

Замечание 2. Сложим (7), (9) и разделим на два, в результате чего получим новое правило

называемое методом трапеций. Также как и (9) оно является неявным. Если из разложения (6) почленно вычесть разложение (8), получим локальную погрешность формулы трапеций

.

Тогда погрешность, накапливаемая на отрезке будет равна

,

где . Таким образом, метод трапеций имеетвторой порядок точности.

Замечание 3. Рассмотренные выше погрешности приближенных методов описывают те ошибки, которые возникают вследствие замены дифференциального уравнения конечной вычислительной схемой и называется погрешностью аппроксимации. Помимо этого в общем балансе играют роль погрешности, возникающие на каждом шаге интегрирования в результате использования приближенного значения вместо точногоИх обычно относят к погрешностям обусловленным неточностями в задании исходных данных и рассматривают отдельно.

Методы Рунге-Кутта. Рассмотрим уравнение (1). Интегрируя его на промежутке получим

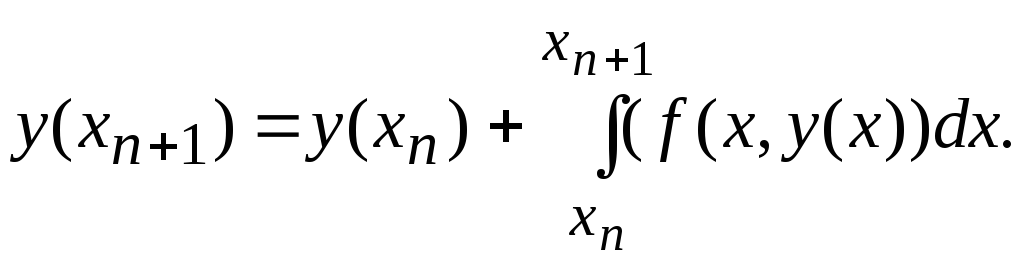
Тогда после замены , где, для приращения наn-ом шаге получим выражение

(10)

Таким образом, задача вычисления значения функции в точкесводится к вычислению интеграла в соотношении (10). Однако использование традиционных квадратурных формул для этих целей проблематично, так как значения неизвестны. В методах Рунге – Кутта квадратурные схемы строятся следующим образом.

Вводятся три группы параметров , где

,

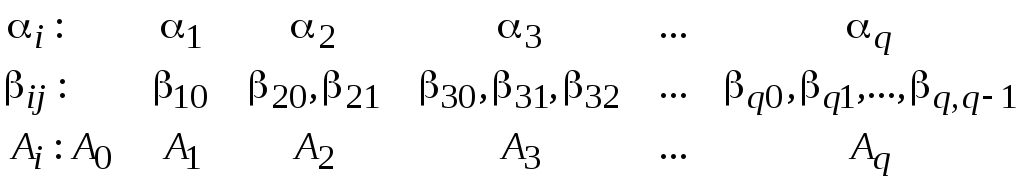которыми распоряжаются так. Первая группа параметров определяет набор узловых значений по первой переменной подинтегральной функции. Вторая группа параметров определяет набор узловых значений по ее второй переменной. Причем производится это косвенным образом через приращенияфункциив предыдущих узловых точках, где

,

,

,

. . . . . . . .

.

Наконец, третья группа параметров используется для формирования квадратурной формулы

.

Таким образом, окончательно

(11)

Обозначим погрешность соотношения (11) через , т.е.

или

Представим ее с помощью формулы Тейлора в виде разложения по степеням h

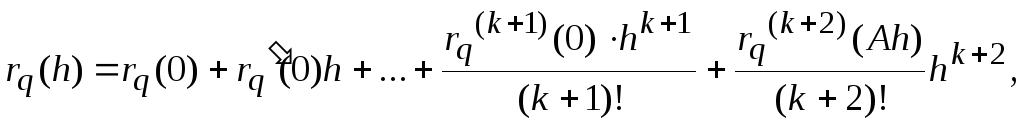
где .

Если потребовать теперь, чтобы получим погрешность соотношения (11) равнуюи, следовательно, погрешность метода равную.

К числу наиболее употребительных относятся методы 4-го порядка точности. Для них значение . Один из вариантов соответствующего набора параметров следующий

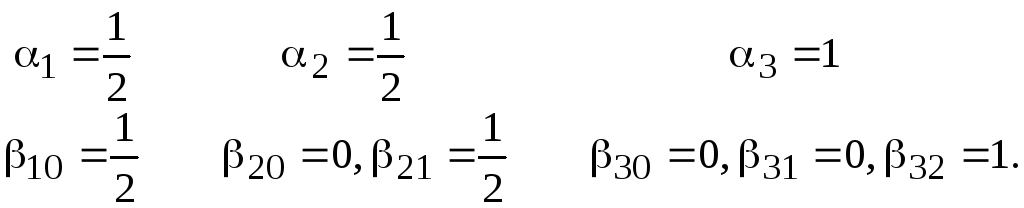
Тогда выражения имеют вид

,

,

,

коэффициенты ,-

, ,,

и вычислительное правило, в целом,

.

На Рисунке 2 в полосе указаны используемые в этом методе узловые точки. Значениявыбраны произвольно.

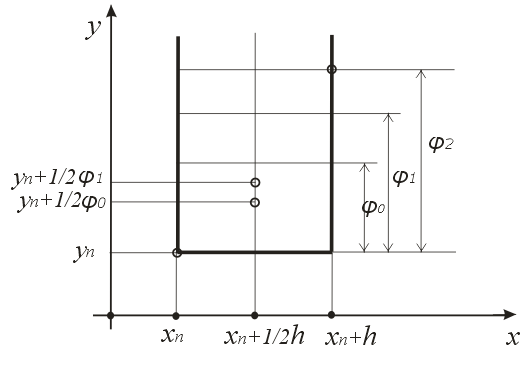
Рисунок 2. Узловые точки метода Рунге-Кутта 4-го порядка

Правило Рунге. Для оценки погрешности численных результатов интегрирования при использовании одношаговых методов на практике обычно применяют правило Рунге, которое заключается в следующем.

Теоретически показано, что главный член погрешности аппроксимации имеет вид , гдеk – порядок метода, - некоторая функция, определяемая особенностями правой части дифференциального уравнения.

,

где , - точное значение,, приближенное, определенное при проведении расчетов с шагомh. Тогда, проводя расчеты с шагом и, получаем

.

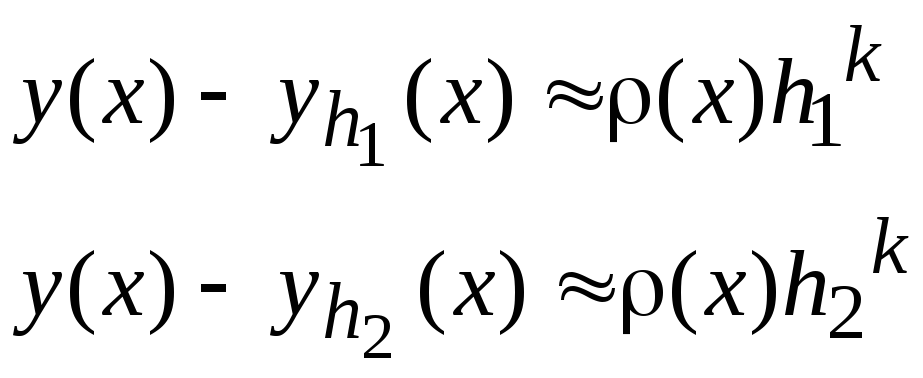Разрешая, далее, приближенную систему этих соотношений относительно , имеем

,

откуда

. (12)

Соотношение (12) и представляет правило Рунге. Естественно, оно дает достоверные результаты лишь в том случае, когда доминирующей в общей погрешности результата является погрешность метода.

Обычно правило (12) используют при ,. Тогда

.

В частности, для методов Эйлера (k=1)

,

метода трапеций (k=2), -

,

метода Рунге – Кутта четвертого порядка (k=4),-

.