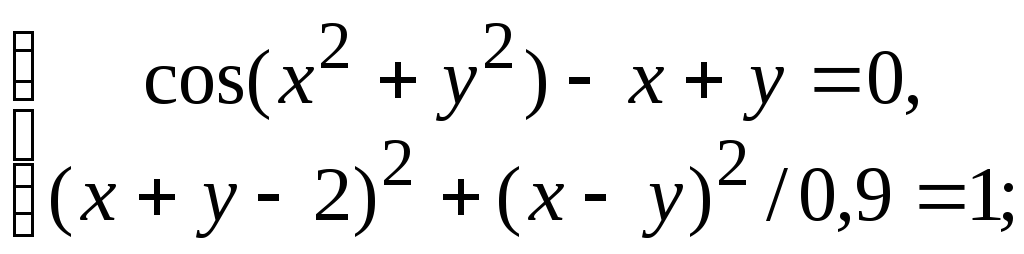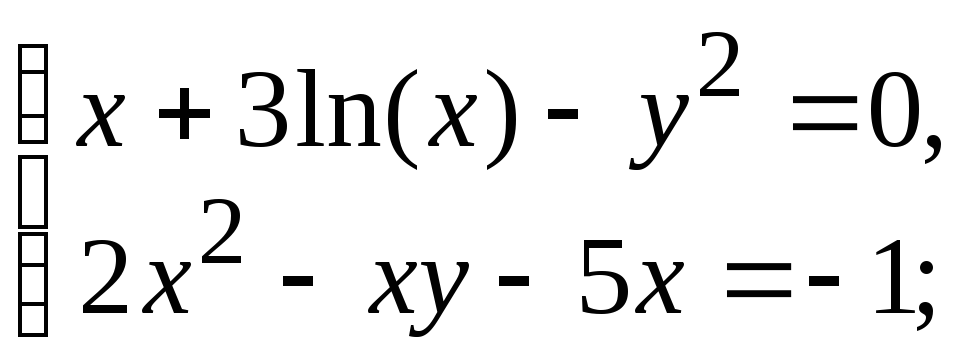- •В. Н. Беловодский Восемь лекций по численным методам
- •7.080407 «Компьютерный эколого-экономический мониторинг»)
- •Содержание
- •Введение
- •Лекция 1.Элементы теории погрешностей
- •.Типы и источники погрешностей
- •1.2.Абсолютные и относительные погрешности приближённых чисел
- •1.3. Погрешности выполнения арифметических операций
- •.Погрешность вычисления функции
- •1.5.Запись приближённых чисел
- •1.6.Правила действий над приближёнными числами
- •1.7.Погрешности при машинном представлении чисел
- •1.8. Варианты индивидуальных заданий
- •Лекция 2. Интерполяция функций
- •2.1. Постановка задачи
- •2.2. Алгебраическая интерполяция, существование и единственность интерполяционного многочлена
- •2.3. Интерполяционный многочлен Лагранжа
- •2.4. Конечные и разделенные разности
- •2.5. Интерполяционный многочлен Ньютона
- •2.6. Сравнительный анализ интерполяционных многочленов
- •2.7. Погрешности интерполяционных формул
- •2.8. Интерполяционные формулы для равноотстоящих узлов
- •2.9. Сплайн – интерполяция
- •2. 10. Варианты индивидуальных заданий
- •Лекция 3. Методы решения систем линейных алгебраических уравнений
- •3.1. Предварительные замечания
- •3.2. Точные методы решения
- •3.3. Приближённые методы решения
- •3.4. Сходимость и погрешность приближённых методов
- •3.6. Варианты индивидуальных заданий
- •Лекция 4. Решение нелинейных уравнений
- •4.1. Предварительные замечания
- •4.2. Методы, основанные на алгебраическом интерполировании
- •4.3. Метод последовательных приближений
- •4.4. Задание
- •Лекция 5. Решение систем нелинейных уравнений
- •Метод итераций
- •Метод Ньютона
- •5.3. Сравнительный анализ методов
- •5.4. Задание
- •Требования к программе
- •Требования к отчету
- •Лекция 6. Приближенное вычисление определенных интегралов
- •6.1. Вступительные замечания
- •6.2. Формулы Ньютона-Котеса
- •6.3. Простейшие квадратурные правила
- •6.4. Погрешности квадратурных формул
- •6.5. Понятие о методах Монте–Карло
- •6.6. Задание
- •Варианты заданий
- •Лекция 7. Методы решения обыкновенных дифференциальных уравнений
- •Вступительные замечания
- •Аналитические методы
- •Численные методы решения. Правило Рунге
- •Задание
- •Лекция 8. Основы спектрального анализа
- •Элементы общей теории
- •Дискретная форма рядов Фурье
- •8.4. Задание
Требования к отчету
Отчет должен содержать следующие обязательные пункты:
титульный лист установленного образца;
формулировку задания;
краткие теоретические сведения о применяемых методах;
графики функций;
результаты расчетов: ручного и при помощи программы;
текст программы;
выводы.
Варианты к заданию
Лекция 6. Приближенное вычисление определенных интегралов
В которой формулируются основные идеи, реализованные при приближенном вычислении определенных интегралов, рассмотрены простейшие квадратурные формулы для равноотстоящих узлов, обсуждаются вопросы погрешности. Дано понятие о методах Монте-Карло.
6.1. Вступительные замечания
Ниже рассматриваются методы приближенного интегрирования собственных интегралов Римана
![]() . (1)
. (1)
Традиционный подход заключается в следующем.
На отрезке [a,
b]
выбирается ряд узловых точек
![]() и значение
интеграла представляется в виде линейной
комбинации значений подинтегральной
функции в узловых точках
и значение
интеграла представляется в виде линейной
комбинации значений подинтегральной
функции в узловых точках
 ,
,
которая называется
квадратурной
формулой.
При заданном числе n расположение узлов
и значения
коэффициентов
![]() подбирается так, чтобы обеспечивалась
наивысшая точность результата. Наиболее
просты и употребительны методы, в которых
узловые точки выбираются равноотстоящими.
На их рассмотрении далее мы и остановимся.
подбирается так, чтобы обеспечивалась
наивысшая точность результата. Наиболее
просты и употребительны методы, в которых
узловые точки выбираются равноотстоящими.
На их рассмотрении далее мы и остановимся.
6.2. Формулы Ньютона-Котеса
Предположим, что
отрезок [a,
b]
разделен на
n
равных частей величиной
![]() и обозначим точки деления через
и обозначим точки деления через
![]() .
Представим подинтегральную функцию
(1) с помощью многочлена Лагранжа
.
Представим подинтегральную функцию
(1) с помощью многочлена Лагранжа

где t
=
 .
.
Тогда
 (2)
(2)
или
 ,
,
где
 (3)
(3)
Соотношения (2),
(![]() )и называются
квадратурными
формулами Ньютона-Котеса.
)и называются
квадратурными
формулами Ньютона-Котеса.
В случае, когда
деление отрезка [a,b]
не производится и на нем выбирается
единственная узловая точка, обозначим
ее через
![]() ,
интерполяционный многочлен принимает
вид
,
интерполяционный многочлен принимает
вид![]() ,
а квадратурная формула, –
,
а квадратурная формула, –
![]() .
(4)
.
(4)
Рассмотрим другие простейшие случаи, предварительно обосновав важное, для вычисления коэффициентов Hi, свойство:
При фиксированном
n
значения Hi
и Hn-i,
где
![]() ,равны.
,равны.
Доказательство.
Пусть n=2m.
Не умаляя общности можно считать, что
![]() .
Рассмотрим числитель подинтегральной
функции из соотношения (2)
.
Рассмотрим числитель подинтегральной
функции из соотношения (2)
![]() (t)=t(t-1)…
(t-i)…
(t-m)…
(t-(2m-i))…
(t-2m).
(t)=t(t-1)…
(t-i)…
(t-m)…
(t-(2m-i))…
(t-2m).
Удалим из![]() (t)
множители (t-i)
и (t-(2m-i))
и обозначим
произведение оставшихся , – через
(t)
множители (t-i)
и (t-(2m-i))
и обозначим
произведение оставшихся , – через
![]() .
Т.е.
.
Т.е.
![]() (t)=(t-i)
(t-(2m-i))
(t)=(t-i)
(t-(2m-i))
![]() (t).
(t).
Тогда

и

Сделаем в последних интегралах замену t-m=z или t=z+m. Тогда
![]()
и является нечетной
функцией переменной z. Выражения для
определения ![]() ,
,
![]() после очевидных преобразований примут
вид
после очевидных преобразований примут
вид
 ,
,
 .
.
Вторые слагаемые
в фигурных скобках, в силу нечетности
![]() (z),
равны 0, а числа2m-i
и
i
имеют
одинаковую четность. Поэтому
(z),
равны 0, а числа2m-i
и
i
имеют
одинаковую четность. Поэтому
![]() ,
что и требовалось.
,
что и требовалось.
Случай n=2m + 1 рассматривается аналогично.
Вернемся к вычислению
коэффициентов ![]() .
.
Рассмотрим n=1. Тогда из (3) следует
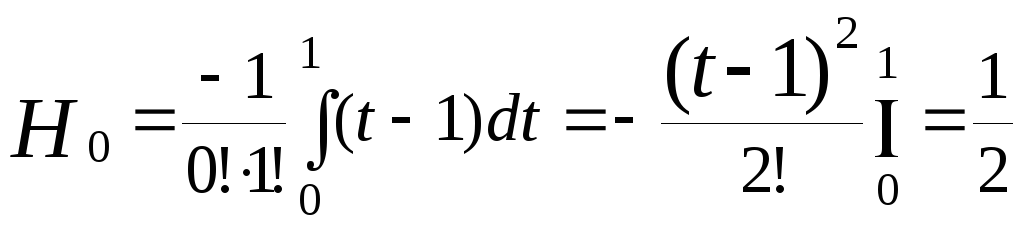 .
.
Отсюда
![]() и квадратурная формула (2) принимает вид
и квадратурная формула (2) принимает вид
![]() (5)
(5)
Пусть теперь n=2 Из (3) имеем
![]() ,
,
![]() .
.
Тогда
![]() =
=![]() =
=![]()
и
![]() (6)
(6)
Рассмотрим n=3. Согласно (3)
![]() ,
,
следовательно, и
![]() ,
,
 ,
,
следовательно, и
![]() .
.
Тогда квадратурная формула (2) принимает вид
 (7)
(7)