
- •«Методические указания и контрольные задания по общему курсу физики с примерами решения задач для студентов заочников. Раздел «Электромагнетизм»
- •«Методические указания и контрольные задания по общему курсу физики с примерами решения задач для студентов заочников. Раздел «Электромагнетизм»
- •1. Рабочая программа по разделу ”Электромагнетизм”.
- •2.Методические указания к решению задач и выполнению контрольных работ.
- •3.Основные законы и формулы
- •4.Примеры решения задач
- •9,98*10-3С.
- •36,03(А/м)
- •4,03·10 27(М-3)
- •6,2·10-3(М/с)
- •5.Задачи для самостоятельного решения
- •6.Вопросы для контроля знаний
- •1. 2. 3. 4.
- •1. 2. 3. 4.
- •1..2..3.. 4..
- •1. . 2. .3. .4. .
- •1. 2. 3. 4.
- •1. 2. 3. 4.
- •1. 2. 3. 4.
- •1. 2. 3. 4.
- •7.Ответы на вопросы для самоконтроля
- •8.Варианты индивидуальных заданий
- •9.Приложения
- •9.1. Фундаментальные физические постоянные
- •9.2. Десятичные приставки к названиям единиц
- •9.3. Плотность твердых тел
- •9.4. Удельное сопротивление металлов
- •10.Рекомендуемая литература
3.Основные законы и формулы
Механический момент, действующий на контур с током, помещенный в однородное магнитное поле,
![]() ,
,
где
![]() -магнитная
индукция;
-магнитная
индукция;
 -магнитный
момент контура с током:
-магнитный
момент контура с током:
![]() ,
,
где
S
– площадь контура с током;
![]() -единичный
вектор нормали к поверхности контура;
-единичный
вектор нормали к поверхности контура;
I –сила тока.
Связь
магнитной
индукции
![]() и
напряженности
и
напряженности![]() магнитного поля
магнитного поля
![]() ,
,
где
![]() -
магнитная постоянная, µ- магнитная
проницаемость
среды.
-
магнитная постоянная, µ- магнитная
проницаемость
среды.
Закон Био — Савара — Лапласа
![]() ,
,
где
d![]() -
магнитная индукция поля, создаваемая
элементом длинны dl
проводника с током I;
-
магнитная индукция поля, создаваемая
элементом длинны dl
проводника с током I;
![]() -
радиус-вектор, проведенный от dl
к точке, в которой определяется магнитная
индукция.
-
радиус-вектор, проведенный от dl
к точке, в которой определяется магнитная
индукция.
Модуль
вектора d![]()
dB=![]() ,
,
где
a-
угол между векторами d![]() и
и
![]() .
.
Принцип суперпозиции магнитных полей
![]() ,
,
где
![]() - магнитная индукция результирующего
поля;
- магнитная индукция результирующего
поля;![]() магнитные индукции складываемых полей.
магнитные индукции складываемых полей.
Магнитная индукция поля, создаваемого бесконечно длинным прямым проводником с током,
![]() ,
,
где R – расстояние от оси проводника.
Магнитная индукция поля, создаваемого прямым проводником с током конечных размеров, в произвольной точке A
![]() ,
,
где
R-
расстояние от точки A
до проводника;
![]() -
углы, образованные радиусом-вектором,
проведенным в точкуA
соответственно из начала и конца
проводника, с направлением тока.
-
углы, образованные радиусом-вектором,
проведенным в точкуA
соответственно из начала и конца
проводника, с направлением тока.
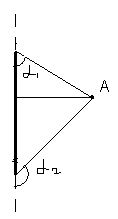
Рис.3.1
Магнитная индукция в центре кругового проводника с током
![]() ,
,
где R- радиус кривизны проводника.
Магнитная индукция в точке, лежащей на оси кругового тока на расстоянии h от его центра,

Закон Ампера
![]() ,
,
где
![]() -
сила, действующая на элемент длины
-
сила, действующая на элемент длины
![]() проводника
с током I,
помещенный в магнитное поле с индукцией
проводника
с током I,
помещенный в магнитное поле с индукцией
![]() .
.
Модуль силы Ампера
dF
= IBdl
sin![]() ,
,
где
![]() - угол
между векторами
- угол
между векторами
![]() и
и
![]() .
.
Сила взаимодействия двух прямых бесконечных прямолинейных параллельных проводников с токами I1 и I2
![]() ,
,
где
R
- расстояние между проводниками;
![]() -
отрезок проводника.
-
отрезок проводника.
Сила Лоренца
![]() ,
,
где
![]() -
сила, действующая на заряд Q,
движущийся в магнитном
поле со скоростью
-
сила, действующая на заряд Q,
движущийся в магнитном
поле со скоростью
![]() .
.
Формула Лоренца
![]() ,
,
где
![]() -
результирующая
сила, действующая на движущийся
заряд Q,
если на него действуют электрическое
поле напряженностью
-
результирующая
сила, действующая на движущийся
заряд Q,
если на него действуют электрическое
поле напряженностью
![]() и
магнитное поле индукцией
и
магнитное поле индукцией
![]() .
Холловская поперечная разность
потенциалов
.
Холловская поперечная разность
потенциалов
![]()
где B – магнитная индукция; I – сила тока; d – толщина пластинки;
![]() постоянная
Холла (n
– концентрация электронов).
постоянная
Холла (n
– концентрация электронов).
Закон
полного тока для магнитного поля в
вакууме (теорема о циркуляции вектора
![]() )
)
![]()
где
![]() -магнитная
постоянная;
-магнитная
постоянная;
![]() -вектор
элементарной
длины контура, по направлению совпадающий
с обходом
контура;
-вектор
элементарной
длины контура, по направлению совпадающий
с обходом
контура;
![]() составляющая
вектора
составляющая
вектора
![]() в
направлении касательной к контуру L
произвольной формы
(с учетом выбранного направления обхода);
α - угол
между векторами
в
направлении касательной к контуру L
произвольной формы
(с учетом выбранного направления обхода);
α - угол
между векторами
![]() и
и![]() ;
;![]() -алгебраическая
сумма
токов, охватываемых контуром.
-алгебраическая
сумма
токов, охватываемых контуром.
Магнитная индукция поля внутри соленоида (в вакууме), имеющего N
витков,
![]()
где
![]() - длина соленоида.
- длина соленоида.
Магнитная индукция поля внутри тороида (в вакууме)
![]() .
.
Поток вектора магнитной индукции (магнитный поток) через площадку dS
![]()
где
![]() =
=![]() -вектор,
модуль которого равен dS,
а
направление
-вектор,
модуль которого равен dS,
а
направление
совпадает
с нормалью
![]() к площадке; Вn
- проекция
вектора
к площадке; Вn
- проекция
вектора
![]() на
на
направление нормали к площадке.
Поток вектора магнитной индукции сквозь произвольную поверхность S
![]()
Работа по перемещению проводника с током в магнитном поле
dA = IdФ,
где dФ - магнитный поток, пересеченный движущимся
проводником.
Закон Фарадея
εi
=
![]()
где εi - ЭДС индукции.
ЭДС индукции, возникающая в рамке площадью S при вращении рамки с угловой скоростью
 в однородном
магнитном поле с индукцией В,
в однородном
магнитном поле с индукцией В,
εi = BSω sin ωt,
где
ωt
- мгновенное
значение угла между вектором
![]() ивектором
нормали
ивектором
нормали
![]() к плоскости рамки.
к плоскости рамки.
Магнитный
поток, создаваемый током
![]() в
контуре синдуктивностью
L,
в
контуре синдуктивностью
L,
Ф = LI.
ЭДС самоиндукции
εs
=
![]()
где L - индуктивность контура.
Индуктивность соленоида
![]()
где N - число витков соленоида; I - его длина.
Сила тока соответственно при размыкании и замыкании цепи
![]() и
и
![]()
где τ = L/R - время релаксации (L - индуктивность;
R - сопротивление).
ЭДС взаимной индукции (ЭДС, индуцируемая изменением силы тока в соседнем контуре)
εв
=
![]()
где L12 - взаимная индуктивность контуров.
Взаимная индуктивность двух катушек (с числом витков N1 и N2), намотанных на общий тороидальный сердечник,
![]()
где μ - магнитная проницаемость сердечника; l — длина сердечника по средней линии; S — площадь сердечника.
Энергия магнитного поля, создаваемого током в замкнутом контуре, по которому течет ток I,
![]()
Объемная плотность энергии однородного магнитного поля длинного соленоида
![]()
Связь орбитального магнитного

 и орбитальногомеханического
Ll
моментов электрона
и орбитальногомеханического
Ll
моментов электрона
![]()
где
![]() -гиромагнитное
отношение орбитальных моментов.
-гиромагнитное
отношение орбитальных моментов.
Намагниченность
![]()
где
![]() -магнитный
момент магнетика, равный векторной
сумме магнитных моментов отдельных
молекул
(атомов).
-магнитный
момент магнетика, равный векторной
сумме магнитных моментов отдельных
молекул
(атомов).
Связь между намагниченностью и напряженностью магнитного поля
![]()
где χ - магнитная восприимчивость вещества.
Связь
между векторами
![]()
![]()
где
![]() -магнитная
постоянная.
-магнитная
постоянная.
Связь между магнитной проницаемостью и магнитной восприимчивостью вещества
μ = 1 + χ.
