
- •2010 Г.
- •Глава 1. Элементы математической логики и теории
- •Глава 2. Элементы линейной алгебры
- •Глава 3. Векторная алгебра
- •Глава 4. Аналитическая геометрия на плоскости
- •Глава 5. Аналитическая геометрия в пространстве
- •Глава 1. Элементы математической логики и теории множеств
- •1.1. Аксиоматический метод
- •1.2. Алгебра высказываний
- •1.3. Логика предикатов
- •1.4. Множества и их элементы
- •1.5. Операции над множествами
- •1.6. Отображения множеств
- •1.7. Мощность множества
- •Глава 2. Элементы линейной алгебры
- •2.1. Системы линейных уравнений
- •2.2. Матрицы и действия над ними
- •2.3. Запись систем в матричной форме и их решение
- •2.4. Определители и их свойства
- •2.5. Правило Крамера
- •2.6. Решение системы линейных уравнений снеизвестными методом Гаусса
- •2.7. Теорема Кронекера-Капелли
- •2.8. Обратная матрица
- •2.9. Векторное пространство
- •Глава 3. Векторная алгебра
- •3.1. Система координат на прямой, на плоскости и в пространстве
- •3.2. Векторы и линейные операции над ними
- •3.3. Скалярное произведение векторов
- •3.4. Векторное произведение двух векторов
- •3.5. Смешанное произведение трех векторов
- •Глава 4. Аналитическая геометрия на плоскости
- •4.1. Уравнение линии в заданной системе координат
- •4.2. Различные формы уравнения прямой на плоскости
- •4.3. Основные задачи на прямую на плоскости
- •4.4. Окружность
- •4.5. Эллипс
- •4.6. Гипербола
- •4.7. Парабола
- •4.8. Классификация кривых второго порядка
- •4.9. Построение эллипса, гиперболы, параболы
- •4.10. Кривые второй степени и конические сечения
- •Глава 5. Аналитическая геометрия в пространстве
- •5.1. Поверхности и линии в пространстве
- •5.2. Уравнение плоскости в пространстве
- •5.3. Основные задачи о положении плоскости
- •5.4. Уравнения прямой в пространстве
- •5.5. Основные задачи о положении прямой
- •5.6. Задачи на взаимное расположение прямой и плоскости
- •5.7. Цилиндрические и конические поверхности
- •5.8. Поверхности вращения
- •5.9. Технические приложения геометрических свойств поверхности
Глава 5. Аналитическая геометрия в пространстве
В предыдущей главе мы познакомились с уравнением линии и прямой линии на плоскости, с кривыми второй степени, изучили вопросы, связанные с их положением. Настоящая глава посвящена аналогичным проблемам, но уже в пространстве.
5.1. Поверхности и линии в пространстве
В декартовой системе координат каждой точке пространства соответствует тройка действительных чисел и наоборот.
Так
же, как это делалось при изучении линий
на плоскости, поверхность рассматривают
как геометрическое место точек,
обладающих некоторым общим свойством.
Обозначая через
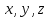 координаты точки в декартовой системе
координат, мы выражаем посредством
уравнения между ними свойство, общее
всем точкам поверхности и только им.
Такое уравнение называется уравнением
поверхности, а входящие в него координаты
координаты точки в декартовой системе
координат, мы выражаем посредством
уравнения между ними свойство, общее
всем точкам поверхности и только им.
Такое уравнение называется уравнением
поверхности, а входящие в него координаты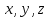 - текущими координатами.
- текущими координатами.
Пример
5.1.
Уравнение сферы радиуса
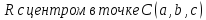 имеет вид:
имеет вид: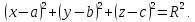
Пример
5.2.
Пусть уравнение не содержит переменной
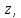 то есть имеет вид:
то есть имеет вид: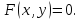 На координатной плоскости xOy это уравнение
определяет некоторую линию
На координатной плоскости xOy это уравнение
определяет некоторую линию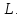 Но ему удовлетворяют координаты всех
тех точек в пространстве, у которых две
первые координаты совпадают с координатами
любой точки линии
Но ему удовлетворяют координаты всех
тех точек в пространстве, у которых две
первые координаты совпадают с координатами
любой точки линии .
Совокупность таких точек есть
поверхность, описанная прямой,
параллельной оси Oz и пересекающей
линию
.
Совокупность таких точек есть
поверхность, описанная прямой,
параллельной оси Oz и пересекающей
линию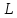 (рис.5.1).
(рис.5.1).
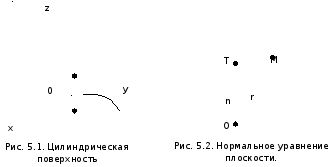

Всякую
линию в пространстве можно рассматривать
как пересечение двух поверхностей.
Пусть
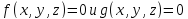 есть уравнение тех поверхностей,
пересечение которых дает линию
есть уравнение тех поверхностей,
пересечение которых дает линию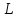 .
Координаты любой ее точки удовлетворяют
обоим уравнениям, так как эти точки
лежат одновременно на обеих поверхностях.
Верно и обратное, система двух уравнений
указанного вида определяет, вообще
говоря, в пространстве линию как
геометрическое место точек, координаты
которых удовлетворяют этой системе.
.
Координаты любой ее точки удовлетворяют
обоим уравнениям, так как эти точки
лежат одновременно на обеих поверхностях.
Верно и обратное, система двух уравнений
указанного вида определяет, вообще
говоря, в пространстве линию как
геометрическое место точек, координаты
которых удовлетворяют этой системе.
5.2. Уравнение плоскости в пространстве
Рассмотрим теперь простейшую поверхность - плоскость и несколько способов ее задания.
Положение
плоскости в пространстве полностью
определяется ее расстоянием
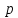 от точки
от точки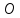 (длинной перпендикуляра
(длинной перпендикуляра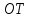 ,
опущенного из точки
,
опущенного из точки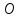 на плоскость), и единичным вектором
на плоскость), и единичным вектором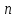 ,
перпендикулярным плоскости и направленным
от точки
,
перпендикулярным плоскости и направленным
от точки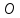 к плоскости (рис.5.2). Когда точка
к плоскости (рис.5.2). Когда точка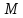 движется по плоскости, то ее радиус
вектор
движется по плоскости, то ее радиус
вектор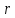 меняется
так, что
меняется
так, что
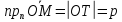 .
(5.1)
.
(5.1)
Это
условие имеет место для всех точек
плоскости и лишь для них. Но
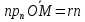 ,
следовательно, уравнение (5.1) может быть
переписано в виде:
,
следовательно, уравнение (5.1) может быть
переписано в виде:
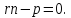 (5.2)
(5.2)
Это уравнение называется нормальным уравнением плоскости.
Переходя
в уравнении (5.2) к координатам и помещая
их начало в точку
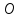 ,
заметим, что проекции единичного вектора
,
заметим, что проекции единичного вектора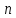 на координатные оси равны его направляющим
косинусам, а проекциями радиуса-вектора
на координатные оси равны его направляющим
косинусам, а проекциями радиуса-вектора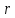 точки
точки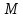 служат её координаты
служат её координаты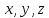 .
Выражая скалярное произведение
.
Выражая скалярное произведение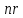 через их координаты, получим:
через их координаты, получим:
 .
(5.3)
.
(5.3)
Уравнение
(5.3) называется нормальным
уравнением плоскости в канонической
форме.
Его степень относительно
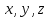 равна единице, следовательно, всякую
плоскость можно задать уравнением
первой степени относительно текущих
координат.
равна единице, следовательно, всякую
плоскость можно задать уравнением
первой степени относительно текущих
координат.
Заметим,
что уравнения (5.2) и (5.3) верны и тогда,
когда
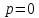 ,
т.е. плоскость проходит через начало
координат. В этом случае за
,
т.е. плоскость проходит через начало
координат. В этом случае за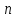 можно принять любой из двух единичных
векторов, перпендикулярных к плоскости
(они отличаются знаком).
можно принять любой из двух единичных
векторов, перпендикулярных к плоскости
(они отличаются знаком).
Покажем теперь, что всякое уравнение первой степени между тремя переменными определяет плоскость. Возьмем уравнение первой степени общего вида:
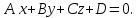 (5.4)
(5.4)
Будем
рассматривать
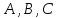 как проекции некоторого вектора
как проекции некоторого вектора на оси координат, а
на оси координат, а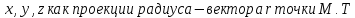 огда
уравнение (5.4) может быть переписано в
векторной форме в следующем виде:
огда
уравнение (5.4) может быть переписано в
векторной форме в следующем виде:
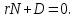 (5.5)
(5.5)
Покажем, что уравнение (5.5) может быть приведено к нормальному виду (5.2). Рассмотрим следующие случаи.
1)
Пусть
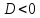 .
Разделим уравнение (5.5) на модуль вектора
.
Разделим уравнение (5.5) на модуль вектора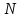 ,
получим:
,
получим: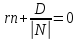 ,
так как
,
так как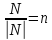 .
Обозначив
.
Обозначив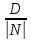 через
через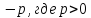 ,
получим нормальное уравнение
,
получим нормальное уравнение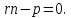
2)
Если
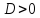 ,
то разделим уравнение (5.5) на
,
то разделим уравнение (5.5) на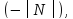 после чего оно примет вид:
после чего оно примет вид: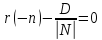 .
Обозначив
.
Обозначив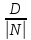 через
через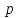 ,
получим нормальное уравнение.
,
получим нормальное уравнение.
3)
Если
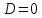 ,
то уравнение (5.5) можно разделить как
на
,
то уравнение (5.5) можно разделить как
на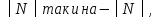 в первом случае мы получим
в первом случае мы получим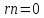 ,
во втором -
,
во втором -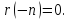 Каждое из них является нормальным
уравнением.
Каждое из них является нормальным
уравнением.
Таким образом, уравнение (5.5) всегда может быть приведено к нормальному виду (5.2). Но нормальное уравнение определяет плоскость. Следовательно, уравнение (5.5), а значит и исходное уравнение (5.4), определяют плоскость.
Уравнение (5.4) называется общим уравнением плоскости.
Всякий
вектор, отличный от нуля и перпендикулярный
к плоскости, называется
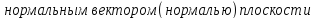 . Тогда,
очевидно, вектор
. Тогда,
очевидно, вектор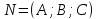 будет одним из нормальных векторов
плоскости. Таким образом, коэффициенты
будет одним из нормальных векторов
плоскости. Таким образом, коэффициенты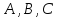 при текущих координатах в уравнении
(5.4) имеют простой геометрический смысл:
они являются проекциями нормального
вектора на оси координат. Смысл свободного
члена
при текущих координатах в уравнении
(5.4) имеют простой геометрический смысл:
они являются проекциями нормального
вектора на оси координат. Смысл свободного
члена заключается в том, что его абсолютная
величина, разделенная на длину нормального
вектора, равна расстоянию от плоскости
до начала координат.
заключается в том, что его абсолютная
величина, разделенная на длину нормального
вектора, равна расстоянию от плоскости
до начала координат.
Если за нормаль плоскости выбран единичный вектор, направленный из начала координат перпендикулярно к данной плоскости, то уравнение (5.5) превращается в нормальное.
Чтобы
привести общее уравнение плоскости
к нормальному виду, надо его разделить
на длину вектора
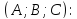 взяв ее со знаком + или -, смотря по тому,
будет ли свободный член
взяв ее со знаком + или -, смотря по тому,
будет ли свободный член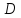 отрицательным или положительным. Иными
словами, для приведения общего уравнения
(5.5) к нормальному виду надо умножить
его на
отрицательным или положительным. Иными
словами, для приведения общего уравнения
(5.5) к нормальному виду надо умножить
его на
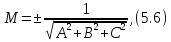
причем
знак множителя надо брать противоположным
знаку свободного члена
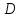 .
После умножения на
.
После умножения на уравнение
(5.5) принимет вид:
уравнение
(5.5) принимет вид: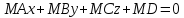 и совпадет с нормальным уравнением
(5.3). Следовательно:
и совпадет с нормальным уравнением
(5.3). Следовательно:
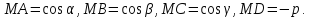 (5.7)
(5.7)
Подставляя
значение
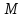 из (5.6) в эти равенства, получаем:
из (5.6) в эти равенства, получаем:
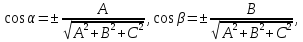
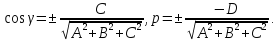
Если
 то в этих формулах берется знак "+",
иначе "-".
то в этих формулах берется знак "+",
иначе "-".
Замечание 5.1. Если два уравнения определяют одну и ту же плоскость, то соответствующие коэффициенты их пропорциональны. Действительно, будучи приведены к нормальному виду, оба эти уравнения перейдут в одно и то же нормальное уравнение. Коэффициенты каждого из них пропорциональны коэффициентам этого нормального уравнения, а потому пропорциональны и между собой.
Пример.
5.3.
Уравнение плоскости
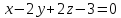 привести к нормальному виду. Нормирующий
множитель будет:
привести к нормальному виду. Нормирующий
множитель будет:
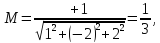
умножая на него данное уравнение, получим:
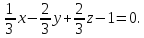
Для данной плоскости, следовательно, имеем:
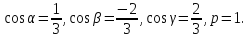
Исследуем теперь, какое положение относительно осей координат занимает плоскость, заданная уравнением
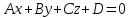 ,
(5.8)
,
(5.8)
если некоторые коэффициенты этого уравнения обращаются в нуль.
Если
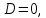 то уравнению (5.8) удовлетворяют
то уравнению (5.8) удовлетворяют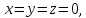 т.е. плоскость проходит через начало
координат. Если
т.е. плоскость проходит через начало
координат. Если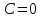 ,
то
,
то
 (5.9)
(5.9)
На
плоскости Oxy это уравнение задает прямую.
Рассматривая же его в пространстве, мы
будем иметь геометрическое место тех
точек, которые проектируются на плоскость
Oxy в точки указанной прямой. Таким
образом, уравнение (5.9) определяет
плоскость, параллельную оси Oz. Аналогично,
если
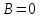 ,
то уравнение
,
то уравнение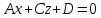 определяет плоскость, параллельную
оси Oy. Наконец, если
определяет плоскость, параллельную
оси Oy. Наконец, если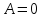 ,
то уравнение
,
то уравнение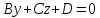 определяет плоскость, параллельную оси
Ox.
определяет плоскость, параллельную оси
Ox.
Допустим
теперь, что два коэффициента равны
нулю,например
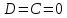 .
Уравнение
.
Уравнение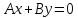 определяет плоскость, проходящую через
начало координат параллельно оси Oz,
т.е. это будет плоскость, проходящая
через ось Oz. Аналогично уравнение вида
определяет плоскость, проходящую через
начало координат параллельно оси Oz,
т.е. это будет плоскость, проходящая
через ось Oz. Аналогично уравнение вида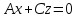 определяет плоскость, проходящую через
ось Oy, а уравнение
определяет плоскость, проходящую через
ось Oy, а уравнение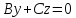 определяет
плоскость, проходящую через ось Ox.
определяет
плоскость, проходящую через ось Ox.
Если
равны нулю два коэффициента при текущих
координатах, например
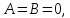 то уравнение
то уравнение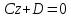 определяет плоскость, параллельную оси
Ox и оси Oy, т.е. плоскость, параллельную
плоскости координат Oxy. Также уравнения
определяет плоскость, параллельную оси
Ox и оси Oy, т.е. плоскость, параллельную
плоскости координат Oxy. Также уравнения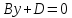 и
и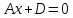 определяют плоскости, параллельные
соответственно Oxz и Oyz.
определяют плоскости, параллельные
соответственно Oxz и Oyz.
Если,
наконец, три коэффициента равны нулю,
например
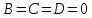 ,
то уравнение
,
то уравнение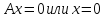 определяет
плоскость координат Oyz. Также уравнения
определяет
плоскость координат Oyz. Также уравнения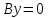 и
и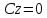 определяют соответственно плоскости
координат Oxz и Oxy.
определяют соответственно плоскости
координат Oxz и Oxy.
Приведем еще несколько форм задания уравнения плоскости.
Уравнение плоскости в отрезках. Рассмотрим плоскость, пересекающую все три координатные оси и не проходящую через начало координат. Ее уравнение можно записать в виде
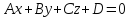 ,
(5.10)
,
(5.10)
где
ни один из коэффициентов
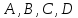 не равен нулю. Обозначим через
не равен нулю. Обозначим через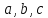 величины отрезков, отсекаемых плоскостью
на осях координат (рис.5.3). Так как точка
величины отрезков, отсекаемых плоскостью
на осях координат (рис.5.3). Так как точка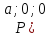 )
лежит на плоскости, то ее координаты
удовлетворяют уравнению (5.10), тогда
)
лежит на плоскости, то ее координаты
удовлетворяют уравнению (5.10), тогда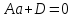 или
или
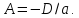
Аналогично,
используя точки
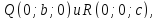 получим:
получим:
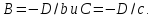
Подставляя
найденные значения
 в уравнение (5.10), получим:
в уравнение (5.10), получим:
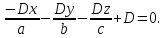
Сокращая
на
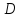 ,
которое в силу предположения не равно
нулю, найдем:
,
которое в силу предположения не равно
нулю, найдем: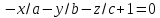 ,
или
,
или
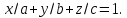
Это и есть искомое уравнение плоскости в отрезках.
Пример
5.4.
Уравнение плоскости
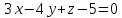 написать в отрезках. Полагая в данном
уравнении
написать в отрезках. Полагая в данном
уравнении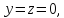 найдем
найдем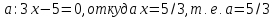 .
Аналогично, полагая
.
Аналогично, полагая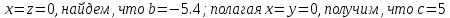 .
Следовательно, искомое уравнение в
отрезах будет
.
Следовательно, искомое уравнение в
отрезах будет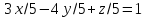 .
.
Уравнение
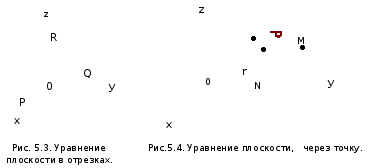
плоскости, проходящей через точку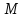 .
Найдем уравнение плоскости, проходящей
через точку
M с
радиус-вектором
.
Найдем уравнение плоскости, проходящей
через точку
M с
радиус-вектором
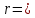 (a;b;c)и
перпендикулярной вектору
(a;b;c)и
перпендикулярной вектору
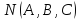 .
Обозначим эту плоскость
.
Обозначим эту плоскость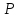 (рис.5.4).
(рис.5.4).
Проведем
радиус-вектор 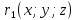 в произвольную точку
в произвольную точку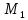 этой плоскости. Тогда вектор
этой плоскости. Тогда вектор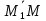 или
или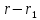 ,
как лежащий в плоскости P, будет
перпендикулярен векторуN.
Поэтому их скалярное произведение равно
нулю:
,
как лежащий в плоскости P, будет
перпендикулярен векторуN.
Поэтому их скалярное произведение равно
нулю:
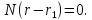 (5.11)
(5.11)
Это
равенство есть условие того, что точка
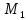 лежит в плоскости
лежит в плоскости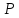 .
Оно справедливо для всех точек этой
плоскости и нарушается только тогда,
когда точка
.
Оно справедливо для всех точек этой
плоскости и нарушается только тогда,
когда точка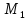 оказывается вне плоскости
оказывается вне плоскости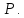 Выражая скалярное произведение векторов
через координаты сомножителей, получим
уравнение плоскости, проходящей
через заданную точку, в координатной
форме:
Выражая скалярное произведение векторов
через координаты сомножителей, получим
уравнение плоскости, проходящей
через заданную точку, в координатной
форме:
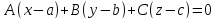 .
(5.12)
.
(5.12)
Изменяя
значения
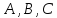 ,
мы будем получать различные плоскости,
проходящие через данную точку
,
мы будем получать различные плоскости,
проходящие через данную точку .
Таким образом, уравнение (5.12) при любых
значениях коэффициентов
.
Таким образом, уравнение (5.12) при любых
значениях коэффициентов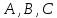 задает плоскость, проходящую через
точку
задает плоскость, проходящую через
точку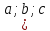 ).
).
Пример
5.5.
Составить уравнение плоскости,
проходящей через точку
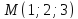 перпендикулярно данному вектору
перпендикулярно данному вектору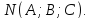 Уравнение искомой плоскости:
Уравнение искомой плоскости:
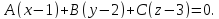
Уравнение
плоскости, проходящей через три заданные
точки, не лежащие на одной прямой.
Рассмотрим три точки, не лежащие на
одной прямой. Обозначим их радиусы-векторы
через 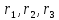 а радиус-вектор текущей точки
а радиус-вектор текущей точки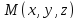 через
через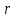 .
Векторы
.
Векторы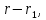
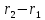 ,
,
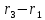 лежат в одной плоскости, следовательно,
они компланарные и их смешанное
произведение равно нулю:
лежат в одной плоскости, следовательно,
они компланарные и их смешанное
произведение равно нулю:
( 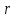 -
-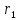 )(
)(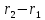 )(
)(
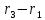 )=0.
(5.13)
)=0.
(5.13)
Это и есть уравнение плоскости, проходящей через три заданные точки в векторной форме. Переходя к координатам, получаем:
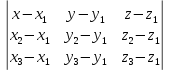 =0
=0
где
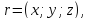
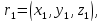
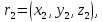
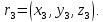
Если
три данные точки лежат на одной прямой,
то векторы
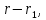
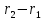 ,
,
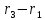 коллинеарны. Поэтому соответствующие
элементы двух нижних строк определителя
пропорциональны и определитель равен
нулю. Следовательно, уравнение (5.14)
обращается в тождество при любых
значениях
коллинеарны. Поэтому соответствующие
элементы двух нижних строк определителя
пропорциональны и определитель равен
нулю. Следовательно, уравнение (5.14)
обращается в тождество при любых
значениях
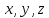 .
Геометрически это означает, что через
каждую точку пространства проходит
плоскость, в которой лежат три данные
точки.
.
Геометрически это означает, что через
каждую точку пространства проходит
плоскость, в которой лежат три данные
точки.
Пример
5.6.
Найти уравнение плоскости, проходящей
через точки

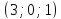 .
Используем уравнение (5.14):
.
Используем уравнение (5.14):
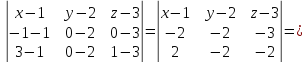
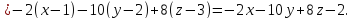
Отсюда
получаем искомое уравнение:
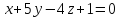 .
.
