
- •2010 Г.
- •Глава 1. Элементы математической логики и теории
- •Глава 2. Элементы линейной алгебры
- •Глава 3. Векторная алгебра
- •Глава 4. Аналитическая геометрия на плоскости
- •Глава 5. Аналитическая геометрия в пространстве
- •Глава 1. Элементы математической логики и теории множеств
- •1.1. Аксиоматический метод
- •1.2. Алгебра высказываний
- •1.3. Логика предикатов
- •1.4. Множества и их элементы
- •1.5. Операции над множествами
- •1.6. Отображения множеств
- •1.7. Мощность множества
- •Глава 2. Элементы линейной алгебры
- •2.1. Системы линейных уравнений
- •2.2. Матрицы и действия над ними
- •2.3. Запись систем в матричной форме и их решение
- •2.4. Определители и их свойства
- •2.5. Правило Крамера
- •2.6. Решение системы линейных уравнений снеизвестными методом Гаусса
- •2.7. Теорема Кронекера-Капелли
- •2.8. Обратная матрица
- •2.9. Векторное пространство
- •Глава 3. Векторная алгебра
- •3.1. Система координат на прямой, на плоскости и в пространстве
- •3.2. Векторы и линейные операции над ними
- •3.3. Скалярное произведение векторов
- •3.4. Векторное произведение двух векторов
- •3.5. Смешанное произведение трех векторов
- •Глава 4. Аналитическая геометрия на плоскости
- •4.1. Уравнение линии в заданной системе координат
- •4.2. Различные формы уравнения прямой на плоскости
- •4.3. Основные задачи на прямую на плоскости
- •4.4. Окружность
- •4.5. Эллипс
- •4.6. Гипербола
- •4.7. Парабола
- •4.8. Классификация кривых второго порядка
- •4.9. Построение эллипса, гиперболы, параболы
- •4.10. Кривые второй степени и конические сечения
- •Глава 5. Аналитическая геометрия в пространстве
- •5.1. Поверхности и линии в пространстве
- •5.2. Уравнение плоскости в пространстве
- •5.3. Основные задачи о положении плоскости
- •5.4. Уравнения прямой в пространстве
- •5.5. Основные задачи о положении прямой
- •5.6. Задачи на взаимное расположение прямой и плоскости
- •5.7. Цилиндрические и конические поверхности
- •5.8. Поверхности вращения
- •5.9. Технические приложения геометрических свойств поверхности
2.7. Теорема Кронекера-Капелли
Вопрос о совместности системы линейных уравнений полностью решается теоремой Кронекера-Капелли, но для ее формулировки нам потребуется новое понятие - ранг матрицы.
Пусть дана матрица

Выберем
в ней произвольные
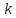 строк и
строк и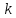 столбцов. Элементы, стоящие на
пересечении этих строк и столбцов,
образуют квадратную матрицу порядка
столбцов. Элементы, стоящие на
пересечении этих строк и столбцов,
образуют квадратную матрицу порядка ,
определитель которой называетсяминором
,
определитель которой называетсяминором
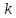 -го
порядка матрицы
-го
порядка матрицы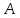 .
Нас будут интересовать порядки тех
миноров, которые отличны от нуля, а
именно наибольший по размерам из этих
миноров. При этом полезно учитывать
следующее замечание, если все миноры
.
Нас будут интересовать порядки тех
миноров, которые отличны от нуля, а
именно наибольший по размерам из этих
миноров. При этом полезно учитывать
следующее замечание, если все миноры
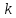 -го
порядка матрица
-го
порядка матрица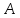 равны нулю, то равны нулю и все миноры
большего порядка.
равны нулю, то равны нулю и все миноры
большего порядка.
Наибольший порядок отличных от нуля миноров называется рангом матрицы.
Рассмотрим
систему линейных уравнений (2.26).
Составим для нее расширенную матрицу
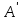 :
:

Теорема 2.2. (Кронекера-Капелли). Система линейных уравнений (2.26) тогда и только тогда совместна, когда ранг расширенной матрицы равен рангу матрицы коэффициентов системы (2.26).
Эта теорема полностью отвечает на вопрос о совместности системы. Вопрос же о количестве решений совместной системы линейных уравнений решается следующим утверждением:
совместная
система (2.26) тогда и только тогда имеет
единственное решение, когда ранг матрицы
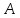 равен числу неизвестных.
равен числу неизвестных.
2.8. Обратная матрица
Ранее мы видели, что найти решение системы можно, используя обратную матрицу. Обратные матрицы нужны так же и при решении матричных уравнений, имеющих вид:
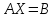 ,
,
где
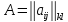 ,
,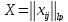 ,
,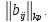
Изложим два способа вычисления обратной матрицы: первый из них даст ответ на вопрос о существовании обратной матрицы, второй является более эффективным с точки зрения вычислений.
Рассмотрим
квадратную матрицу
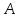 ,
имеющую порядок
,
имеющую порядок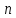
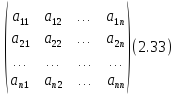
Союзной
по отношению к матрице
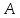 называется матрица
называется матрица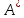 ,
которая строится следующим образом:
сначала каждый элемент матрицы
,
которая строится следующим образом:
сначала каждый элемент матрицы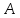 заменяется его алгебраическим дополнением,
а затем полученная матрица транспонируется.
заменяется его алгебраическим дополнением,
а затем полученная матрица транспонируется.
Теорема
2.3. Квадратная
матрица 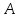 тогда и только тогда имеет обратную,
когда ее определитель не равен нулю
(
тогда и только тогда имеет обратную,
когда ее определитель не равен нулю
(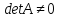 ),
при этом
),
при этом
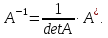
1
Доказательство. Проведем его на примере матрицы третьего порядка. Покажем, что
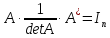 .
.
Имеем:

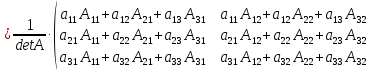
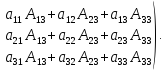
Элементы
последней матрицы, не лежащие на главной
диагонали, являются суммами произведений
элементов какой-то строки матрицы
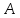 на алгебраические дополнения элементов
какой-то другой ее строки. Ранее было
показано, что такие суммы равны нулю.
Диагональные же элементы являются
разложением определителя матрицы
на алгебраические дополнения элементов
какой-то другой ее строки. Ранее было
показано, что такие суммы равны нулю.
Диагональные же элементы являются
разложением определителя матрицы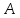 по элементам соответствующей строки,
а потому они равны определителю матрицы
по элементам соответствующей строки,
а потому они равны определителю матрицы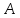 .
Деля эту матрицу на
.
Деля эту матрицу на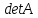 (а делить можно тогда и только тогда,
когда
(а делить можно тогда и только тогда,
когда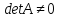 )
получим единичную матрицу. Так как
союзная матрица отличается от обратной
только множителем, то из существования
обратной матрицы следует и существование
союзной и, следовательно, в этом случае
)
получим единичную матрицу. Так как
союзная матрица отличается от обратной
только множителем, то из существования
обратной матрицы следует и существование
союзной и, следовательно, в этом случае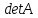
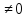 .
Теорема доказана.
.
Теорема доказана.
Пример
2.11.
Найти матрицу, обратную к матрице
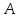 ,
если
,
если
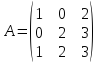 .
.
Решение.
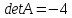 ,
следовательно обратная матрица
существует. Вычислим алгебраические
дополнения:
,
следовательно обратная матрица
существует. Вычислим алгебраические
дополнения:
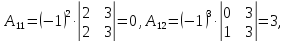
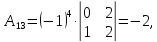
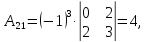
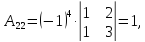
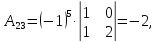
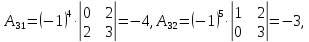
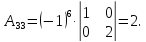
Тогда союзной будет матрица
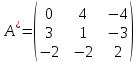 ,
,
а обратной – матрица

Для проверки правильности вычислений можно полученную матрицу умножить на исходную. Мы оставляем это читателю.
Рассмотрим другой метод вычисления обратной матрицы, использующий преобразования, применявшиеся нами при вычислении определителей и при решении систем линейных уравнений. Итак, вычислим обратную матрицу, используя схему метода Гаусса.
Для
вычисления матрицы, обратной матрице
(2.33), рассмотрим матрицу 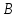 ,
состоящую из двух частей, одна из
которых это матрица
,
состоящую из двух частей, одна из
которых это матрица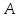 а другая - единичная матрица того же
порядка:
а другая - единичная матрица того же
порядка:

Теперь,
используя схему последовательных
исключений Гаусса, преобразуем матрицу
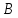 так, чтобы в левой ее части получилась
единичная матрица, тогда в правой части
будет стоять матрица, обратная к
так, чтобы в левой ее части получилась
единичная матрица, тогда в правой части
будет стоять матрица, обратная к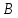 .
Преобразовывая матрицу
.
Преобразовывая матрицу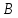 ,
мы можем умножать все элементы строки
матрицы
,
мы можем умножать все элементы строки
матрицы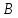 на одно и то же число и складывать
соответствующие элементы двух строк.
на одно и то же число и складывать
соответствующие элементы двух строк.
Строку
матрицы
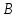 ,
умноженную каждый раз на свое конкретное
число, будем складывать с каждой другой
строкой (кроме нее самой) матрицы
,
умноженную каждый раз на свое конкретное
число, будем складывать с каждой другой
строкой (кроме нее самой) матрицы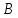 .
Так поступим с каждой строкой матрицы
.
Так поступим с каждой строкой матрицы .
.
Мы оставляем не доказанным тот факт, что изложенный алгоритм действительно даст обратную матрицу, заметим только, что этот факт следует из свойств операции умножения матриц.
Пример 2.12. Найти матрицу, обратную к матрице

Матрица
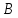 будет иметь вид:
будет иметь вид:

Умножим
элементы первой строки матрицы
 на (-89/102) и
прибавим получившиеся значения к
соответствующим элементам второй
строки; затем умножим первую строку
матрицы
на (-89/102) и
прибавим получившиеся значения к
соответствующим элементам второй
строки; затем умножим первую строку
матрицы на (-449/102) и
сложим с третьей строкой. Первую строку
разделим на 102. В результате матрица
на (-449/102) и
сложим с третьей строкой. Первую строку
разделим на 102. В результате матрица превратится
в матрицу
превратится
в матрицу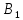 :
:

Умножим
элементы второй строки матрицы
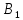 на (-0.87255/4.34314) и прибавим их к
соответствующим элементам первой
строки; затем вторую строку из
на (-0.87255/4.34314) и прибавим их к
соответствующим элементам первой
строки; затем вторую строку из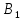 умножим на (-9.22550/4.34314) и сложим с
третьей её строкой. Вторую строку
матрицы
умножим на (-9.22550/4.34314) и сложим с
третьей её строкой. Вторую строку
матрицы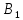 разделим на 4.34314, получим матрицу
разделим на 4.34314, получим матрицу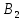 :
:

Умножим
третью строку из
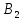 на (-2.54853/4.92331) и сложим с первой её
строкой. Умножим третью строку на
(-2.12415/4.92331) и сложим со второй. Разделим
третью строку на 4.92331, получим матрицу
на (-2.54853/4.92331) и сложим с первой её
строкой. Умножим третью строку на
(-2.12415/4.92331) и сложим со второй. Разделим
третью строку на 4.92331, получим матрицу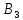 :
:

После округлении до тысячных получаем:

