4.4. Зависимость между непрерывностью и дифференцируемостью функции

Сформулируем необходимое условие существования производной.

Теорема.

Если функция дифференцируема в некоторой точке, то в этой точке функция непрерывна.

Заметим, что обратное утверждение неверно: непрерывная функция может не иметь производной.

Например, функция непрерывна при, но не дифференцируема для этого значения, так как в точкеграфика функциине существует касательной.

Таким образом, непрерывность функции необходимое, но не достаточное условие дифференцируемости функции.

4.4. Производная суммы, разности, произведения и частного функций

Нахождение производной функции непосредственно по определению (п.4.1) часто связано с определенными трудностями. На практике функции дифференцируют с помощью ряда правил и формул.

Теорема.

Если функции идифференцируемы в точкех, то в этой точке дифференцируемы функции ,,(при условии, что) и при этом

;

;

, .

Следствия

1. , где.

2. Если , то.

3. , где.

4.6. Производная сложной функции

Пусть и, тогда− сложная функция с промежуточным аргументомu и независимым аргументом х.

Теорема.

Если функции имеет производную в точке х, а функция имеет производнуюв соответствующей точке, то сложная функцияв точкех имеет производную , которая находится по формуле:

или =.

Кратко это можно сформулировать так (правило цепочки): производная сложной функции равна произведению производных от функций ее составляющих.

Данное правило распространяется на сложные функции при любом (определенном) числе промежуточных аргументов.

Так, если ,,,, то

.

4.7. Производная обратной функции

Если и− взаимо-обратные дифференцируемые функции и, то

или ,

т.е. производная обратной функции равна обратной величине производной данной функции.

Записывают:

или .

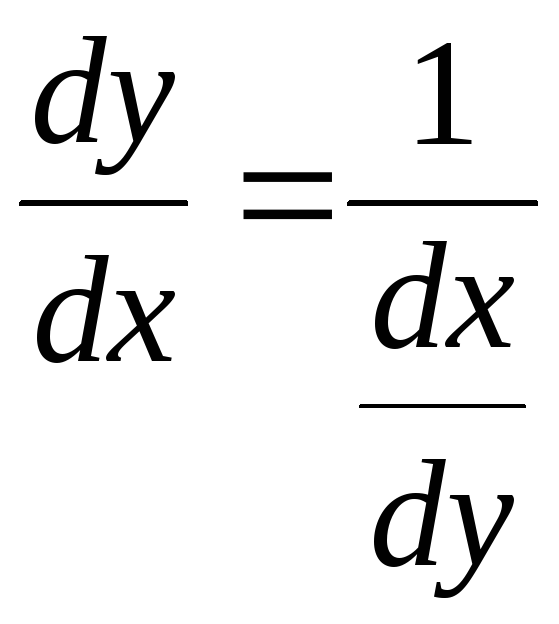Пример

Найти производную функции .

, , тогда,. Имеем.

.

Итак, .

4.8. Таблица производных

Для удобства и упрощения процесса дифференцирования формулы производных основных элементарных функций и правила дифференцирования сведены в таблицу.

Правила дифференцирования		Формулы дифференцирования
1.		1.	,
2.		2.
3.	,	3.
4.	, .	4.
5.	,	5.
6.	, если ,	6.
7.	, если ,	7.
		8.
		9.
		10.
		11.
		12.
		13.
		14.
		15.
		16.
		17.

4.9. Примеры отыскания производных сложных функций

На практике чаще всего приходится находить производные от сложных функций. Покажем на примерах, как находить производные от таких функций.

1. ,k − число.

;

.

2. .

;

.

3. .

;

.

4. .

;

.

5. .

;

.

6. .

;

;

.

7. .

.

8. .

;

.

9. .

.

10. .

;

.

Для случая дифференцирования сложных функций, таблицу производных можно переписать в более общем виде.

Формулы дифференцирования основных элементарных функций от промежуточного аргумента ()

1.		2.
3.		4.
5.		6.
7.		8.
9.		10.
11.		12.
13.		14.

4.10. Производная функции, заданной параметрически

Зависимость между переменными х и y может быть задана параметрически в виде двух уравнений:

где t − вспомогательная переменная (параметр).

Функцию , определяемую этими уравнениями, можно рассматривать как сложную функцию, где.

По правилу дифференцирования сложной функции имеем:

.

Так как , то

.

Примеры

Найти производные функций:

1.

.

2.

.

4.11 Производная неявной функции

Если неявная функция задана уравнением , то для нахождения производной оту по х надо продифференцировать это уравнение по х, рассматривая при этом у как функцию от х, и затем, полученное уравнение разрешить относительно , выразивчерезх и у.

Пример

Найти производную функции: .

;

;

;

.

4.12. Логарифмическое дифференцирование

В ряде случаев, когда приходится дифференцировать произведение многих сомножителей или частное, в котором и числитель и знаменатель состоят из нескольких сомножителей, а также при нахождении производных от показательно-степенной функции , применяютлогарифмическое дифференцирование.

Метод логарифмического дифференцирования заключается в том, что от заданной функции у сначала находится натуральный логарифм, а затем результат дифференцируется:

.

Из полученного равенства определяется :

.

Примеры

Найти производные функций:

1. .

;

;

;

;

.

2. .

;

;

;

.

4.13. Производные высших порядков

Производная от функцииназываетсяпроизводной первого порядка (или первой производной) и представляет собой функцию от х.

Производную от первой производной называют производной второго порядка или второй производной и обозначают ,,.

Итак, по определению

.

Вторая производная играет роль ускорения изменения функции.

Производная от производной второго порядка называется производной третьего порядка и обозначается ,,.

Таким образом,

.

Производной n-го порядка (или n-й производной) называется производная от производной (n-1) порядка:

.

Число n, указывающее порядок производной, заключают в скобки, чтобы не путать с показателем степени.

Производные порядка выше первого называются производными высших порядков.

Порядок производной, начиная с четвертого, обозначают римскими цифрами или арабскими цифрами в скобках, например, илии т.д.