Глава 3
.doc
ГЛАВА 3
НЕПРЕРЫВНОСТЬ ФУНКЦИИ
3.1. Определение непрерывности функции в точке
С понятием предела функции тесно связано понятие непрерывности функции.
Пусть функция
определена в точке
и в некоторой окрестности этой точки.
Чтобы уяснить понятие непрерывности,
рассмотрим точку
,
в которой функция
непрерывна (рис.3.1).
Рис. 3.1
Из рисунка видно,
что, во-первых, в точке
функция принимает значение
.
Во-вторых, если
,
то
(независимо от того, как
слева или справа).
Таким образом, в
точке
выполняется условие: если
,
то
.
Это условие можно записать так:
.
Определение.
Функция
называется непрерывной
в точке
,
если существует предел функции в этой
точке и он равен значению функции в этой
точке:
|
|
(1) |
Данное равенство означает выполнение трех условий:
-
функция
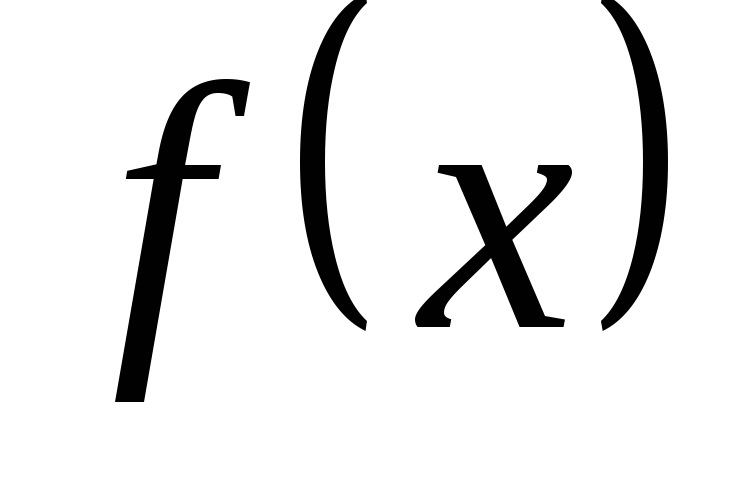определена в точке
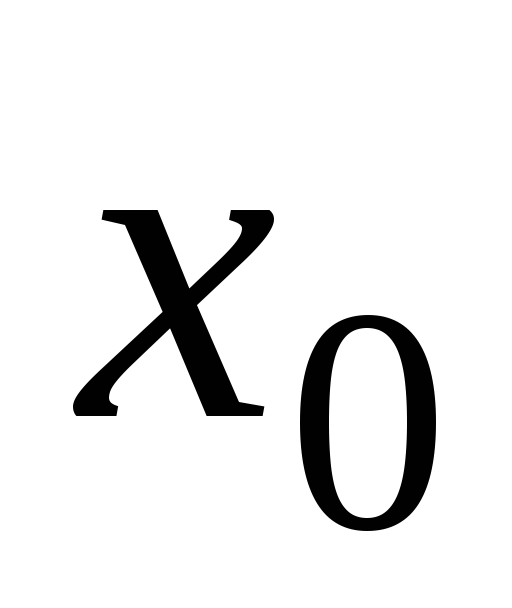и в ее окрестности; -
функция
имеет предел при
; -
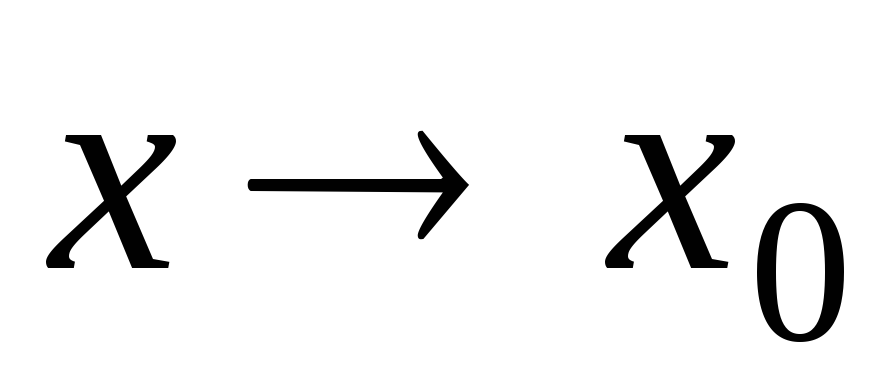предел функции в точке
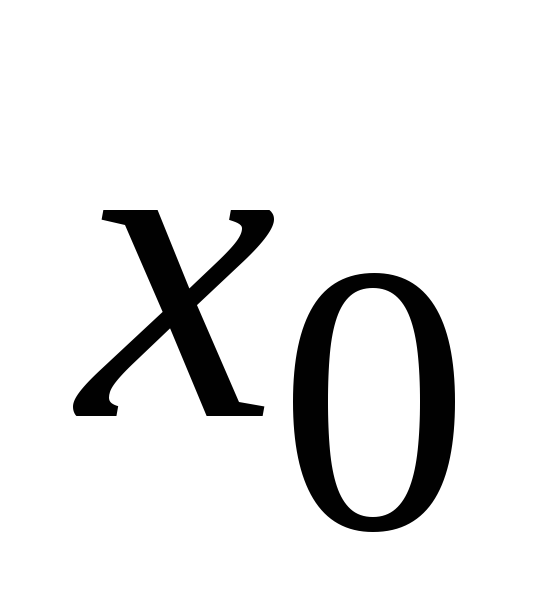равен значению функции в этой точке.
Для того, чтобы
функция
была непрерывна в точке
,
должны быть выполнены все три перечисленные
условия. Нарушение хотя бы одного из
них в некоторой точке означает, что
функция разрывна в этой точке.
Когда
,
то
,
и равенство (1) можно записать в виде
.
Это означает, что
при нахождении предела непрерывной
функции
можно перейти к пределу под знаком
функции, т.е. в функцию
вместо аргумента х
подставить его предельное значение
.
Для некоторых практических применений бывает полезно другое определение непрерывности функции, которое опирается на понятие приращения аргумента и функции (рис. 3.2).
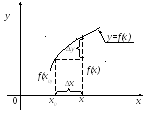
Рис. 3.2
Пусть функция
определена в точке
и в ее окрестности. При
функция принимает значение
,
а при
,
соответственно,
.
Приращение функции равно
.
Если
,
то
,
тогда
.
Следовательно,
Определение.
Функция
называется непрерывной
в точке
,
если бесконечно малому приращению
аргумента соответствует бесконечно
малое приращение функции:
.
Исследуя непрерывность функции в точке применяют, либо первое, либо второе определения.
3.2. Односторонняя непрерывность в точке. Непрерывность функции в интервале и на отрезке
По аналогии с понятием предела функции слева (справа) вводится понятие непрерывности функции слева (справа).
Пусть функция
определена на полуинтервале
,
и в точке
у нее существует предел слева, т.е.
.
Если этот предел равен значению функции
в точке
,
т.е.
или
,
то эту функцию называют непрерывной
слева в точке
.
Аналогично, если
функция
определена на полуинтервале
и
или
,
то эту функцию называют непрерывной
справа в точке
.
Для того, чтобы выполнялось условие непрерывности функции в точке
,
необходимо и достаточно, чтобы функция была непрерывна как слева, так и справа в этой точке.
Пользуясь односторонними пределами, условие непрерывности можно заменить равносильным ему двойным равенством, т.е., поскольку
,
то
.
Таким образом,
функция
непрерывна в точке
,
тогда и только тогда, когда в этой точке
существуют пределы слева и справа, они
равны между собой и равны значению
функции в этой точке.
Определение.
Функция
называется непрерывной
в интервале
,
если она непрерывна в каждой точке этого
интервала.
Определение.
Функция
называется непрерывной
на отрезке
,
если она непрерывна в интервале
,
и в точке
непрерывна
справа, т.е.
,
а в точке
непрерывна
слева, т.е.
.
3.3. Точки разрыва функции и их классификация
Если в точке
функция не определена, или не существует
предел
,
или
при произвольном стремлении
,
то при
функция
разрывна.
Определение.
Точки, в которых нарушается непрерывность функции, называются точками разрыва этой функции.
Точки разрыва функции классифицируются в зависимости от того, как именно нарушено двойное равенство
или 
,
являющееся условием непрерывности функции в точке.
Все точки разрыва функции разделяются на точки разрыва первого и второго рода.
Определение.
Точка разрыва
называется точкой
разрыва первого рода
функции
,
если в этой точке существуют и конечны
пределы функции слева и справа, т.е.
и
.
При этом
1) если
,
то
− точка устранимого разрыва (рис.3.3);
2) если
,
то
− точка конечного разрыва (рис.3.4).
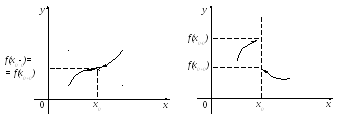
Рис. 3.3 Рис. 3.4
Определение.
Точка разрыва
называется точкой
разрыва второго рода функции
,
если хотя бы один из односторонних
пределов не существует или равен
бесконечности (рис. 3.5).
Рис. 3.5
Примеры
Найти точки разрыва функций и определить их род.
1.
;
Функция определена
при всех значениях х,
кроме
.
Найдем пределы функции слева и справа
в точке
.
;
.
Функция в точке
имеет бесконечный разрыв и
− точка разрыва второго рода.
2.
;
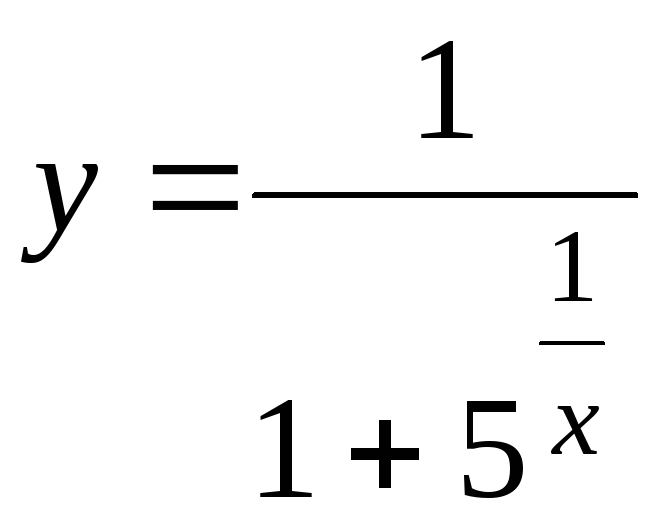Точкой разрыва
для функции является точка
.
Вычислим левый и правый пределы функции
при
.
;
.
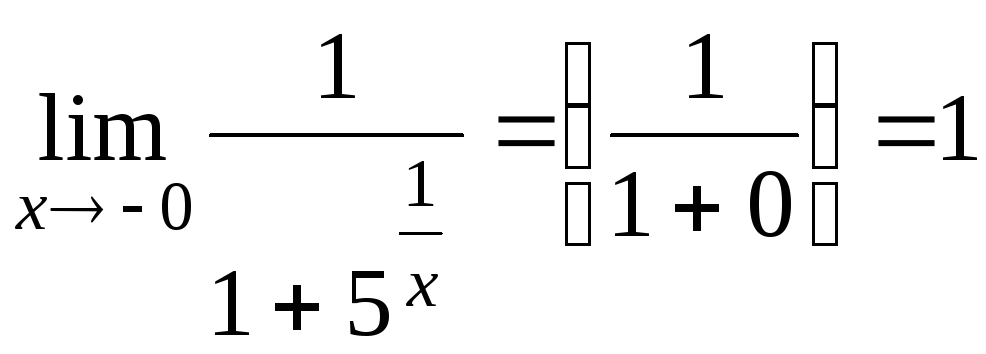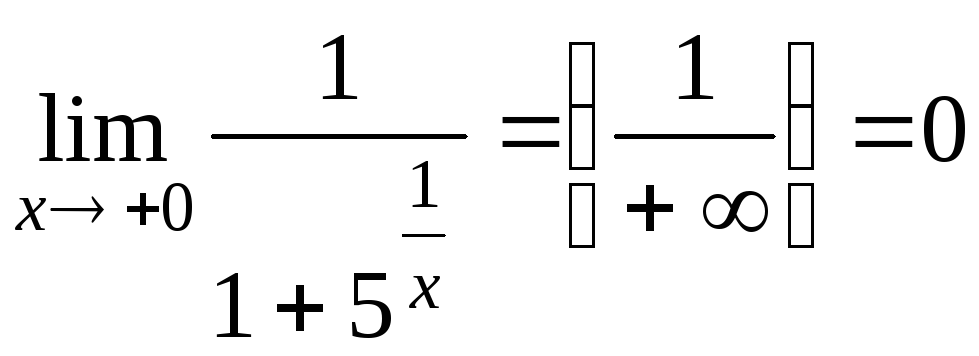Поскольку левый
и правый пределы при
являются конечными, то точка
− точка разрыва первого рода.
3.4. Основные теоремы о непрерывных функциях. Непрерывность элементарных функций
Теоремы о непрерывности функций следуют непосредственно из соответствующих теорем о пределах. Приведем теоремы о непрерывных функциях без доказательств.
Теорема.
Сумма, разность, произведение и частное двух непрерывных функций есть функция непрерывная (для частного − делитель отличен от нуля).
Теорема.
Сложная функция, составленная из конечного числа непрерывных функций, непрерывна.
Теорема.
Функция, обратная
к монотонной и непрерывной на интервале
функции, также монотонна и непрерывна
на интервале
.
Для основных элементарных функций (п.1.7), справедлива следующая теорема.
Теорема.
Всякая основная элементарная функция непрерывна в каждой точке, в которой она определена.
Подавляющее большинство функций, которые рассматриваются в математике, являются элементарными. Опираясь на определение элементарной функции (§1.10), непрерывность основных элементарных функций, а также на приведенные выше теоремы можно утверждать, что всякая элементарная функция непрерывна в ее области определения.
3.5. Свойства функций, непрерывных на отрезке
Рассмотрим некоторые свойства функций, непрерывных на отрезке. Сформулируем эти свойства в виде теорем, не приводя доказательств.
Теорема.
Если функция
непрерывна на отрезке, то она достигает
на этом отрезке своего наибольшего и
наименьшего значений (рис.3.6).
Следствие. Если функция непрерывна на отрезке, то она ограничена на этом отрезке.
Рис. 3.6
Теорема.
Если функция
непрерывна на отрезке
и принимает на его концах неравные
значения
и
,
то на этом отрезке она принимает и все
промежуточные значения между
и
(рис.3.7).
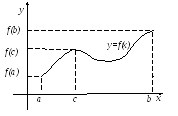
Рис. 3.7
Теорема.
Если функция
непрерывна на отрезке
и на его концах принимает значения
разных знаков, то внутри отрезка
найдется хотя бы одна точка с,
в которой функция
обращается в нуль:
(рис.3.8).
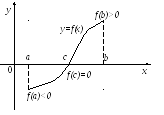
Рис. 3.8
Упражнения
Найти точки разрыва функций и определить их род.
1.
; Ответ:
,
второго рода;
2.
; Ответ:
,
второго рода;
3.
; Ответ:
,
первого рода;
4.
; Ответ:
,
первого рода;
5.
; Ответ:
,
все точки разрыва второго рода.