5.5. Асимптоты графика функции

Построение графика функции значительно облегчается, если знать его асимптоты.

Определение.

Асимптотой кривой называется прямая, расстояние до которой от точки, лежащей на кривой, стремится к нулю при неограниченном удалении от начала координат этой точки по кривой (рис.5.10).

Асимптоты бывают вертикальные (параллельные оси Оу), горизонтальные (параллельные оси Ох) и наклонные.

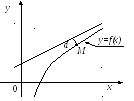
Рис. 5.10

Вертикальные асимптоты

Определение.

Прямая называетсявертикальной асимптотой графика функции , если выполнено одно из условий:

или (рис.5.11)

Рис. 5.11

Вертикальные асимптоты, уравнение которых х=x₀ , следует искать в точках, где функция терпит разрыв второго рода, или на концах ее области определения, если концы не равны . Если таких точек нет, то нет и вертикальных асимптот.

Например, для кривой , вертикальной асимптотой будет прямая, так как,. Вертикальной асимптотой графика функцииявляется прямая(осьОу), поскольку

.

Горизонтальные асимптоты

Определение.

Если при () функцияимеет конечный предел, равный числуb:

,

то прямая есть горизонтальная асимптота графика функции.

Например, для функции имеем

, .

Соответственно, прямая − горизонтальная асимптота для правой ветви графика функции, а прямая− для левой ветви.

В том случае, если

,

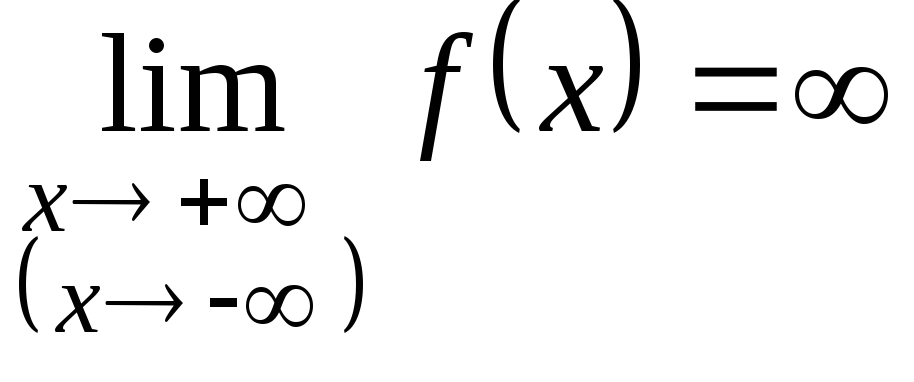график функции не имеет горизонтальных асимптот, но может иметь наклонные.

Наклонные асимптоты

Определение.

Прямая называетсянаклонной асимптотой графика функции при(), если выполняется равенство

.

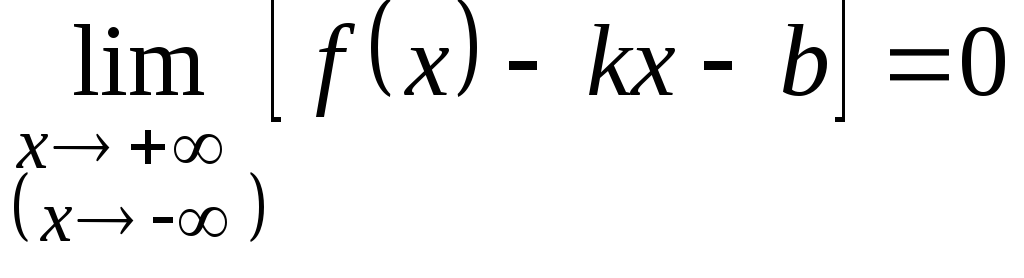Наличие наклонной асимптоты устанавливают с помощью следующей теоремы.

Теорема.

Для того, чтобы график функции имел при() наклонную асимптоту, необходимо и достаточно, чтобы существовали конечные пределы

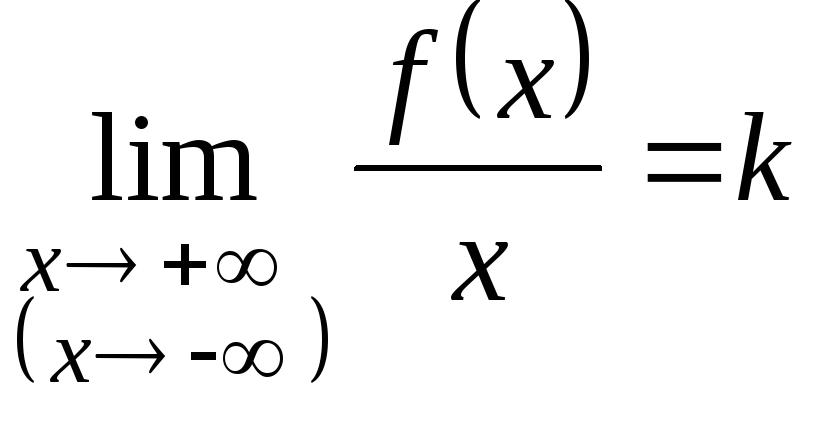и .

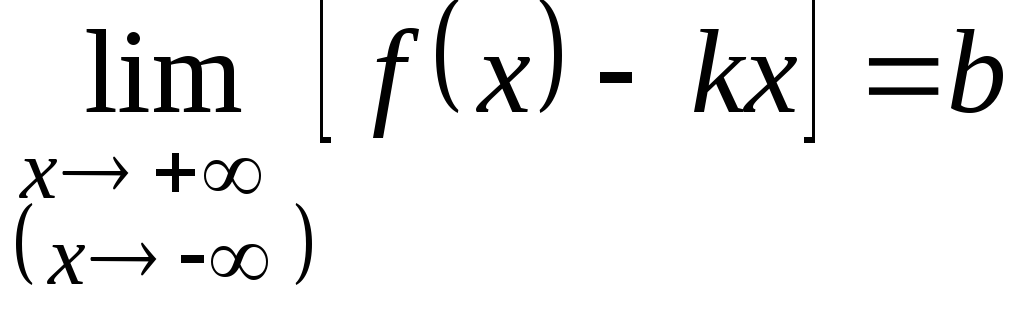Если хотя бы один из этих пределов не существует или равен бесконечности, то кривая наклонной асимптоты не имеет.

Замечания.

1. При отыскании асимптот следует отдельно рассматривать случаи и.

2. Есл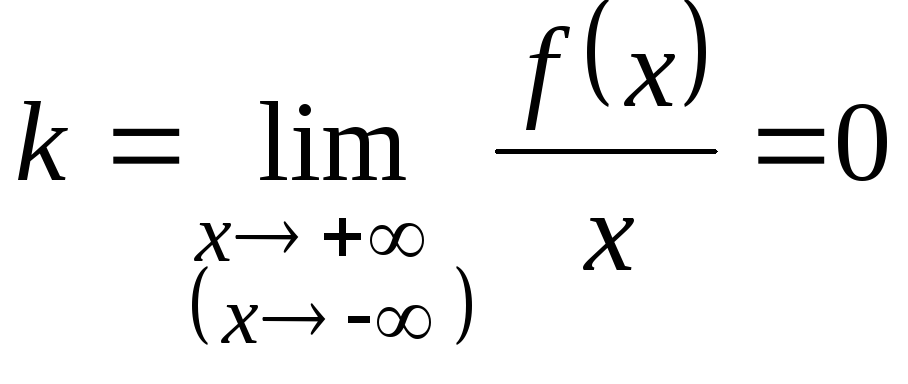и

и ,

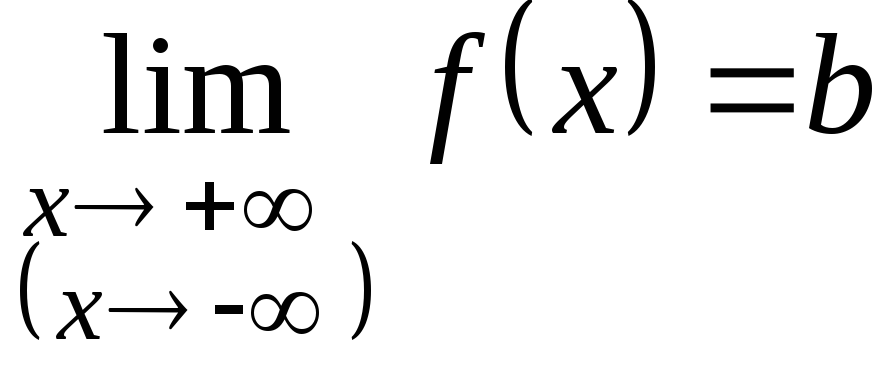то график функции имеет горизонтальную асимптоту.

3. Есл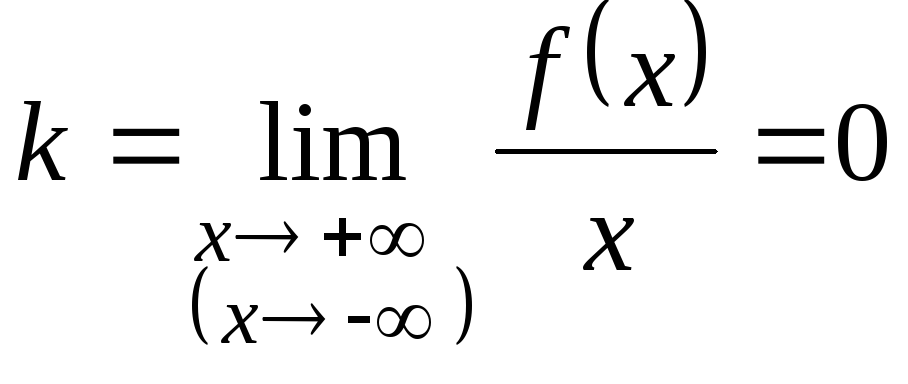и

и ,

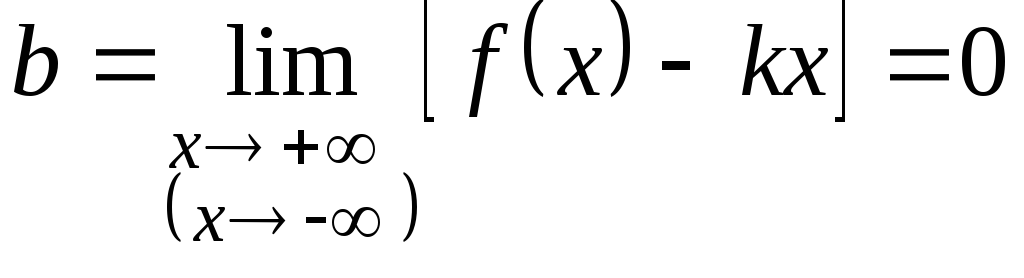то прямая (осьОх) является горизонтальной асимптотой графика функции .

Из замечаний следует, что горизонтальную асимптоту можно рассматривать как частный случай наклонной асимптоты при . Поэтому при отыскании асимптот графика функции рассматривают лишь два случая:

1) вертикальные асимптоты,

2) наклонные асимптоты.

Пример

Найти асимптоты графика функции .

.

1) − точка разрыва второго рода:

, .

Прямая − вертикальная асимптота.

2) ,

,

.

Прямая − горизонтальная асимптота. Наклонной асимптоты нет.

5.6. Общая схема исследования функции и построение графика

В предыдущих параграфах было показано, как с помощью производных двух первых порядков изучаются общие свойства функции. Пользуясь результатами этого изучения, можно составить представление о характере функции и, в частности, построить ее график.

Исследование функции целесообразно проводить по следующей схеме.

1. Найти область определения функции.

2. Исследовать функцию на четность и нечетность.

3. Исследовать функцию на периодичность.

4. Найти точки пересечения графика функции с осями координат.

5. Найти интервалы знакопостоянства функции (интервалы, на которых 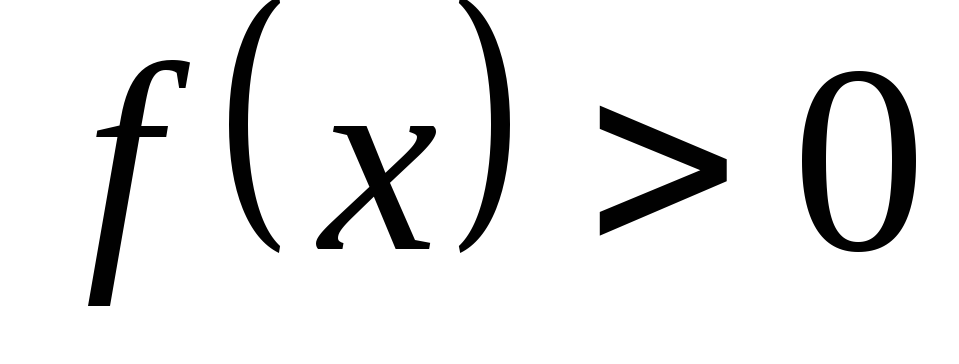или).

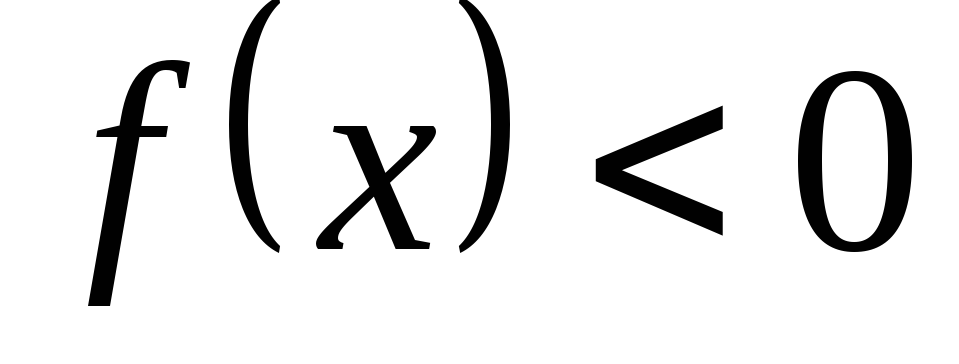6. Найти асимптоты графика функции.

7. Найти интервалы монотонности и точки экстремума функции.

8. Найти интервалы выпуклости и вогнутости и точки перегиба графика функции.

9. Построить график функции.

Пример

Исследовать функцию и построить ее график.

1. Область определения функции .

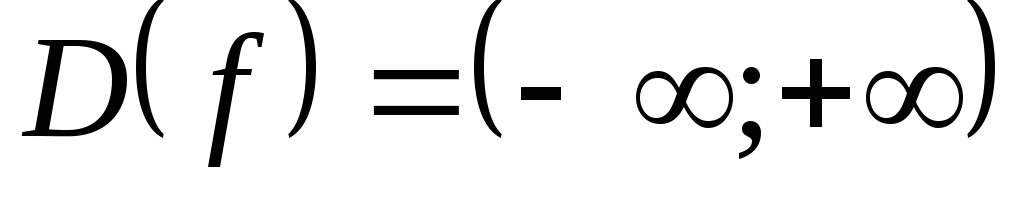2. Функция нечетная: 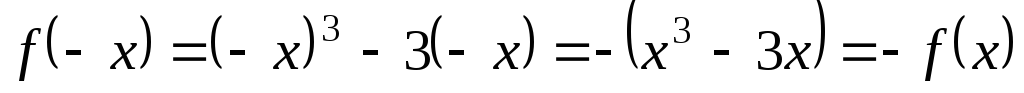. График функции симметричен относительно начала координат

3. Функция непериодическая.

4. Точки пересечения с осями координат:

С осью Оу: , точка.

С осью Ох: ,,,.

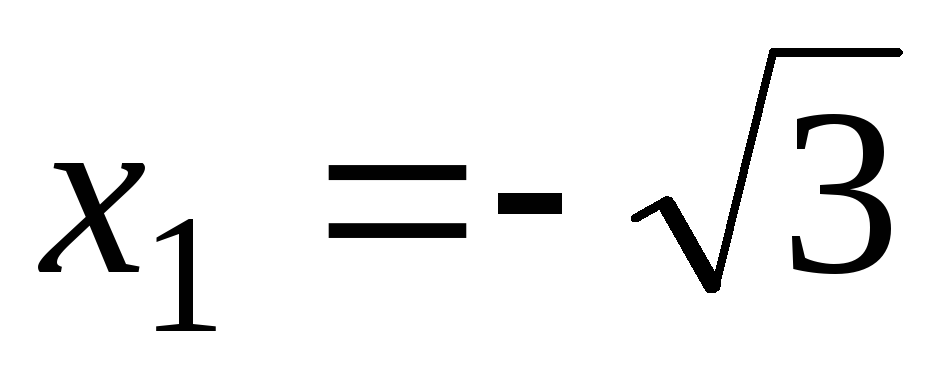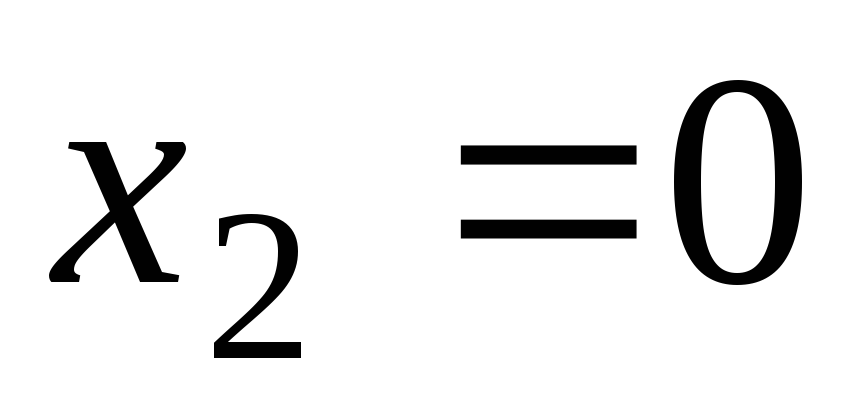5. Точки ,и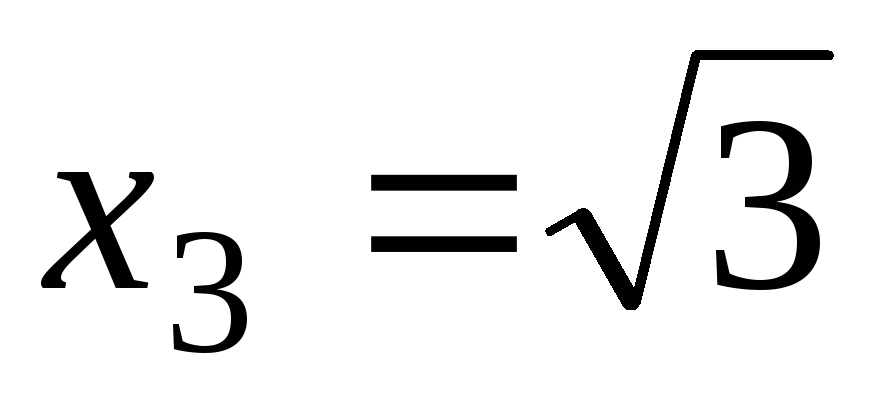разбивают осьОх на четыре интервала.

при ;

при ;

при ;

при .

6. Так как функция является непрерывной, то ее график не имеет вертикальных асимптот.

.

Наклонной и горизонтальной асимптот нет.

7. ,

, ,− критические точки.

для «↑»,

для «↓»,

для «↑».

Сведем данные в таблицу.

х		-1		1
	+	0	−	0	+
	↑ (возрастает)	mах 2	↓ (убывает)	min -2	↑ (возрастает)

, ;

точка − максимум;

точка − минимум.

8. , ,,.

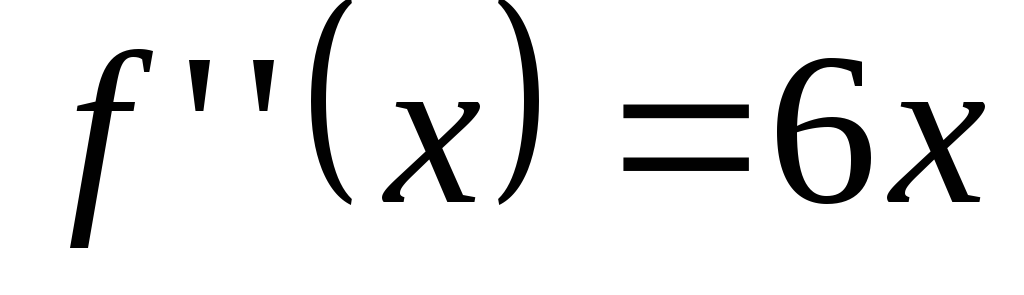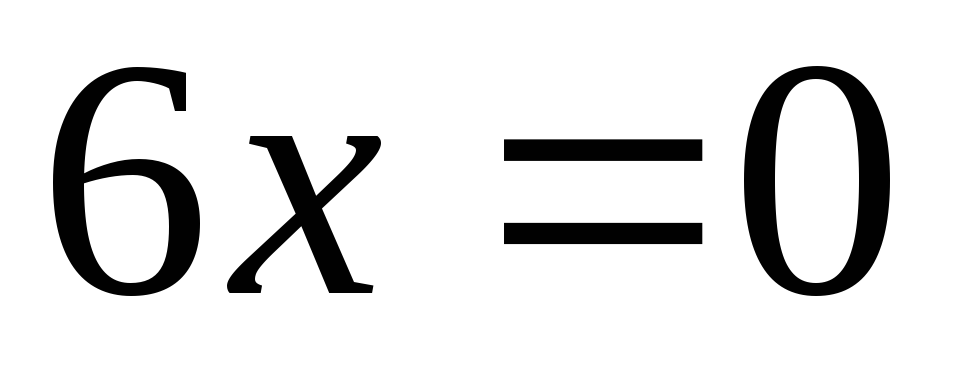при «»;

при «».

х		0
	−	0	+
	(выпуклый)	0 (точка перегиба)	(вогнутый)

Точка − точка перегиба.

9. График функции 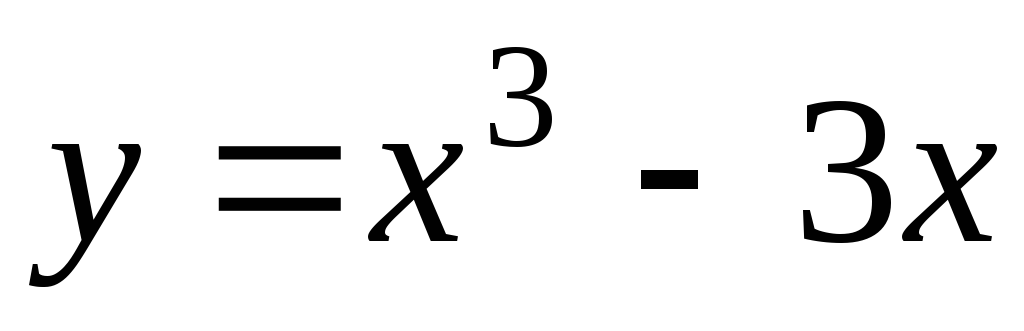(рис.5.12)

Рис. 5.12