
- •Глава 6 неопределенный интеграл
- •6.1. Первообразная функция
- •Примеры
- •6.2. Неопределенный интеграл
- •6.3. Свойства неопределенного интеграла
- •6.4. Таблица основных интегралов
- •6.5. Методы интегрирования
- •Примеры
- •Подстановка вида
- •Примеры
- •Метод интегрирования по частям
- •Примеры
- •Упражнения
- •Литература
- •Оглавление
Примеры
1.
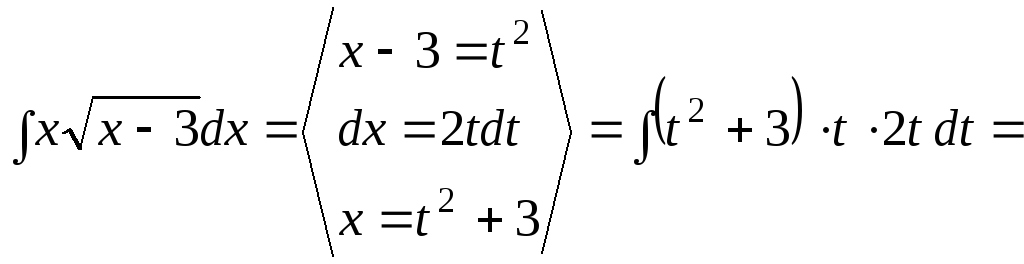
![]()
2.
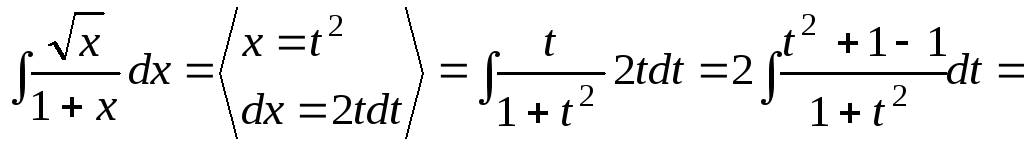
![]()
![]() .
.
Метод интегрирования по частям
Метод интегрирования по частям следует из формулы дифференцирования произведения двух функций.
Если
![]() и
и![]() − дифференцируемые функции, то
− дифференцируемые функции, то
![]() .
.
Интегрируя это равенство, получим
![]()
или
![]() .
.
Тогда
![]() .
.
Последняя формула
называется формулой
интегрирования по частям.
Она сводит вычисление интеграла
![]() к вычислению интеграла
к вычислению интеграла![]() ,
который может оказаться более простым,
чем первый.
,
который может оказаться более простым,
чем первый.
В таблице приведены типы интегралов, которые могут быть вычислены только по частям, и указано, что следует принимать за u и, что на dv.
|
№ п/п |
Интеграл |
u |
dv |
|
1. |
|
|
|
|
2. |
|
|
|
|
3. |
|
|
|
|
4. |
|
|
|
|
5. |
|
|
|
|
6. |
|
|
|
|
7. |
|
|
|
|
8. |
|
|
|
|
9. |
|
|
|
|
10. |
|
|
|
где а и b − числа.
Замечание.
Иногда, для получения результата надо последовательно применить интегрирование по частям несколько раз.
Примеры
1.
![]() ;
;
2.
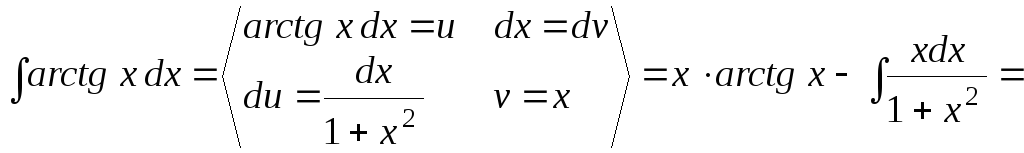
![]() ;
;
3.
![]()
![]()
![]() .
.
Упражнения
Найти интегралы, используя непосредственное интегрирование:
|
1. |
|
Ответ:
|
|
2. |
|
Ответ:
|
|
3. |
|
Ответ:
|
|
4. |
|
Ответ:
|
|
5. |
|
Ответ:
|
|
6. |
|
Ответ:
|
|
7. |
|
Ответ:
|
|
8. |
|
Ответ:
|
|
9. |
|
Ответ:
|
|
10. |
|
Ответ:
|
Найти интегралы, используя метод подстановки:
|
11. |
|
Ответ:
|
|
12. |
|
Ответ:
|
|
13. |
|
Ответ:
|
|
14. |
|
Ответ:
|
|
15. |
|
Ответ:
|
|
16. |
|
Ответ:
|
|
17. |
|
Ответ:
|
|
18. |
|
Ответ:
|
|
19. |
|
Ответ:
|
|
20. |
|
Ответ:
|
|
21. |
|
Ответ:
|
|
22. |
|
Ответ:
|
|
23. |
|
Ответ:
|
|
24. |
|
Ответ:
|
Найти интегралы, используя интегрирование по частям:
|
25. |
|
Ответ:
|
|
26. |
|
Ответ:
|
|
27. |
|
Ответ:
|
|
28. |
|
Ответ:
|
|
29. |
|
Ответ:
|
|
30. |
|
Ответ:
|
Литература
1. Ахтямов А.М. Математика для социологов и экономистов.− М.: Физматлит, 2004.
2. Ганичева А.В., Козлов В.П. Математика для психологов.−М.: Аспект Пресс, 2005.
3. Демидович Б.П., Кудрявцев В.А. Краткий курс высшей математики.− М.: АстрельАСТ, 2004.
4. Дорофеева А.В. Высшая математика. Гуманитарные специальности.− М.: Дрофа, 2004.
5. Лунгу К.Н., Письменный Д.Т., Федин С.Н., Шевченко Ю.А. Сборник задач по высшей математике.−М.: Айрис Пресс, 2006.
6. Натансон И.П. Краткий курс высшей математики. −М.: Наука, 1968.
7. Тер-Крикоров А.М., Шабунин М.И. Курс математического анализа.− М.: Физматлит, 2003.
8. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. Т.I,II.−М.: Наука, 1966.
9. Фролов С.В., Шостак Р.Я. Курс высшей математики.−М.: Высшая школа, 1973.
