met_ teor_wer_i_mat_st

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Таврический государственный агротехнологический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

M (X )= òx × 2xdx = 2ò x2 dx =

.pdf

Скачиваний:

Добавлен:

02.03.2016

Размер:

618.53 Кб

Скачать

☆

<<< < Предыдущая 12 / 42 3 4 > Следующая >>>

ì0

при x £ 1

F (x)

при 1

< x

£ 4

ï0,3

F (x )= íï0,5 при 4 < x £ 5 .

1,0

ï0,9 при 5 < x

£ 7

> 7

ï1, 0 при x

Зобразимо функцію

F (x)

графічно (рис. 5).

0,5

Функція

розподілу

0,3

любої

дискретної

випад-

кової величини є розривна

ступенева функція, стриб-

ки якої

проходять

в точ-

ках, що відповідають мо-

1 2

3 4 5 6 7

жливим

значенням випад-

кової

величини

рівні

ймовірностям цих значень.

Рис. 5

Сума усіх стрибків функ-

ції F (x)

дорівнює одиниці.

Властивості функції розподілу

1.Функція розподілу випадкової величини є невід’ємна функція, заключна між нулем і одиницею 0 £ F (x) £ 1 .

2.Функція розподілу випадкової величини є не спадаюча функція на усій числовій осі.

3.На мінус нескінченності функція розподілу дорівнює нулю, на плюс нескін-

ченності дорівнює одиниці, тт. F (-¥) = lim F (x) = 0 ,	F (+¥) = lim F (x) = 1 .
x®-¥	x®+¥

4. Ймовірність попадання випадкової величини в інтервал [x1 , x2 ) дорівнює прирощенню її функції розподілу на цьому інтервалі, тт.

P (x1 £ X < x2 ) = F (x2 ) - F (x1 )		(1.30)
Приклад 1.22. Випадкова величина Х задана функцією розподілу ймовірностей
ì0,	якщо x £ 2
F (x )= íï x(- 2)2 , якщо 2 < x £ 3
ï	якщо x > 3
î1,
Знайти ймовірність попадання випадкової величини в інтервал (2,5; 3,5).
Розв’язання. Ймовірність попадання випадкової величини X		в заданий інтер-
вал обчислюємо за формулою (1.30)
P (2,5 < X < 3,3) = F (3,5) - F (2,5) = 1- 0, 25 = 0, 75 .

Щільністю ймовірності (щільністю розподілу або просто щільністю) f (x)

неперервної випадкової величини X називається похідна її функції розподілу

f (x) = F ¢(x)

(1.31)

Щільність імовірності іноді називають диференціальною функцією або дифе-

ренціальним законом розподілу.

Графік щільності ймовірності називають кривою розподілу. Приклад 1.23. Випадкова величина X задана функцією розподілу

ì0,		якщо x £ 0
ï	1
F (x )= íï		(1 - cos x), якщо 0 < x £ p .

ï2		якщо x > p
ï1,
î

Знайти диференціальну функцію.

Розв’язання. Використавши формулу (1.32), отримаємо

ì0,			якщо x £ 0
ï	1
f (x )= íï		sin x,	якщо 0 < x £ p .

ï2			якщо x > p
ï0,
î

Властивості щільності ймовірностей

1. Щільність ймовірності невід’ємна функція, тт.

f(x) > 0

2.Ймовірність попадання неперервної випадкової величини в інтервал[ a, b ]

дорівнює визначеному інтегралу від її щільності ймовірності в межах від a до b , тт.

b
P (a £ X £ b) = ò f (x )dx	(1.32)

3. Функція розподілу неперервної випадкової величини може бути записана через щільність за формулою

x
F (x )= ò f (x )dx	(1.33)

-¥

4. Невласний інтеграл в нескінченних межах від щільності ймовірності неперервної випадкової величини дорівнює одиниці:

+¥

ò f (x )= 1.

-¥

Приклад 1.24. Щільність ймовірності неперервної випадкової величини X

ì0,		якщо x £1
ï	1
f (x )= íïx -	1	, якщо 1 < x £ 2 .
f (x )= íïx -	2	, якщо 1 < x £ 2 .
ï	2	якщо x > 2
ï0,		якщо x > 2
î

																																23
Знайти функцію розподілу F (x)			і побудувати графіки										f (x)				і F (x) .
Розв’язання. Використовуючи формулу(1.33) для кожного з інтервалів знай-
демо F (x) .
1). Якщо x £1 , то		f (x) = 0 , отже
						x
			F (x )= ò f (x )dx = 0 .
						-¥
2). Якщо 1 < x £ 2,		f (x )= x -		1	, отже
2). Якщо 1 < x £ 2,		f (x )= x -			, отже
			2													x
1	x	1		x		æ		1	ö	æ x2				x ö				x2		x		1				1					x2	- x
1	x	1		x		æ		1	ö	æ x2				x ö				x2		x		1				1					x2	- x
F (x )= ò f (x )dx + ò f (x )dx = ò 0dx + ò						ç x	-		÷dx = ç			-			÷		=		-		-			+				=					.
F (x )= ò f (x )dx + ò f (x )dx = ò 0dx + ò						ç x	-	2	÷dx = ç			-			÷		=		-		-			+				=				2	.
-¥	1	-¥	1			è		2	ø	è 2 2					ø	1		2 2 2 2														2
-¥	1	-¥	1							è 2 2					ø	1
3). Якщо x > 2, f (x) = 0 , отже
1	2	x				1			2	æ	1 ö						x			æ x2					x ö				2
1	2	x				1			2	æ	1 ö						x			æ x2					x ö				2
F (x )= ò f (x )dx + ò f (x )dx + ò f (x )dx = ò 0dx + òç x -													÷dx + ò0dx =							ç			-				÷			=
													÷dx + ò0dx =							ç			-				÷			=
-¥	1	2				-¥			1	è	2 ø						2			è	2 2 ø								1
-¥	1	2				-¥			1								2			è	2 2 ø								1

= 2 -1 - 1 + 1 = 1. 2 2

Таким чином функція розподілу має вигляд:

ì0,		якщо x £ 1
ï
ï x2 - x
F (x )= í		, якщо 1 < x	£ 2 .
F (x )= í	2	, якщо 1 < x	£ 2 .
ï	2	якщо x > 2
ï1,		якщо x > 2
î
Будуємо графіки функцій f (x)	і F (x) (рис. 6 і рис. 7).
f (x)
f (x)	1

2	2

1	1

0	1	2	х	0	1	2	х
	Рис. 6					Рис. 7

Математичним сподіванням неперервної випадкової величини Х, можливі значення якої належать відрізку [a, b] , називають визначений інтеграл

		b
M (X )= òx × f (x )dx						(1.34)
		a
Якщо можливі значення належать до усієї осі Ox , то
		+¥
M ( X )= ò x × f (x )dx						(1.34')
		-¥
Дисперсією неперервної випадкової величини називають математичне споді-
вання квадрата її відхилення.
Якщо можливі значення X належать відрізку [a; b] , то
D ( X )=	b	éx - M (X	)ù2 × f (x )dx ,
D ( X )=	ò	éx - M (X	)ù2 × f (x )dx ,			(1.35)
	ò	ë	û
	a
якщо можливі значення належать до усієї осі Ox , то
D ( X )=	+¥
D ( X )=		éx - M (X )ù2 × f (x )dx .				(1.35')
	ò ë		û
	-¥
Зауваження. Для обчислення дисперсії неперервної випадкової величини мож-
на використовувати більш зручні формули
D ( X )=	b	x2 × f (x )dx - éM (X			)ù2
D ( X )=	ò	x2 × f (x )dx - éM (X			)ù2	(1.36)
	ò		ë		û
або	a
або
D ( X )=	+¥				)ù2 .
D ( X )=	ò	x2 × f (x )dx - éM (X			)ù2 .	(1.36')
	ò		ë		û
	-¥
Середнє квадратичне відхилення неперервної випадкової величини визна-
чається як і для величини дискретної рівністю
		s ( X )=		)
		s ( X )=	D ( X	)		(1.37)

Приклад 1.25. Дана інтегральна функція:

ì0, якщо x £ 0

F (x )= ïíx2 , якщо 0 < x £ 1

ïî1, якщо x > 1

Знайти: математичне сподівання, дисперсію, середнє квадратичне відхилення. Розв’язання. Знайдемо спочатку диференціальну функцію:

ì0,	якщо x £ 0
f (x )= íï2x,	якщо 0 < x £ 1 .
ï	якщо x > 1
î0,	якщо x > 1

Обчислимо математичне сподівання за формулою (1.34)

дисперсію за формулою (1.36):

або

æ 2 ö

dx -

= 2 ×

x4 1

dx = x

3 b

= b

D (X )= ò x

2xdx - ç

= 2ò x

f (x )dx = ò 0dx + ò3x

= 2

3 ø

4 0

9 2 9 18

-¥

середнє квадратичне відхилення за формулою (1.37):

звідки b = Me (X )=

» 0, 79

s ( X )=

1 » 0, 23 .

3 2

Математичне сподівання обчислюємо за формулою (1.34')

+¥

Модою M o (X )

випадкової величини X називається її найбільш вірогідне

M (X

x × f

(x )dx =

0 ×dx +

x ×

(

3x2

dx +

0 ×dx = 3 × x4

= 0, 75

значення (при якому ймовірність

або щільність ймовірності

f (x)

досягає макси-

)

-¥

Взаємне

розташування точок M (X ),

Me (X ) і

Mo ( X ) в

порядку

зростання

муму).

абсцис вказано на рис.8.

Медіаною Me (X )

неперервної випадкової величини X називається таке її

значення, для якого

1.6. Основні закони розподілу

P (X < Me ( X ) = P (X > Me(X ) =

(1.38)

Основні закони розподілу для дискретних і неперервних величин разом з їх чи-

словими характеристиками наведемо в таблицях 1.1 і 1.2.

Приклад 1.26. Знайти моду, медіану і математичне сподівання випадкової ве-

а) Дискретна випадкова величина

Таблиця 1.1

личини Х, яка задана щільністю ймовірності

№

Закони

Обчислення ймовірності

Числові характеристики

ì0,

якщо

x £ 0

якщо

0 < x £ 1.

n/n

розподілу

Pn (m)

M (x)

D (x)

f (x )= í3x

ï0,

якщо

x > 1

Біномний

Cnm pm qn-m ,

npq

де 0 < p < 1 ,

q =1 - p

Розв’язання. Крива розподілу представлена на рис. 8

Пуассона

lm × e-l

f (x)

де l = np

Геометри-

p ×qm-1

чний

×C n-m

M ö

n ×

N -M ,

ç1

C n

N -1

N ø

де

де N – сукупність

Гіпергео-

m = 0,1,...min (n; m) ;

об’єктів;

×ç1

0,5

метричний

M – кількість

m £ N , n £ N ;

об’єктів, які мають

M (X )

Me ( X ) M o ( X )

n, M , N – натуральні чи-

Рис. 8

такі ж властивості

сла

Очевидно, що щільність ймовірності f (x)

максимальна

при x = M o (X ) =1 .

Медіану Me (X ) = b знайдемо з умови

f (x )dx = 1

-¥

б) Неперервна випадкова величина

Таблиця 1.2

№

Закони

Функція розподілу

Щільність ймовірності

Числові характе-

n/n

розподілу

F (x)

f (x)

ристики

M (x)

D (x)

Рівно-

ì0

при x £ a

ì0

при x < a

мірний

- a

ï x

при a < x £ b ,

при a < x £ b

(b - a)2

- a

a + b

ïb

при x > b

ïb

при x > b

ï1

ï0

де a і b – кінці від-

різка (a < b)

Показ-

ì0

при x < 0

ì0

при x < 0

никовий

í1- e-lx при x ³ 0

(експо-

île-lx

при x ³ 0

ненціа-

де l – параметр екс-

льний)

поненти

Нор-

æ x - a ö

маль-

Ф ç

÷ ,

ний

де

Ф (x )=

òe-

dt ,

-(x -a)2

× e

2s 2

s 2

x - a

де t =

; a – ма-

тематичне сподівання;

s – середнє квадра-

тичне відхилення

Лога-

ln x

(t -ln a)2

рифмі-

ò e

2s 2

dt ,

чно-

s ×

-¥

(ln x -ln a)2

норма-

де t

x - a

;

a – ма-

× e

2s 2

s 2

×e

(es 2 -1)

льний

s ×

2p × x

a ×e

тематичне сподівання;

s – середнє квадрати-

чне відхилення

Розділ 2. МАТЕМАТИЧНА СТАТИСТИКА

2.1. Основні поняття математичної статистики Генеральна сукупність – уся група об’єктів, що підлягають вивченню.

Вибірка – частина об’єктів генеральної сукупності, що потрапили на перевірку або дослідження.

Обсяг генеральної сукупності (вибірки) – число елементів генеральної сукупності (вибірки): N, (n).

Варіант – кожне окреме значення ознаки (x1 , x2 ,..., xi ) .

Частота – число, що показує скільки разів зустрічається той або інший варіант

(n1 , n2 ,..., ni ) .

Статистичний ряд розподілу – упорядкована статистична сукупність. Ранжирований ряд – ряд чисел ознаки, яка варіює, що знаходяться в порядку

зростання або спадання.

Варіаційний ряд – ранжирований у порядку зростання або спадання ряд варіантів з відповідними їм частотами.

Дискретний ряд – ряд, у якому окремі значення ознаки (варіанти) відрізняються друг від друга на деяку скінчену величину.

Неперервний ряд (інтервальний) – ряд, у якому значення ознаки відрізняються одне від одного на як завгодно малу величину.

Статистичним інтервальним розподілом – називається відповідність між ін-

тервалами вибірки, частотами і відносними частотами.

Відносною частотою p* (частістю)				–	називають відношення частоти n , що
i							i
відповідає значенню xi до суми всіх частот (обсягу вибірки).
p* =	ni	=	ni	,	i =		,
						1, k
	åni		n
i

де k – кількість інтервалів

При переході від інтервального ряду розподілу до дискретного припускають, що частоти згруповані в центрах інтервалів:

xi* = xi +1 + xi

Атрибутивний ряд – ряд, у якому значення ознаки не має кількісного вираження.

Гістограма відносних частот – ступінчаста фігура, що складається з прямокутників, основами яких служать інтервали [xi ; xi +1 ], а висоти рівні pi* .

Полігон відносних частот – ломана, з’єднуюча точки (xi* , pi* ).

Діаграма – значення ознаки, виражене в процентному відношенні. Емпіричною функцією розподілу випадкової величини Х називається функція

F x (x) = nx , n

де nx – число спостережень вибірки, менших за х.

Властивості емпіричної функції розподілу:

1.Значення F* (x) Î[0;1] .

2.F * (x) – не спадна функція.

3.F* (x0 ) = 0, F * (xk ) = 1 , де xk – найбільше значення.

2.2.Числові характеристики варіаційного ряду

Види характеристик

згруповані

не згруповані

Вибіркова середня

å xi × ni

å xi

x =

i =1

x =

i =1

å(xi

- x)

å(xi - x)

i =1

або

D =

i =1

Дисперсія

або

åx2 × ni

i =1

åx

× ni

D =

- x

i =1

Виправлена дисперсія

и =

n -1

Середнє квадратичне

s =

відхилення

×100%

Коефіцієнт варіації

– слабка;

6-10%

– помірне;

16-20%

– значне;

21-50%

– велике;

>50

– дуже велике

(для малих вибірок < 33%)

– варіант, що має максимальну частоту, для інтерва-

льного ряду: M o

= xMomin + h

nMo - nMo-1

2nMo - nMo+1 - nMo-1

Мода

nMo – частота модального інтервалу,

nMo-1

– частота інтервалу, що передує модальному,

nMo+1

– частота наступного інтервалу за модальним,

xMomin

– нижня границя модального інтервалу.

– середина ранжированого ряду для інтервального

Медіана

ряду: M e =

M0 +

2.3.Вибірковий метод

В практиці статистичних спостережень розрізняють два види спостережень: суцільне, коли вивчаються усі об’єкти в сукупності, і несу цільне, вибіркове, коли вивчається частина об’єктів.

Сутність вибіркового метода складається в тім, що по деякій частині генеральної сукупності (вибірці) виносять рішення про її властивості в цілому.

Переваги вибіркового метода спостережень в порівнянні з суцільним:

–дозволяє суттєво економити матеріальні, трудові, часові затрати;

–є єдино можливим у випадку нескінченної генеральної сукупності;

–дає можливість поглибленого дослідження за рахунок програми дослідження;

–дозволяє знизити помилки реєстрації, тт. Розходження між дійсними і зареєстрованими значеннями ознаки.

Основний недолік виборчого метода

–помилки дослідження, які називаються помилками репрезентативності (представництва).

Вибірка називається репрезентативною (представницькою), якщо вона достатньо добре відтворює генеральну сукупність.

Розрізняють слідуючи види вибірок:

–власно-випадкова;

–механічна;

–типова (стратифікована);

–серійна (гніздова).

Використовують два способи утворення вибірки:

oповторний відбір (по схемі поверненої кулі), коли кожний елемент, випадково відібраний і обстежений повертається в загальну сукупність і може бути повторно відібраний;

oбез повторний відбір(по схемі неповернутої кулі), коли відібраний елемент не повертається в загальну сукупність.

Задачею виборчого методу є оцінкапараметрів (характеристик) генеральної сукупності по даним вибірки.

Теоретичну основу застосування виборчого методу складаєзакон великих чисел, згідно з яким при необмеженім збільшенні об’єму вибірки практично достовірно, що випадкові виборчі характеристики як завгодно близько наближаються(збігаються по ймовірності) до визначених параметрів генеральної сукупності.

Алгоритм вибіркового методу

1.Визначити розмах вибірки: D = xmax - xmin ;

2.Побудувати ранжирований ряд;

3.Визначити кількість інтервалів за формулою Стерджесса

			(де n – обсяг вибірки);
k =1 + 3, 21×lg n або k = n ,

4. Обчислить довжину інтервалу: h = D , k

де xmin £ a , xmax ³ b ;

5)Побудувати інтервальний ряд розподілу, гістограму;

6)Побудувати дискретний ряд розподілу, полігон;

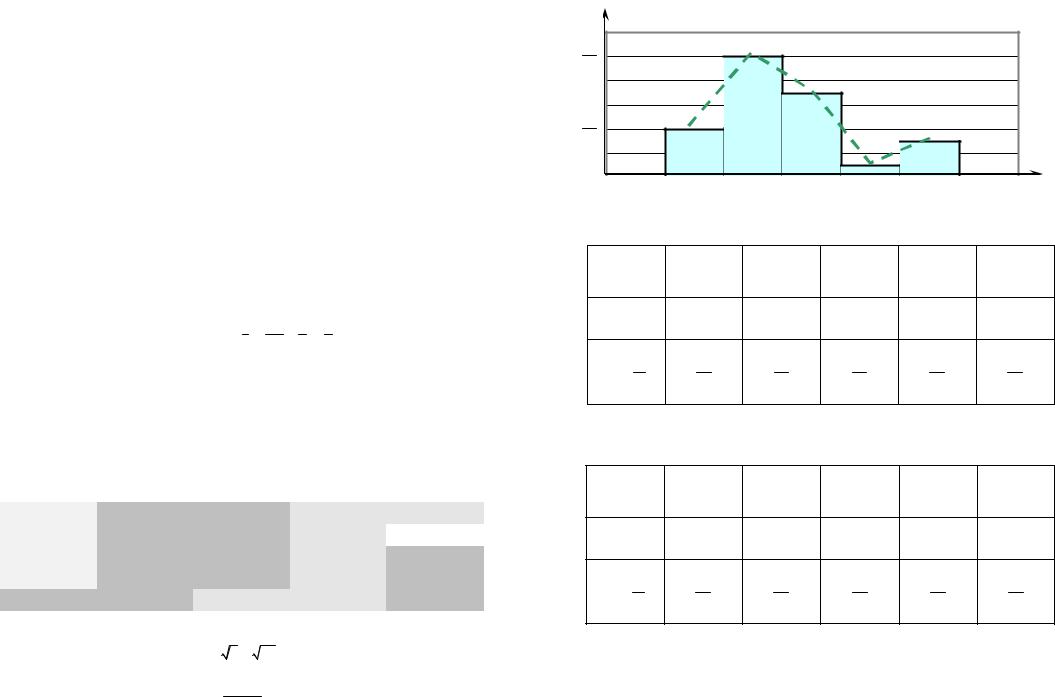
							31	32
7) Обчислити числові характеристики: середнє значення,					дисперсію, середнє			pi*
квадратичне відхилення, моду, медіану, коефіцієнт варіації; зробити висновок.
Приклад 2.1. Отримані вибіркові дані про врожайність зернових культур(ц/га)								10
								25
по господарствам Запорізької області за 2002 рік:								25
13,4	13,6	17,8		15,4			24,5	4
17,6	18,2	16,8		19,3			19,4	4
17,6	18,2	16,8		19,3			19,4	25
								25
16,1	16,1	17,2		19,8			26,7
15,9	26,1	21,7		19,9			19,4				13		15,8		18,6	21,4	24,2		27	xi
											13			,8	,6	,4		,2		7
17,2	16,1	15,7		20,3			20,5				13		15		Рис. 9	21		24	2
17,2	16,1	15,7		20,3			20,5						15		18	21		24
Використовуючи вибірковий метод:								Складемо інтервальний ряд розподілу:
Використовуючи вибірковий метод:
1) визначити розмах вибірки;										xi		13 – 15,8			15,8 – 18,6	18,6 – 21,4		21,4 – 24,2		24,2 - 27
	побудувати:									xi		13 – 15,8			15,8 – 18,6	18,6 – 21,4		21,4 – 24,2		24,2 - 27
	побудувати:
2) ранжирований ряд;
3) інтервальний ряд, гістограму;										ni			4		10	7		1		3
4) дискретний ряд, полігон;										ni			4		10	7		1		3
5) обчислити числові характеристики: x,			Dи ,	s , V , M 0 ,	M e ,	As ,	E		p* = ni
6) зробити висновок на підставі отриманих числових характеристик.									p* = ni				4		10	7		1		3
Розв’язання. Обсяг вибірки (кількість елементів): n = 25									i	n			25		25	25		25		25
1. Визначимо максимальний і мінімальний варіант вибірки:										n			25		25	25		25		25
1. Визначимо максимальний і мінімальний варіант вибірки:
	xmin =13, 4		xmax	= 26, 7 .				Для отриманого ряду розподілу побудуємо гістограму відносних частот (рис. 9)
Розмах вибірки обчислимо по формулі:
	R = xmax - xmin	= 26, 7 -13, 4 = 13, 3						4. Для переходу до дискретного ряду розподілу, припускаємо, що частоти згрупова-
2. Побудуємо ранжирований ряд, розташувавши значення вибірки в зростаючому по-								ні в центрах інтервалів

рядку:										xi*			14,4		17,2	20		22,8		25,6
										xi*			14,4		17,2	20		22,8		25,6
13,4	16,1	17,2		19,4			20,5
13,6	16,1	17,6		19,4			21,7			ni			4		10	7		1		3
15,4	16,1	17,8		19,8			24,5
15,7	16,8	18,2		19,9			26,1		p* = ni				4		10	7		1		3
15,9	17,2	19,3		20,3			26,7		i	n			25		25	25		25		25
15,9	17,2	19,3		20,3			26,7			n			25		25	25		25		25
3. Для побудови інтервального ряду розподілу, визначимо кількість інтервалів роз-
бивки за формулою:								Побудуємо полігон відносних частот (зобразимо на гістограмі).
	k =	n =	25 = 5
	k =	n =	25 = 5					1.	Обчислимо числові характеристики вибірки даних:
Крок інтервалу визначаємо за формулою:								1.	Обчислимо числові характеристики вибірки даних:
Крок інтервалу визначаємо за формулою:								– середнє значення:
	h = 27 -13 = 2,8							– середнє значення:
	h = 27 -13 = 2,8

x = 14, 4 ×4 +17, 2 ×10 + 20 ×7 + 22,8 ×1+ 25, 6 ×3 = 18, 77 25

– дисперсію:

D = 14, 42 ×4 +17, 22 ×10 + 202 ×7 + 22,82 ×1+ 25, 62 ×3 -18, 772 = 10, 64 25

– виправлену дисперсію:

×10, 64 =11, 08

n -1

– середнє квадратическое відхилення:

s =

» 3, 26

11, 08

– коефіцієнт варіації:

×100% =

3, 26

×100% = 17, 37%

18, 77

– моду:

10 - 4

M 0

=15,8 + 2,8 ×

» 17, 67

2 ×10 - 4 - 7

– медіану:

M e

17, 67 +

×18, 77 =18, 4

Висновок: У цілому по господарствам Запорізької області середня врожайність зер-

нових культур складає 15,51 – 22,3 (ц/га), (x ±s ) . Причому в більшій частині госпо-

дарств отриманий урожай 17,67(ц/га), (M 0 ) . У цілому по області розсіювання за ре-

зультатами врожайності значне (V =17,37%)

2.3 Кореляційний аналіз Функціональним називають зв’язок між ознаками, при якому кожному зна-

ченню однієї змінної відповідає чітко окреслене значення іншої змінної. Кореляційним (статистичним) зв’язком називається такий зв’язок, при якому

чисельному значенню однієї змінної відповідає кілька значень іншої.

Кореляційною залежністю y від x називається така залежність при якій зміни випадкової величини x спричиняють зміни середнього значення змінноїy ( yx ), тобто

yx = f (x) .

Вибірковим коефіцієнтом кореляції називається число:

	n
r =	åxi yi	- n	x	y	,
	i =1

ns x s y

åxi

å yi

де

x, y – вибіркові середні для x і y , тобто x =

y =

s x , s y – вибіркові середньоквадратичні відхилення для x і

å xi2

å yi2

s x = s

- x

s y = s

y =

- y

Властивості коефіцієнта кореляції:

абсолютна величина коефіцієнта кореляції не перевершує 1

£ 1

якщо r = ±1, то x і y

зв’язані точкою лінійного зв’язку:

y = ax + b ;

якщо r = 0 ,

то між x

y немає лінійного зв’язку,

але криволінійна залежність

можлива;

чим ближче r

до ±1 , тим сильніший лінійний зв’язок між x і

y і, чим ближче r

до 0 , тим він слабкіший;

якщо r > 0 , зв’язок між x і y

зростаючий,

r < 0 , зв’язок – спадний (рис. 10)

спадний

зростаючий

0,5

-1

-0,5

слабкий

сильний

Рис. 10

Рівняння лінійної регресії

y = ax + b .

Параметри лінійної регресії рівні:

a = r

s y

b =

- ax

Перевірка гіпотези про значимість коефіцієнта кореляції.

Гіпотеза Ho – лінійного кореляційного зв’язку немає для даної генеральної сукупнос-

ті.

а) Визначаємо значення критерію, що спостерігається

n - 2 tcп = r 1- r 2 .

б) по таблиці Ст’юдента визначають tкрит = (a, k = n - 2) . в) при tсп ³ tкрит – нульову гіпотезу відкидають,

при tсп < tкрит – Ho приймають.

Приклад 2.2. Знайти коефіцієнт кореляції і рівняння лінійної регресії для зада-

ної залежності врожайності y			(ц/га) від якості ґрунту		x (у балах). Перевірити коефі-
цієнт кореляції на значимість.
	xi	–1		0	1	4
	yi	–1		2	0	2

Розв’язання. Для зручності обчислень складемо розрахункову таблицю:

	x	y	xi yi	x2	y2
	i	i		i	i
	–1	–1	1	1	1
	0	2	0	0	4

	1	0	0	1	0

å	4	2	8	16	4
å	4	3	9	18	9

Обчислимо середні значення для х і у:

x	= åxi =	4	= 1 ;	y	= å yi =	3	;	(n=4)
		4				4
	n				n

Обчислимо середні квадратичні відхилення для х і у:

s x	=	18 - 4 ×12	=1,87 ;	s y	=	9 - 4 ×0, 752	=1, 3 .

	4				4

Обчислюємо коефіцієнт кореляції:

r = 9 - 4 ×1×0, 75 = 0, 62 . 4 ×1,87 ×1,3

На підставі властивостей коефіцієнта кореляції робимо висновок.

Оскільки r = 0,62 > 0 , то між x і y сильний, зростаючий лінійний кореляцій-

ний зв’язок. Обчислюємо коефіцієнти лінійної регресії y = ax + b :

		3				y = 0,43x + 0,32
		3				y = 0,43x + 0,32
		2


		1
		1
		0

-4	-2			0	2		4	6
			-1



		-2
						Рис.11
						Рис.11

36
a =	0, 62 ×1, 3	= 0, 43	;	b = 0, 75 - 0, 43 = 0,32

1, 87
Рівняння лінійної регресії має вигляд: y = 0, 43x + 0,32
Побудуємо на координатній			площині	задані пари точок і отримаємо пряму
(рис. 11).

Перевіримо коефіцієнт кореляції на значимість.

Ho : r = 0 – для даної генеральної сукупності лінійного кореляційного зв’язку немає. а) Обчислюємо значення критерію, що спостерігається

t = 0, 62 ×		4 - 2	» 1,12 .
t = 0, 62 ×	1- 0, 622		» 1,12 .
	1- 0, 622
б) За таблицею Ст’юдента визначаємо
tкрит (a = 0, 05,		k = n - 2 = 4 - 2 = 2) = 4,30 .

в) Оскільки tсп < tкрит (1,12 < 4,30) нульову гіпотезу відкидаємо, тобто коефіцієнт кореляції для всієї генеральної сукупності не дорівнює нулю.

2.4. Однофакторний дисперсійний аналіз

Дисперсійний аналіз – це математико – статистичний метод визначення результатів спостереження, залежних від різноманітних одночасно діючих факторів.

Алгоритм однофакторного дисперсійного аналізу

1. Складають розрахункову таблицю у такому вигляді:

Рівень			Повторності			Середнє	R	R2	P
Рівень							i	i	i
		1	2	...	n
І		x11	x12	...	x1n
ІІ		x21	x22	...	x2n
...		...	...	...	...
m		xm1	xm 2	...	xmn
	n						åRi	åRi2	åPi
	n
де Ri	= åxij – сума значень ознаки на кожнім рівні,

j =1

Pi = åxij2 – сума квадратів значень ознаки на кожнім рівні;

j=1

2.Обчислюють суми (загальну, факторну, залишкову):

Sзаг = åPi -

êé

åRi úù

Sфакт

åRi2 -

êé

åRi úù

, Sзал = Sзаг - Sфакт ;

i =1

mn ë i =1

n i =1

mn ë i =1

3. Обчислюють дисперсії (факторну, залишкову):

	sфакт2 =	Sфакт	,	s зал2 =		S	зал
	sфакт2 =	n -1	,	s зал2 =		n (m -1)
		n -1				n (m -1)
4.	Обчислюють значення функції, що спостерігається.
				s 2
		F =		факт	.
		F =			.
		p		s 2
				зал
5.	На підставі обчислених	степенів вільності( k1 = n -1 k2 = n ×(m -1) ) і рівня

значимості a = 0, 05 , визначають по таблиці F – критерію Фішера-Снедекора критичне значення Fкрит (додаток 5).

Висновок: згідно критерію Фішера, якщо

Fp > Fкрит – розходження групових середніх не значиме, фактор не впливає Fp < Fкрит – фактор впливає.

Приклад 2.3. За результатами дослідів перевірити чи впливає сорт пшениці на зміст білка в зерні.

Розв’язання. Для зручності обчислень складемо розрахункову таблицю:

Рівень		Повторності			Ri	x	= åRi	Pi	R2
(сорт)	1		2	3		i	m		i
(сорт)	1		2	3			m
1	0		1	0	1		1/3	1	1

2	1		1	1	3		1	3	9

3	1		2	0	3		1	5	9
4	1		0	0	1		1/3	1	1

åRi = 8

åPi = 10 åRi2 = 20

За умовою m = 4 ,

n = 3 .

Обчислимо суми:

Sзаг =10 -

= 4, 67, Sфакт =

= 1,34,

Sзал

= 4, 7 -1,34 = 3,33 ,

Обчислимо дисперсії

s зал2 = 3,33 (3×(4 -1)) =0, 37

sфакт2

= 1,34 / (3 -1) = 0, 67 ,

Обчислимо значення, що спостерігаються і критичні значення функції:

F =

sфакт2

0,67

= 1,81,

= 3 -1 = 2,

= 3(4 -1) = 9

sзал2

0,37

Fкрит = 4, 26 ( по значенням k1

і k2

приa = 0, 05 ).

4)Оскільки

Fp < Fкрит – фактор (сорт пшениці) суттєво впливає на кількість білка в зерні.

Розділ 3. ТЕОРЕТИЧНІ ПИТАННЯ ТА ЗАВДАННЯ ДО ТИПОВОГО РОЗРАХУНКУ

ТЕОРЕТИЧНІ ПИТАННЯ

1.Основні поняття теорії ймовірностей.

2.Класичне, статистичне і геометричне означення ймовірностей.

3.Основні поняття комбінаторики.

4.Теорема додавання ймовірностей несумісних подій.

5.Повна група подій. Протилежні події.

6.Добуток подій. Умовна ймовірність. Теорема множення сумісних подій.

7.Незалежні події. Теорема множення незалежних подій. Надійність механізмів, приладів і систем.

8.Імовірність появи хоча б однієї події.

9.Теореми додавання ймовірностей сумісних подій.

10.Формула повної ймовірності.

11.Формули Бейеса.

12.Види випадкових величин. Дискретні випадкові величини і їх закони розподілу ймовірностей. Многокутник розподілу.

13.Повторення дослідів. Біноміальний (біномний) закон розподілу. Формула Я. Бернуллі.

14.Найімовірніше число появи подій.

15.Локальна теорема Муавра-Лапласа.

16.Інтегральна теорема Муавра-Лапласа.

17.Асимптотична формула Пуассона. Закон Пуассона розподілу ймовірностей рідкісних подій.

18.Математичне сподівання дискретної випадкової величини і його властивості.

19.Дисперсія дискретної випадкової величини, її властивості. Середнє квадратичне відхилення.

20.Інтегральна функція розподілу ймовірностей випадкової величини, її властивості, графік.

21.Диференціальна функція розподілу ймовірностей неперервної випадкової величини, її властивості, графік. Імовірнісний зміст диференціальної функції.

22.Математичне сподівання, дисперсія, середнє квадратичне відхилення неперервних випадкових величин.

23.Нормальний закон розподілу ймовірностей.

24.Імовірність попадання нормально розподіленої випадкової величини в заданий інтервал.

25.Імовірність заданого відхилення нормально розподіленої випадкової величини від її математичного сподівання. Правило трьох сигм.

26.Оцінки відхилення теоретичного розподілу від нормального. Асиметрія і ексцес.

27.Розподіл c2 .

28.Розподіл Ст’юдента.

29.Розподіл F Фішера-Снедокера.

30.Означення показникового розподілу. Імовірність попадання в заданий інтервал показниково розподіленої величини.

31.Числові характеристики показникового розподілу.

32.Функція надійності. Показниковий закон надійності.

33.Елементи математичної статистики. Вибірковий метод. Повторна і без повторна вибірки.

34.Емпірична функція розподілу.

35.Полігон і гістограма статистичних розподілів.

36.Числові характеристики: генеральна середня і вибіркова середня.

37.Числові характеристики: генеральна дисперсія і вибіркова дисперсія.

38.Оцінка генеральної дисперсії по полагодженій вибірковій.

39.Мода і медіана для дискретних статистичних розподілів вибірки.

40.Мода і медіана для інтервальних статистичних розподілів вибірки.

41.Функціональна, статистична і кореляційна залежності.

42.Виборчі рівняння регресії.

43.Відшукання параметрів виборчого рівняння прямої лінії середньоквадратичної регресії по не згрупованим даним.

44.Кореляційна таблиця.

45.Відшукання параметрів виборчого рівняння прямої лінії регресії по згрупованим даним.

46.Виборчий коефіцієнт кореляції і методика його обчислення.

РОЗРАХУНКОВІ ЗАВДАННЯ

1.Задачі на класичну, статистичну і геометричну ймовірності

1.1.В урні є 10 куль: 3 білих і 7 чорних. З урни навмання виймається одна куля. Яка ймовірність того, що ця куля: а) біла; б) чорна?

1.2.Зі слова «НАВМАННЯ» вибирається навмання одна буква. Яка ймовірність того, що це буква «Я»? Яка ймовірність того, що це гласна?

1.3.Кидають дві гральні кістки. Яка ймовірність випадіння на двох кістках у сумі не менше 9 очок? Яка ймовірність випадіння одиниці, принаймні, на одній кістці?

1.4.Дитина грає з чотирма буквами розрізної абетки А, А, М, М. Яка ймовірність того, що при випадковому розташуванні букв у ряд вона одержить слово «МАМА»?

1.5.При наборі телефонного номера абонент забув дві останні цифри і набрав їх навмання, пам’ятаючи тільки що ці цифри непарні і різні. Знайти ймовірність того, що номер набраний правильно.

1.6.Серед 25 екзаменаційних білетів 5 «гарних». Два студенти по черзі беруть по одному білету. Знайти ймовірності наступних подій: А = {перший студент узяв гарний білет}; В = {другий студент узяв гарний білет}; С = {обидва студенти взяли гарні білети}.

1.7.У партії з 50 виробів 5 бракованих. Навмання вибирається 6 виробів. Визначити ймовірність того, що серед цих 6 виробів 2 бракованих.

1.8.Знайти ймовірність того, що дні народження 12 чоловік прийдуться на різні місяці року.

1.9.У ліфт семиповерхового будинку на першому поверсі ввійшли3 чоловіки. Кожний з них з однаковою ймовірністю виходить на будь-якому поверху, починаючи

здругого. Знайти ймовірності наступних подій: A = {усі пасажири вийдуть на четвертому поверсі}; B = {усі пасажири вийдуть одночасно (на одному поверсі)}; C = {усі пасажири вийдуть на різних поверхах).

1.10.У шафі знаходяться 10 пар черевиків різних ґатунків. Випадково вибирають 4 черевики. Знайти ймовірність того, що серед вибраних черевиків відсутні парні.

1.11.У магазин надійшло 30 холодильників, п’ять з них мають заводський дефект. Випадково вибирається один холодильник. Яка ймовірність того, що він не має дефекту?

1.12.В коробці знаходиться шість однакових по формі і близьких по діаметру свердлів. Випадково свердла виймаються з коробки. Яка ймовірність того, що свердла витягнуться в порядку зростання їх діаметра?

1.13.Комісія з якості раз на місяць перевіряє якість продуктів у двох з 30 магазинів, серед яких знаходиться і два відомих вам магазина. Яка ймовірність того, що на протязі місяця вони обидва будуть перевірені?

1.14. На станцію прибули 10 вагонів різної продукції. Вагони позначені номерами від одного до десяти. Знайти ймовірність того, що серед п’яти відібраних для контролю вагонів будуть вагони з номерами 2 і 5?

1.15.З 20 акціонерних товариств (АТ) чотири є банкрутами. Громадянин придбав по одній акції шести АТ. Яка ймовірність того, що серед куплених акцій дві виявляться акціями банкрутів?

1.16.На склад привезли 50 ящиків комплектуючих виробів для одного з видів ЕОМ, але серед них виявилось чотири ящики комплектуючих для іншого виду ЕОМ.

<<< < Предыдущая 12 / 42 3 4 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
25.08.20191.53 Mб3Metodichka_po_praktitsi-20010-OiA.doc
#
25.08.20193.16 Mб8Metodichka_po_SRS-OA.doc
#
12.11.2019564.22 Кб5Metod_FIN_RIN.doc
#
10.09.2019446.46 Кб2Metod_sam_robota_ekologi.doc
#
24.04.20194.08 Mб14met_ teor_wer_i_mat_st.doc
#
02.03.2016618.53 Кб45met_ teor_wer_i_mat_st.pdf
#
31.08.20193.29 Mб2met_diff_rivn.doc
#
07.12.201883.9 Кб15Microsoft Word.docx
#
02.03.2016882.48 Кб11Microsoft_Word__lektsiya_3_chastina1.pdf
#
02.03.20161.18 Mб25Microsoft_Word__lektsiya_3_chastina2.pdf
#
02.09.201958.28 Кб0mot_rgr.docx