
met_ teor_wer_i_mat_st
.pdf
МІНІСТЕРСТВО АГРАРНОЇ ПОЛІТИКИ УКРАЇНИ МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ ТАВРІЙСЬКИЙ ДЕРЖАВНИЙ АГРОТЕХНОЛОГІЧНИЙ УНІВЕРСИТЕТ
ВИЩА МАТЕМАТИКА * ТАВРІЙСЬКИЙ УНІВЕРСИТЕТ
МЕТОДИЧНІ РЕКОМЕНДАЦІЇ ТА ЗАВДАННЯ ДЛЯ ІНДИВІДУАЛЬНОЇ РОБОТИ СТУДЕНТІВ ДО ТИПОВОГО РОЗРАХУНКУ ЗА ТЕМОЮ:
“ТЕОРІЯ ЙМОВІРНОСТЕЙ ТА МАТЕМАТИЧНА СТАТИСТИКА”
Для підготовки бакалаврів за напрямом 6.080400 “Комп’ютерні науки” і за напрямом 6.100102
“Процеси, машини та обладнання агропромислового виробництва”
2
Методичні рекомендації та завдання для індивідуальної роботи студентів до ти-
пового розрахунку за темою: “Теорія ймовірностей та математична статистика”
/Уклад.: М.О. Рубцов, – Мелітополь, ТДАТУ, 2008. – 74 с.: іл.
Методичні рекомендації та завдання для індивідуальної роботи студентів до ти-
пового розрахунку за темою: “Теорія ймовірностей та математична статис-
тика” містять три розділи: теорія ймовірностей, математична статистика, теоретичні питання та завдання до виконання типового розрахунку. Для бакалаврів за напрямом 6.050101 “Комп’ютерні науки”.
Р е ц е н з е н т и: д.т.н., проф., зав. кафедри інформатики і кібернетики Мелітопольського Державного Педагогічного Університет В.С. Єремєєв; к.т.н., доцент кафедри фізики, теоретичної механіки та ТММ ТДАТУ М.М. Данченко
Розглянуто і затверджено на засіданнях методичних комісій факультету МТ протокол № 4 від 29.95.08 і факультету ІКТ протокол № 9 від 24.06.08.
МЕЛІТОПОЛЬ
2008
3
Зміст |
|
Вступ |
4 |
1. Розділ 1. Теорія ймовірностей |
5 |
1.1. Основні поняття теорії ймовірностей |
5 |
1.2. Теореми додавання і множення |
8 |
1.3. Формула повної ймовірності. Формули Бейеса |
12 |
1.4. Повторення випробувань |
13 |
1.5. Випадкові величини |
16 |
1.5.1. Дискретні випадкові величини і їх числові характеристики |
16 |
1.5.2. Неперервні випадкові величини і їх числові характеристик |
20 |
1.6. Основні закони розподілу |
26 |
2. Розділ 2. Математична статистика |
28 |
2.1. Основні поняття математичної статистики |
28 |
2.2. Числові характеристики варіаційного ряду |
29 |
2.3. Вибірковий метод |
30 |
2.4. Кореляційний аналіз |
33 |
2.5. Однофакторний дисперсійний аналіз |
36 |
3. Розділ 3. Теоретичні питання та завдання до виконання типового |
|
розрахунку |
38 |
Теоретичні питання |
38 |
Розрахункові завдання |
40 |
4. Література |
66 |
Додатки |
67 |
4
ВСТУП
Узв’язку з тим, що в останні часи відбуваються значні зміни в переплануванні багатьох курсів фундаментальних дисциплін, (в тому числі і в курсі з вищої математики) пов’язані з ринковими відносинами і появою інших спеціальностей, тому багато вивчає мого матеріалу виноситься на самостійну роботу. В цілях надання допомоги студентам й інтенсифікації самостійної роботи програмою з курсу вищої математики передбачено виконання типового розрахунку(ТР) по темі: “Теорія ймовірностей та математична статистика”.
Мета методичних рекомендацій– засвоєння теоретичного матеріалу, набуття практичних навичок при розв’язанні задач за вказаною тематикою. В цілому це дає змогу краще підготуватися до семестрового іспиту. Поняття, які містить типовий розрахунок “Теорія ймовірностей та математична статистика” є базовими і на їх основі та аналізі вивчатимуться інші дисципліни, будуть виконуватися курсові і дипломні роботи.
Типовий розрахунок має системний виклад основ теорії ймовірностей та математичної статистики. Він складається з двох частин: теоретичної з розв’язанням типових прикладів та розрахункових завдань, які є індивідуальними для кожного студента.
Урезультаті вивчення студент повинен засвоїти:
–обчислення ймовірностей простих і складних подій;
–основні теореми складання і множення подій;
–формулу повної ймовірності. Формули Бейеса;
–методику обчислення повторних випробувань;
–числові характеристики випадкових величин (дискретних і неперервних);
–обчислення функції розподілу випадкової величини.
Знати алгоритми статистичних методів:
–вибіркового методу;
–кореляційного аналізу, МНК;
–дисперсійного аналізу.
Вміти застосовувати на практиці вивчені методи та алгоритми розрахунків за даними темами, робити висновки за отриманими результатами.
ТР виконується на листах паперу формату А4. Зразок титульного листа наведено у додатку 6.
|
|
|
|
|
|
|
|
5 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Розділ 1. ТЕОРІЯ ЙМОВІРНОСТЕЙ |
|
|
|
|
Властивості ймовірностей подій |
0 £ p( A) £ 1 |
|
||||||||||||||
1.1. Основні поняття теорії ймовірностей |
|
|
|
1. Ймовірність любої події заключна між нулем і одиницею, тт. |
|
|||||||||||||||||
|
|
|
2. Ймовірність вірогідної події дорівнює одиниці. |
|
|
|
|
|||||||||||||||
Подія ( позначається прописними буквами латинського алфавіту: А, В, С) – це |
|
|
|
|
|
|||||||||||||||||
|
3. Ймовірність неможливої події дорівнює нулю. |
|
|
|
|
|||||||||||||||||
будь - який факт, що може відбутися або не відбутися в результаті випробування. |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Під випробуванням (іспитом) розуміється виконання певного комплексу умов, |
|
Статистичною ймовірністю події А називається відносна частота появи цієї по- |
||||||||||||||||||||
в яких спостерігається те чи інше явище і фіксується той чи інший результат. |
дії в n проведених випробуваннях, тт. |
|
|
|
|
|
|
|||||||||||||||
Подія |
називається вірогідною, |
|
якщо |
|
в |
результаті |
випробування |
вона |
|
|
|
|
p%( A) = W ( A) = m , |
|
|
|
|
|
||||
обов’язково відбудеться. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1.2) |
||||||
Подія називається неможливою, |
якщо в результаті випробування вона ніколи |
|
|
|
|
|
|
|
n |
|
|
|
|
|
||||||||
не відбудеться. |
|
|
|
|
|
|
|
де p%( A) |
– статистична ймовірність події A ; W ( A) – відносна частота події A ; |
m – |
||||||||||||
Подія називається випадковою, якщо в результаті випробування вона або від- |
число іспитів, в яких з’явилась подія A ; n – загальне число іспитів. |
|
|
|
||||||||||||||||||
будеться або ні. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Події |
називаються несумісними, якщо поява однієї з них виключає появу ін- |
|
Приклад 1.2. По цілі |
|
зроблено 20 пострілів, причому зафіксовано 18 влучень. |
|||||||||||||||||
шої. В протилежному випадку події називаються сумісними. |
|
Знайти відносну частоту влучень в ціль. |
|
|
|
|
|
|
||||||||||||||
Події називаються рівно можливими, якщо в результаті випробування за умо- |
|
Розв’язання. Нехай подія A – влучення в ціль. Всього було зроблено n = 20 по- |
||||||||||||||||||||
вою симетрії ні одна з цих подій не є об’єктивно більш можливою. |
|
стрілів, з них m =18 влучень. Тоді відносна частота влучень в ціль за формулою (1.2) |
||||||||||||||||||||
Декілька подій називаються єдино можливими, якщо в результаті випробувань |
дорівнює W ( A) = m = 18 = 0, 9 . |
|
|
|
|
|
|
|
||||||||||||||
обов’язково повинна відбутися хоча б одна з них. |
|
|
|
|
|
|
|
|
|
|
||||||||||||
Декілька подій утворюютьповну групу (повну систему), якщо вони є єдино |
|
|
n |
20 |
|
|
|
|
|
|
|
|
|
|||||||||
можливими і несумісними результатами випробувань. Це означає, що в результаті ви- |
|
Одним з недоліків класичного означення ймовірності, обмежуючим його засто- |
||||||||||||||||||||
пробувань обов’язково повинна відбутися одна і тільки одна з цих подій. |
сування, є те, що воно передбачає кінцеве число можливих результатів випробувань. |
|||||||||||||||||||||
Частинним випадком подій, що утворюють повну групу єпротилежні події. |
|
Якщо позначити міру (довжину, площу, об’єм) області через mes, то геометрич- |
||||||||||||||||||||
Дві несумісні події, з яких одна повинна обов’язково відбутися, називаються проти- |
ною |
ймовірністю події A |
|
називається |
відношення |
міри області сприятливої |
появі |
|||||||||||||||
лежними. |
|
|
|
|
|
|
|
|
події |
A до міри усієї області, тт. |
|
mes g |
|
|
|
|
|
|||||
Чисельна міра степені об’єктивної можливості появи події називаєтьсяймовір- |
|
|
|
|
|
p( A) = |
, |
|
|
(1.3) |
||||||||||||
ністю події. |
|
|
|
|
|
|
|
|
|
|
|
|
|
mes G |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Це означення, якісно відтворююче поняття ймовірності події, не є математич- |
де g – фігура, яка сприяє появі події A ; G – фігура, на яку навмання кидається точка. |
|||||||||||||||||||||
ним. Щоб воно таким було, необхідно визначити його кількісно. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Випадок називається сприятливим події А, якщо поява цього випадку веде за |
|
Приклад 1.3. Два лиця A і B |
домовилися зустрітися в визначеному місці, при |
|||||||||||||||||||
собою появу події А. |
|
ймовірності. Згідно класичному означенню |
цьому кожний з’являється туди в любий момент часу між 11 і 12 годинами і дожидає |
|||||||||||||||||||
В дійсності існує три означення |
на протязі 20 хвилин. Якщо партнер до цього часу ще не прийшов або вже покинув до- |
|||||||||||||||||||||
ймовірність події А дорівнює відношенню числа випадків, сприяючих їй до загально- |
||||||||||||||||||||||
мовлене місце, зустріч не відбулася. Знайти ймовірність того, що зустріч відбудеться. |
||||||||||||||||||||||
го числа випадків, тт. |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
Розв’язання. Позначимо моменти приходу в визначене місце лиць A і B через |
||||||||||||||
|
|
m |
|
|
|
|
|
|
|
|||||||||||||
|
p( A) = |
, |
|
|
|
|
(1.1) |
x і y . В прямокутній системі координат xOy візьмемо за початок відліку 11 годин, а |
||||||||||||||
|
n |
|
|
|
|
за одиницю вимірювання –1 год. За умовою 0 £ x £ 1, 0 £ y £1 . Цим нерівностям |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||
де m – число випадків, сприяючих події А; n – загальне число подій. |
|
y |
|
|
задовольняють координати любої точки, |
що належить ква- |
||||||||||||||||
|
|
|
|
|
|
|
|
|
K |
|
||||||||||||
Приклад 1.1. В урні 12 куль: 3 білих, 4 чорних і 5 червоних. Яка ймовірність |
1 |
L |
драту OKLM зі стороною 1 . Нехай подія C – зустріч двох |
|||||||||||||||||||
|
лиць – відбудеться, якщо різниця між x |
і y |
не перевищує |
|||||||||||||||||||
|
|
|||||||||||||||||||||
витягнути з урни червону кулю. |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||
Розв’язання. Позначимо подію – з урни витягнули червону кулю, через А. |
|
|
|
|
часу |
(по |
абсолютній |
величині), |
тт. |
y - x £1/ 3 . |
||||||||||||
|
|
|
|
3 |
||||||||||||||||||
Всього маємо n =12 куль, з них червоних m =5. Тоді, |
застосувавши формулу (1.1) |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
отримаємо |
|
|
m |
|
|
|
|
|
|
|
M |
|
|
Розв’язком останньої нерівності є смуга x - 1 £ y £ x + 1 , |
||||||||
|
|
|
|
5 |
|
|
|
|
|
|
|
|||||||||||
|
p( A) = |
= |
. |
|
|
O |
|
1 |
x |
|
|
|
|
|
|
|
3 |
3 |
||||
|
n |
|
|
|
|
|
що знаходиться в середині квадрата (площа g) (рис.1). |
|||||||||||||||
|
|
|
12 |
|
|
|
|
Рис. 1 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
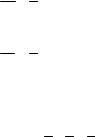
7
За формулою (1.3) маємо
|
|
|
1 - 2 × |
1 |
|
æ |
2 |
ö2 |
|
|
|
|
|
Sg |
|
|
|
×ç |
|
÷ |
|
5 |
|
||
|
|
2 |
|
3 |
|
|
||||||
p(C) = |
= |
|
|
|
è |
ø |
= |
. |
||||
SG |
|
|
12 |
|
|
|
9 |
|||||
|
|
|
|
|
|
|
|
|
||||
Площа g дорівнює площі квадрата без суми площ двох кутових не замальованих трикутників.
Елементи комбінаторики
Для підрахунку числа появи подій використовують елементи комбінаторики. Сполуки – це групи, утворені з будь - яких предметів. Предмети, з яких утво-
рені сполуки, називаються елементами. Найбільш важливими єперестановки, роз-
міщення, комбінації.
Розміщеннями з n елементів по m називають такі сполуки, кожна з яких містить m елементів, узятих з даних n елементів, і які відрізняються одна від одної або порядком елементів, або самими елементами
Am = n × |
( |
n -1 × n - 2 |
) |
×...× én - |
( |
m -1 ù = |
n! |
|
(1.4) |
|
(n - m)! |
||||||||||
n |
) ( |
ë |
)û |
|
||||||
Перестановками називаються сполуки складені із одних і тих же m різних елементів, і які відрізняються тільки порядком їх розташування. Число можливих перестановок
|
Pm = m! , |
|
(1.5) |
||
де m! = 1×2 ×...× m . Треба замітити, що 0! = 1, |
1! = 1 . |
||||
Комбінаціями називаються такі сполуки з |
n елементів по m елементів, які від- |
||||
різняються хоча б одним елементом. Число комбінацій |
|||||
Cnm = |
n! |
|
. |
(1.6) |
|
m!×(n - m)! |
|||||
|
|
|
|||
Розміщення, перестановки і комбінації зв’язані рівністю |
|||||
Am = P ×C m . |
|
(1.7) |
|||
n |
m n |
|
|
||
Приклад 1.4. В групі 25 студентів. Необхідно вибрати старосту, його замісника і профорга. Скільки існує способів це зробити?
Розв’язання. Групування по 3 чоловіки з 25 можна здійснити C253 способами. Але серед вибраних 3 - х студентів теж важливо розподілення посад, а це можна зробити P3 способами. Тому маємо задачу на розміщення
A253 = 25× 24 ×23 = 13800 (сп.)
Приклад 1.5. Потяг має 5 вагонів, які можна причепити в різному порядку. Скільки існує варіантів сформувати потяг з даної кількості вагонів.
Розв’язання. Кожний варіант формування потягу відрізняється тільки місцем розташування вагонів, тт. маємо задачу на перестановки з 5 елементів
P5 = 5! = 1×2 ×3×4 ×5 = 120 (сп.)
8
Приклад 1.6. Скількома способами можна вибрати 3 фарби з 7, що є в наявності. Розв’язання. Шукане число способів визначається комбінаціями з 7 елементів по
3 елементи. Отже,
C73 = |
7! |
= |
1×2 ×3 ×4 ×5 ×6 ×7 |
= 35 (сп.) |
|
|
|||
|
3!×(7 - 3)! 1×2 ×3×1×2 ×3 ×4 |
|
||
1.2. Теореми додавання і множення Сумою декількох подій називається подія, яка полягає в появі хоча б однієї з
даних подій.
Добутком декількох подій називається подія, яка полягає в сумісному з’явленні усіх цих подій.
Різницею А – В двох подій А і В називається подія, яка полягає в тім, що подія А відбудеться, а подія В не відбудеться.
Теорема. Ймовірність суми несумісних подій дорівнює сумі ймовірностей цих
подій:
p( A + B + ... + K ) = p( A) + p(B) +... + p(K ) . |
(1.8) |
Слідство 1. Сума ймовірностей подій, які утворюють повну групу, дорівнює |
|
одиниці: |
|
p( A) + p(B) + ... + p(K ) = 1 . |
(1.9) |
Слідство 2. Сума ймовірностей протилежних подій дорівнює одиниці: |
|
p( A) + p(B) = 1 . |
(1.10) |
Приклад 1.7. В скриньці 20 червоних, 10 синіх і 5 білих ґудзиків. Знайти ймовірність витягнути з скриньки кольоровий ґудзик.
Розв’язання. Ймовірність взяти з скриньки червоний ґудзик дорівнює (подія А)
p( A) = 20 = 4 . 35 7
Ймовірність узяти з скриньки синій ґудзик дорівнює (подія В)
p(B) = 10 = 2 . 35 7
Події А і В несумісні (поява ґудзика одного кольору виключає появу ґудзика іншого кольору), тому можна застосувати теорему додавання несумісних подій.
Шукана ймовірність за формулою (1.8) дорівнює
p( A + B) = p( A) + p(B) = 4 + 2 = 6 . 7 7 7
Приклад1.8. В порт заходять судна тільки з трьох пунктів відправлення. Ймовірність появи судна з першого пункту дорівнює 0,2, з другого пункту – 0,6. Знайти ймовірність появи судна з третього пункту.
Розв’язання. Нехай подія А – в порт заходять судна з першого пункту, подія В
– в порт заходять судна з другого пункту, подія С – в порт заходять судна з третього пункту. Отже,
p( A) + p(B) + p(C) = 1 .
9
Тоді p(C) =1 - p( A) - p(B) .
За умовою p( A) = 0, 2; p(B) = 0, 6 . Підставивши дані в формулу (1.9), отримає-
мо p(C) =1 - 0, 2 - 0, 6 = 0, 2 .
Дві події називаються незалежними, якщо поява однієї з них не змінює ймовірності появи іншої.
Декілька подій А, В, ..., L називаються незалежними в сукупності (або просто незалежними), якщо незалежні любі дві з них і незалежна люба з даних подій і любі комбінації (добутки) подій, що залишилися. В протилежному випадку події А, В, ..., L називаються залежними.
Ймовірність події В за умови, що подія А вже відбулася, називається умовною ймовірністю і позначається pA (B) або p(B / A) .
Теорема. Ймовірність сумісної появи двох залежних подій дорівнює добутку ймовірності однієї з них на умовну ймовірність іншої, обчислену в передбаченні, що перша подія відбулася
p( AB) = p( A) × pA (B) = p(B) × pB ( A) . |
(1.11) |
Теорема множення ймовірностей сумісної появи залежних подій легко узагальнюється на випадок довільного числа подій
p( ABC...KL) = p( A) × pA (B)× pAB (C )×...× pAB...K (L) , |
(1.12) |
тт. ймовірність добутку декількох сумісних залежних подій дорівнює добутку
ймовірності однієї з цих подій на умовні ймовірності інших, при цьому умовна ймовірність кожної послідуючої події обчислюється в передбаченні, що всі попередні події відбулися.
Приклад 1.9. В місті знаходиться 15 продовольчих і 5 непродовольчих крамниць. Навмання для приватизації були відібрані три крамниці. Знайти ймовірність того, що всі крамниці непродовольчі.
Розв’язання. Нехай подія А – першою відібрана для приватизації непродовольча крамниця; подія В – другою відібрана для приватизації непродовольча крамниця при умові, що подія А вже відбулася; подія С – третьою відібрана для приватизації непродовольча крамниця при умові, що події А і В вже відбулися.
Ймовірності подій А, В і С відповідно дорівнюють:
p( A) = |
5 |
, |
p |
A ( |
B = |
4 |
, |
p |
|
(C) = |
3 |
. |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
||||||||||||||||||
20 |
|
|
) 19 |
|
|
|
AB |
|
|
|
18 |
|
|
|
|
|
|
|
|
|
|||||
Застосувавши теорему множення декількох сумісних подій, тобто використав- |
|||||||||||||||||||||||||
ши формулу (1.12), матимемо |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
p( ABC) = p( A) × p |
A ( |
B × p |
|
( |
C |
= |
|
5 |
× |
4 |
× |
3 |
= |
|
1 |
. |
|||||||||
|
|
|
|
114 |
|||||||||||||||||||||
|
|
|
|
|
|
) |
|
AB |
|
) |
20 19 18 |
|
|
||||||||||||
Теорема. Ймовірність сумісної появи двох незалежних подій дорівнює добутку |
|||||||||||||||||||||||||
ймовірностей цих подій: |
p( A × B) = p (A) p (B) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1.13) |
||||||||||
Теорема множення ймовірностей сумісної появи декількох незалежних подій на |
|||||||||||||||||||||||||
випадок довільного числа подій |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
p( ABC ... KL) = p( A) × p(B) × |
... p(L) , |
|
|
|
|
|
|
|
|
|
(1.14) |
||||||||||||||
10
тт. ймовірність добутку сумісної появи декількох незалежних подій дорівнює до-
бутку ймовірностей цих подій.
Приклад 1.10. Ймовірність влучення в ціль для першого стрільця дорівнює 0,8, для другого – 0,7, для третього – 0,9. Кожний з стрільців зробив по одному пострілу. Яка ймовірність того, що в мішені три пробоїни.
Розв’язання. Позначимо події Ai – влучення в ціль i – го стрільця ( i = 1, 2,3 );
В – в мішені три пробоїни. Тоді B = A1 × A2 × A3 і події A1 , A2 , A3 – незалежні. За теоремою множення незалежних подій і формулою (1.14), маємо
p(B) = p( A1 ) × p( A2 ) × p (A3 ) = 0, 7 ×0,8 ×0,9 = 0,504 .
Теорема. Ймовірність появи хоча б однієї з подій A1 , A2 , ... , An незалежних в сукупності, дорівнює різниці між одиницею і добутком ймовірностей протилежних
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
подій A1 , A2 , ..., |
An . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
p( A) = 1- p( |
|
|
|
|
|
|
|
|
|
|
(1.15) |
|||
|
|
|
|
|
|
A1 ) × p( A2 ) × ... p( An ) |
||||||||||||||
Якщо позначити |
p( |
|
|
|
|
|
|
|||||||||||||
A1 ) = q1 , p( A2 ) = q2 , ... p( An ) = qn , то формула (1.15) матиме |
||||||||||||||||||||
вигляд |
|
|
|
p( A) = 1 - q1 ×q2 × ... ×qn . |
(1.16) |
|||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||
Слідство. |
Якщо |
події A1 , A2 , ... An мають однакову ймовірність, |
рівну p , то |
|||||||||||||||||
ймовірність появи хоча б однієї з цих подій |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
p( A) = 1- qn . |
(1.17) |
||||||||
Приклад 1.11. Ймовірність того, що при одному пострілі стрілець влучив в десятку дорівнює 0,6. Скільки пострілів повинен зробити стрілець, щоб з ймовірністю не менше 0,8 він влучив в десятку хоча б один раз?
Розв’язання. Позначимо через А – подію, що при n пострілах стрілець влучить в десятку з ймовірністю 0,8 хоча б один раз. Події, що полягають у влученні в ціль при першому, другому пострілах і т.п. незалежні в сукупності, тому можливо застосувати формулу (1.17).
Прийнявши до уваги, що за умовою p( A) ³ 0,8, p = 0,6 , отже q = 1- 0, 6 = 0, 4 , отримаємо:
1 - 0, 4n ³ 0,8 , звідки 0, 4n £ 0, 2 .
Логарифмуючи цю нерівність за основою e , отримаємо
n ×ln 0, 4 £ ln 0, 2 . |
|
|
|
|
Звідки, враховуючи, що ln 0, 4 < 0 , маємо n ³ |
ln 0, 2 |
= |
-1, 6094 |
» 1, 756 » 2 . |
ln 0, 4 |
|
|||
|
-0, 9163 |
|
||
Отже, n ³ 2 , тобто стрілець повинен зробити не менше 2 пострілів.
Приклад 1.12. Ймовірність того, що студент здасть перший іспит дорівнює 0,9; другий – 0,8; третій – 0,7. Знайти ймовірність того, що студентом будуть здані: а) тільки 2 – й іспит; б) тільки один іспит; в) тільки два іспити; г) по крайній мірі два іспити; д) хоча б один іспит.
Розв’язання. а) Розглянемо події: Ai – студент здасть i – й іспит (i =1, 2,3) ;
11
В – студент здасть тільки другий іспит з трьох. Тоді подія B = A1 × A2 × A3 , тт. сумісне здійснення трьох подій які полягають в тому, що студент здасть другий іспит і не здасть 1 – й і 3 – й іспити. Враховуючи, що події A1 , A2 , A3 незалежні і за умовою
p( A1 ) = 0, 9; p( A2 ) = 0,8; p( A3 ) = 0, 7; p( A1 ) = 0,1; p( A2 ) = 0, 2; p( A3 ) = 0,3 ,
отримаємо
p(B) = p( A1 A2 A3 ) = p( A1 ) × p( A2 ) × p( A3 ) = 0,1×0,8 ×0, 2 = 0, 016 .
б) Нехай подія С – студент здасть один іспит з трьох. Подія С відбудеться, якщо студент здасть тільки перший іспит з трьох, або тільки другий, або тільки третій, тт.
p(C) = p( A1 × A2 × A3 + A1 × A2 × A3 + A1 × A2 × A3 ) = 0, 9 ×0, 2 ×0, 3 + 0,1×0,8 ×0,3 + 0,1×0, 2 ×0, 7 = = 0, 054 + 0, 024 + 0, 014 = 0, 092 .
в) Нехай подія D – студент здасть тільки два іспити. Подія D відбудеться, якщо здійсниться наступне: студент здасть перший і другий іспити і не здасть третього; здасть перший і третій іспити і не здасть другого; здасть другий і третій іспити і не здасть першого, тт.
p(D) = p( A1 × A2 × A3 + A1 × A2 × A3 + A1 × A2 × A3 ) = 0, 9 × 0,8 ×0,3 + 0,9 ×0, 2 ×0, 7 + 0,1×0,8 ×0, 7 = = 0, 216 + 0,126 + 0, 056 = 0,398 .
г) Нехай подія Е – студент здасть по меншій мірі два іспити (інакше: “хоча б два іспити” або “не менше двох” іспитів). Подія Е означає здачу любих двох іспитів з
трьох або всіх трьох іспитів, тт. E = A1 × A2 × A3 + A1 × A2 × A3 + A1 × A2 × A3 + A1 × A2 × A3 . Отже,
p(E) = 0, 9 ×0,8 ×0,3 + 0,9 ×0, 2 ×0, 7 + 0,1×0,8 ×0, 7 + 0,9 ×0,8 ×0, 7 = 0, 216 + 0,126 + 0, 056 + +0,504 = 0, 902 .
д) Нехай подія K – студент здасть хоча б один іспит ( інакше: “не менше одного” іспиту ). Подія К являє собою суму подій C (три варіанта) і E (чотири варіанта), тт.
K = A1 + A2 + A3 = C + E (сім варіантів).
Проте простіше знайти ймовірність події К, якщо перейти до протилежної події, яка дає лише один варіант K = A1 + A2 + A3 = A1 × A2 × A3 , тт. застосувати формулу (1.15).
Отже, p(K ) = p( A1 + A2 + A3 ) = 1- p(K ) = 1- p (A1 × A2 × A3 ) = 1- p( A1 ) × p( A2 ) × p( A3 ) =
= 1- 0,1×0, 2 ×0, 3 = 0, 994 .
Теорема. Ймовірність суми двох сумісних подій дорівнює сумі ймовірностей
цих подій без ймовірності їх добутку, тт. |
|
p( A + B) = p( A) + p(B) - p( AB) . |
(1.18) |
Зауваження 1. Формула (1.18) має вигляд для незалежних подій p( A + B) = p( A) + p(B) - p( A) × p(B)
для залежних подій p( A + B) = p( A) + p(B) - p( A) × pA (B) .
Зауваження 2. Якщо події А і В несумісні, то їх суміщення є неможлива подія і, отже p( AB) = 0 . Формула (1.18) для несумісних подій прийме вигляд
p( A + B) = p( A) + p(B) .
12
Приклад 1.13. Знайти ймовірність того, що взяте навмання двохзначне число буде кратним 2 або 5 або тому і іншому одночасно.
Розв’язання. Нехай А – подія, яка відповідає тому, що двохзначне число кратне 2, а В – подія, яка відповідає кратності 5 двохзначного числа. Усього двохзначних чисел 90. Серед чисел, які кратні 2 буде 45, а кратних 5 – 18. Чисел, які кратні і 2 і 5 буде 9 (10; 20; 30; 40; 50; 60; 70; 80; 90). Отже, застосувавши теорему складання сумісних подій і враховуючи, що події А і В незалежні, за формулою (1.18), отримаємо
p( A + B) = p( A) + p(B) - p( A) × p(B) = 45 + 18 - 9 = 54 = 0, 6 . 90 90 90 90
1.3. Формула повної ймовірності. Формули Бейеса
Слідством двох основних теорем теорії ймовірностей– теореми складання і теореми множення – є формула повної ймовірності і формули Бейеса.
Теорема. Якщо подія А може настати лише при умові появи однієї з несумісних подій (гіпотез) B1 , B2 , ,..., Bn , що утворюють повну групу, то ймовірність події А до-
рівнює сумі добутків ймовірностей кожної з цих подій(гіпотез) на відповідні умовні ймовірності події А:
n |
|
p( A) = å p (Bi )× pBi (A ) |
(1.19) |
i =1
Приклад 1.14. На завод надійшли двигуни від трьох моторних заводів. Від першого заводу надійшло 10 двигунів, від другого – 6 і від третього – 4 двигуна. Ймовірності безвідмовної роботи цих двигунів на протязі гарантійного строку відповідно дорівнюють: 0,9; 0,7; 0,6. Яка ймовірність того, що встановлений на машину двигун буде працювати без дефектів на протязі гарантійного строку?
Розв’язання. Нехай А – подія, яка відповідає тому, що встановлений на машину двигун буде працювати без дефектів на протязі гарантійного строку.
Позначимо B1 , B2 , B3 події, що двигуни виготовлені відповідно на першому, другому, третьому моторних заводах. Ймовірності цих подій
p(B ) = |
10 |
= 0,5 , |
p(B ) = |
6 |
= 0, 3 , |
p(B ) = |
4 |
= 0, 2 . |
|
|
|
||||||
1 |
20 |
|
2 |
20 |
|
3 |
20 |
|
|
|
|
|
|
|
Умовні ймовірності події А отримані за умови задачі pB1 ( A) = 0,9 ; pB2 ( A) = 0, 7 ; pB3 ( A) = 0, 6 .
Тоді використавши формулу (1.19), обчислимо шукану ймовірність
3
p( A) = å p (Bi )× pBi ( A )= 0,5 ×0,9 + 0,3 ×0, 7 + 0, 2 ×0, 6 = 0, 45 + 0, 21 + 0,12 = 0, 78 .
i =1 |
|
|
|
|
|
Для визначення ймовірності події Bi |
, при умові, що подія A здійснилася, ви- |
||||
користовують формули Бейеса. |
|
|
|
|
|
pA (Bi )= |
p (Bi |
)× pBi |
(A) |
|
|
|
|
|
, |
(1.20) |
|
n |
|
|
|||
å p (Bi )× pBi (A )
i =1
де i = 1, ..., n .
13
Формули Бейеса дозволяють переоцінювати ймовірності гіпотез після того, як становиться відомим результат випробування, в якому з’являється подія А.
Приклад 1.15. До взуттєвої майстерні для ремонту приносять чоботи і туфлі у співвідношенні 2:3. Ймовірність якісного ремонтування чобіт дорівнює 0,9, а туфель – 0,85. Проведена перевірка якості однієї пари взуття. Виявилося, що ця пара взуття відремонтована якісно. Яка ймовірність того, що це: а) чоботи; б) туфлі.
Розв’язання. Нехай подія А – принесене взуття відремонтовано якісно. Позна-
чимо подію B1 – до ремонту принесли чоботи, |
B2 |
– до ремонту принесли туфлі. |
||||||||||||||
Отже, ймовірності гіпотез |
p(B ) |
= |
2 |
= 0, 4 , |
p(B ) = |
3 |
= 0, 6 . |
|||||||||
|
|
|||||||||||||||
|
|
|
1 |
5 |
|
|
2 |
5 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Умовні ймовірності відповідно дорівнюють |
|
|
|
|
|
|
|
|||||||||
Тоді: |
|
|
pB1 |
( A) = 0,9 ; |
pB2 |
( A) = 0,85 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а) ймовірність того, що відремонтованим якісно взуттям є чоботи буде |
||||||||||||||||
p |
A ( |
B |
= |
|
0, 4 ×0, 9 |
|
= |
0,36 |
» 0, 41 ; |
|||||||
0, 4 ×0, 9 + 0, 6 ×0,85 |
|
|
||||||||||||||
|
1 |
) |
0,87 |
|
|
|||||||||||
б) ймовірність того, що відремонтованим якісно взуттям є туфлі буде |
||||||||||||||||
p |
A ( |
B |
= |
|
0, 6 ×0,85 |
|
= |
0,52 |
» 0,59 . |
|||||||
0, 4 ×0,9 + 0, 6 ×0,85 |
|
|||||||||||||||
|
2 |
) |
0,87 |
|
|
|||||||||||
1.4. Повторення випробувань
Якщо ймовірність появи події А в кожному випробуванні не змінюється в залежності від результатів інших, то такі випробування називаються незалежними відносно події А. Якщо незалежні повторні випробування проводяться при одному й тому ж комплексі умов, то ймовірність появи події А в кожному випробуванні одна й та ж.
Така послідовність незалежних випробувань отримала назву схеми Бернуллі. Формула Бернуллі. Ймовірність того, що в n незалежних випробуваннях, у
кожнім з яких ймовірність події дорівнює p (0 < p < 1) , подія з’явиться рівно k разів (байдуже в якій послідовності) дорівнює:
|
Pn (k )= Cnk × pk ×qn-k = |
|
n! |
|
× pk × qn-k , |
(1.21) |
|
|
k !(n - k )! |
||||
|
|
|
|
|
||
де q =1 - p . |
|
|
|
|
|
|
Ця формула відображує біномний розподіл ймовірностей. |
|
|||||
Якщо |
отримані ймовірності |
зобразити |
графічно точками |
з координатами |
||
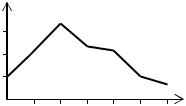
(k, Pn (k )) , то з’єднуючи ці точки отримаємо многокутник або полігон розподілу ймо-
вірностей (рис.2). Використовуючи многокутник розподілу можна стверджувати, що існують такі значення m при яких ймовірність Pn (k ) буде найбільшою. Число k0 по-
яви події А в n незалежних випробуваннях називаєтьсянайімовірнішим, якщо ймовірність здійснення цієї події Pn (k ) при любім k .
Найімовірніше число k0 визначається з подвійної нерівності:
14 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
np - q £ k0 < np + p , |
(1.22) |
|||
Pn (k ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
причому: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а) якщо число np - q –дрібне, то існує од- |
||
0, 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
не найімовірніше число k0 ; |
|
0, 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
б) якщо число np - q – ціле, то існує два |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
0,1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
найімовірніших числа, а саме k0 |
і k0 +1 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
в) якщо число np – ціле, то найімовірніше |
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
число k0 = np . |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис.2 |
|
|
|
|
|
|
|
|
|
|
Приклад 1.16. Батарея зробила 14 пострілів по об’єкту, ймовірність влучень в який при кожному пострілі дорівнює0,2. Знайти найімовірніше число влучень і ймо-
вірність цього числа влучень. |
|
Розв’язання. За умовою p = 0, 2 , |
тоді q =1 - p = 0,8 , n = 14 . Використавши |
формулу (1.22), отримаємо |
|
14 ×0, 2 - 0,8 £ k0 < 14 ×0, 2 + 0,8 |
|
2 £ k0 |
< 3, 6 . |
Оскільки число np - q = 2 – ціле, то існує два найімовірніших числа k0 = 2 і
k0 +1 = 3 .
Тепер використавши формулу (1.21) обчислимо ймовірність числа влучень
P |
( |
2 |
) |
= C 2 |
×0, 22 ×0,812 = |
14! |
|
×0, 04 ×0,812 = 0, 25 ; |
||
|
|
|||||||||
14 |
|
|
|
14 |
|
2!×12! |
|
|||
|
|
|
|
|
|
|
|
|
||
P |
( |
3 |
) |
= C3 |
×0, 23 ×0,811 = |
14! |
|
×0, 23 ×0,811 = 0, 25 . |
||
|
|
|||||||||
14 |
|
14 |
|
3!×11! |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
Увипадку, коли n велике, а p мале (так згідно з [3] p < 0,1 ; npq £ 9 , а згідно з
[1]l = np £ 10 ) маємо справу з рідкісними масовими явищами, замість формули (1.21) користуються наближеною формулою Пуассона:
P (k) = |
lk ×e-l |
|
|
(1.22) |
|
|
||
n |
k ! |
|
|
||
Приклад 1.17. В новому мікрорайоні поставлено 10000 кодових замків на вхідних дверях будинків. Ймовірність виходу зі строю одного замка на протязі місяця дорівнює 0,0002. Знайти ймовірність того, що за місяць підкажуть три замка.
Розв’язання. За умовою n = 10000 , k = 3 , p = 0, 0002 . l = np = 10000 ×0, 0002 = 2
l = 2 £ 10 , отже, можна примінити формулу Пуассона (1.22)
P |
( |
3 |
) |
= |
23 |
×e-2 » 0,18 . |
|
||||||
10000 |
|
3! |
|
|||
Користуватися формулою Бернуллі при великих значеннях n достатньо важко, оскільки формула потребує виконання дій над громіздкими числами. Тому для набли-
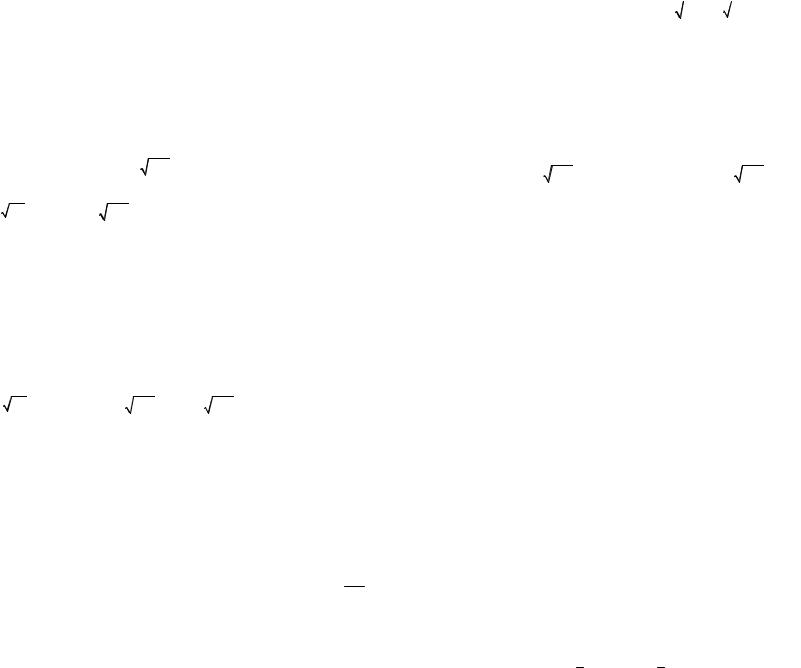
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15 |
женого (асимптотичного) обчислення ймовірностей |
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Pn (k ) = Cnk × pk qn-k |
|
|
|
|
k2 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
і Pn (k1 , k2 ) = å Pn (k ) |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k =k1 |
|
|
|
в n незалежних випробуваннях Бернуллі при великих n , k , |
k1 , |
k2 |
використовують |
||||||||||||||||||||||||||||||
теореми Муавра-Лапласа. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Локальна теорема Муавра-Лапласа |
|
|
|
||||||||||||||||||
Якщо ймовірність |
p появи події |
A в кожнім іспиті стала і відмінна від нуля і |
|||||||||||||||||||||||||||||||
одиниці, то ймовірність |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Pn (k ); |
1 |
|
|
×j (x ), |
|
|
(1.23) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
npq |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
де j (x )= |
|
|
1 |
|
|
×e- |
x2 |
|
і x = |
k |
- np |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
2p |
|
|
|
|
|
|
|
|
|
|
npq |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Функція |
|
|
j (x) – |
парна |
(j (-x) = j (x)) , монотонно |
спадна (при x ® ¥, |
|||||||||||||||||||||||||||
j (x) ® 0 ) і обчислюється за таблицею1 (Додаток 1). |
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Інтегральна теорема Муавра-Лапласа |
|
|
|||||||||||||||||||
Якщо ймовірність |
p появи події A в кожному іспиті стала і відмінна від нуля і |
||||||||||||||||||||||||||||||||
одиниці, то ймовірність Pn (k1 , k2 ) того, |
що подія A з’явиться в |
n |
іспитах від k1 до |
||||||||||||||||||||||||||||||
k2 разів, наближено дорівнює |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
Pn (k1 , k2 ) ; Ф (x2 ) -Ф (x1 ) , |
|
|
(1.24) |
|||||||||||||||||||
де Ф (x )= 1 |
|
|
x |
- |
z2 |
x2 = k2 - np , |
x1 = k1 - np . |
|
|
|
|||||||||||||||||||||||
|
|
e |
2 |
|
dz і |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
ò0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
2p |
|
|
|
|
|
|
|
|
|
|
npq |
npq |
|
|
|
||||||||||||||
Функція Лапласа Ф( x ) – непарна (Ф(- x ))= – Ф( x ), монотонно зростаюча (при x ® ¥ , Ф (x) ® 1 ) і обчислюється за таблицею додатку 2.
Наближені формули Муавра-Лапласа застосовують практично у випадках коли p і q не малі а npq ³ 20 [1]. При цій умові формули (1.23) і (1.24) дають незначні по-
хибки обчислення ймовірностей.
Приклад 1.18. В деякій місцевості на кожні 100 сімей припадає 80 холодильників. Знайти ймовірність того, що з 400 сімей: а) 300 сімей мають холодильники; б) від 320 до 350 сімей (включно) мають холодильники.
Розв’язання. Ймовірність того, що сім’я має холодильник p = 80 = 0,8 . Пере100
віримо умову застосування формул (1.23) і (1.24.)
n = 400 , p = 0,8 , q = 0, 2 , тоді n × p × q = 400 ×0,8 ×0, 2 = 64 ³ 20 .
Отже, теоремами Муавра-Лапласа можна користуватися.
а) Скориставшись локальною теоремою Муавра-Лапласа. Спочатку визначимо x , враховуючи, що n = 400 , k = 200 , p = 0,8 , q = 0, 2 , тоді
16
x = |
k |
- np |
|
= |
300 - 400 |
×0,8 |
|
= |
20 |
= -2, 5 |
|
|
|
|
|
|
|
|
|
||||
|
|
npq |
400 ×0,8 |
×0, 2 |
8 |
|
|||||
Користуючись додатком 1 позначенню x = -2,5 знайдемо j (-2,5), врахувавши пар-
ність j (-2,5) = j (2, 5) = 0, 0175 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Отже, за формулою (1.23) маємо: P |
300 |
» |
0,0175 |
» 0, 0022 . |
|||||||||||||||
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
400 ( |
|
|
) |
|
|
|
|
|
||||
|
б) За умовою n = 400 , k1 |
= 320 , k2 = 350 , |
8 |
|
|
|
|
|||||||||||||
|
p = 0,8 , |
q = 0, 2 . |
||||||||||||||||||
|
Визначимо x1 і x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
x = |
k1 |
- np |
|
= |
320 - 400 ×0,8 |
= 0 , |
x |
= |
k2 |
- np |
|
= |
350 - 400 ×0,8 |
= |
30 |
= 3, 75 |
||||
|
|
|
|
|
|
|
|
|||||||||||||
1 |
|
npq |
8 |
|
2 |
|
|
npq |
|
|
8 |
8 |
|
|||||||
|
|
|
|
|
|
|
|
|
||||||||||||
Ф(0)=0, Ф(3,75)=0,499890005-0 » 0,5
Отже, за формулою (1.24) маємо
P400 (320,350) ; 0, 499890005 - 0 » 0,5 .
1.5. Випадкові величини Випадковою величиною називають таку змінну величину, яка у результаті ви-
пробування може набувати одного з можливих значень, причому заздалегідь невідомо якого.
Дискретною (перервною) називається випадкова величина, яка набуває окремі, ізольовані можливі значення з визначеними ймовірностями.
Неперервною називається випадкова величина, нескінченна множина значень якої є деякий інтервал (кінцевий або нескінчений) числової осі.
Законом розподілу випадкової величини називається всяке співвідношення, яке встановлює зв’язок між можливими значеннями випадкової величини і їхніми ймовірностями.
1.5.1. Дискретні випадкові величини і їх числові характеристики
Найпростішою формою завдання закону розподілу дискретної випадкової величини Х є таблиця (матриця), в якій перелічувані в порядку зростання всі можливі значення випадкової величини і відповідні їм ймовірності
Х: |
x1 |
x2 |
... |
xi |
... |
xn |
|
p1 |
p2 |
... |
pi |
... |
pn |
Така таблиця називається рядом розподілу дискретної випадкової величини.
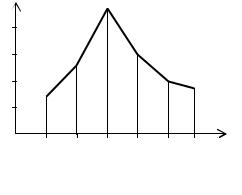
Ряд розподілу може бути зображений графічно, якщо по осі абсцис відкладати значення випадкової величини, а по осі ординат – відповідні їм ймовірності. З’єднання отриманих точок утворює ломану, яка називається многокутником або полігоном
розподілу ймовірностей.
Приклад 1.19. Гральну кістку кинули 3 рази. Написати закон розподілу числа з’явлення шістки.
Розв’язання. За умовою
p = 1 , q =1 - p = 5 , n = 3 .
6 |
6 |
17
pi
0 |
x1 |
x2 ... |
xi |
... |
xn |
x |
|
|
|
|
|
|
|
Рис.3
Закон розподілу числа з’явлення шістки відповідає біномному розподілу
P |
(0 )= C0 |
× p0 ×q3 |
=1× |
æ 1 ö0 |
× |
æ 5 ö3 |
|
= |
125 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
ç |
|
÷ |
|
ç |
|
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
3 |
3 |
|
|
|
|
|
|
|
|
|
|
216 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
è |
6 ø |
|
|
è |
6 ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
1 |
|
1 |
|
2 |
æ 1 ö æ 5 ö2 |
|
1 |
|
|
25 |
|
|
|
25 |
|
|
|
75 |
||||||||||||||||
P3 (1 )= C3 |
|
× p |
×q |
|
= 3×ç |
|
÷× |
ç |
|
÷ = |
|
|
|
× |
|
|
|
|
= |
|
|
= |
|
|
|
||||||||||
|
|
|
6 |
|
|
|
|
|
|
|
72 |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
è 6 ø |
è |
ø |
|
|
|
2 36 |
|
|
|
216 |
||||||||||||||||||
P |
(2 )= C |
2 |
× p2 × q1 |
= 3 ×æ |
1 |
ö2 |
×æ |
5 |
ö |
= 3× |
1 |
|
× |
5 |
= |
15 |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
3 |
3 |
|
|
|
|
|
ç |
÷ |
|
|
ç |
÷ |
|
|
|
|
|
36 |
6 |
|
216 |
|
|||||||||||||
|
|
|
|
|
|
|
|
è |
6 ø |
|
|
è |
6 ø |
|
|
|
|
|
|
|
|||||||||||||||
P |
(3 )= C3 |
|
× p3 ×q0 |
=1× |
æ 1 ö3 |
|
× |
æ 5 ö0 |
= |
1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
ç |
|
÷ |
|
ç |
÷ |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
3 |
3 |
|
|
|
|
|
|
|
|
|
|
|
216 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
è |
|
6 ø |
|
|
è |
6 ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Х: |
Тоді |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
1 |
|
2 |
|
3 |
|
||||
|
|
125 |
|
|
75 |
|
|
15 |
|
|
1 |
|
|
|
216 |
|
216 |
|
216 |
|
216 |
|
|||
Закон розподілу цілком характеризує дискретну випадкову величину. Але часто закон розподілу буває невідомим або незручним для аналізу і тому приходитьсяоб межуватися меншими відомостями. Іноді вигідніше користуватися числами, які описують випадкову величину сумарно.
Числа, які призвані у стислій формі відтворювати найбільш характерні риси розподілу називаються числовими характеристиками випадкової величини.
Незважаючи на те, що сама величина Х – випадкова, її числові характеристики є величинами не випадковими, сталими.
Математичним сподіванням або середнім значенням M (X ) дискретної ви-
падкової величини Х називається сума добутків усіх її значень на відповідні їм ймовірності
n |
|
M (X )= åxi × pi . |
(1.25) |
i =1
18
Властивості математичного сподівання
1. Математичне сподівання сталої величини дорівнює самій сталій:
M(C ) = C
2.Сталий множник можна виносити за знак математичного сподівання:
M(kX ) = kM (X )
3.Математичне сподівання алгебраїчної суми кінцевого числа випадкових величин дорівнює тій же сумі їх математичних сподівань:
M(X ±Y ) = M (X ) ± M (Y )
4.Математичне сподівання добутку кінцевого числа незалежних випадкових величин дорівнює добутку їх математичних сподівань
M(XY ) = M (X )×M (Y )
5.Якщо всі значення випадкової величини збільшити (зменшити) на сталу С, то на цю ж сталу збільшиться(зменшиться) математичне сподівання цієї випадкової величини:
M(X ± C ) = M (X ) ± C
6.Математичне сподівання відхилення випадкової величини від її математичного сподівання дорівнює нулю:
MéX - M (X )ù = 0 . ë û
Дисперсією D ( X ) випадкової величини Х називається математичне споді-
вання квадрата її відхилення від математичного сподівання
D (X )= M é X - M (X |
)ù2 |
(1.26) |
ë |
û |
|
або |
|
|
D ( X )= M (X - a )2 , |
|
(1.26′) |
де a = M (X ) .
Властивості дисперсії
1. Дисперсія сталої величини дорівнює нулю:
D (C ) = 0
2. Сталий множник можна виносити за знак дисперсії, підносячи його до квад-
рата:
D (kX ) = k 2 × D (X )
3. Дисперсія випадкової величини дорівнює різниці між математичним сподіванням квадрата випадкової величини і квадратом її математичного сподівання:
D (X )= M |
( |
X 2 |
) |
- éM (X |
)ù2 |
(1.27) |
|
|
ë |
û |
|
4. Дисперсія алгебраїчної суми кінцевого числа незалежних випадкових величин дорівнює сумі їх дисперсій:
D ( X ±Y ) = D (X )+ D (Y )
19
5. Дисперсія числа появи події A в n незалежних випробуваннях, в кожнім з яких ймовірність p появи події стала, дорівнює добутку числа випробувань на ймовірність появи і не появи події в одному випробуванні:
D ( X ) = npq .
Дисперсія D ( X ) має розмір квадрата випадкової величини, що не завжди зру-
чно. Тому показником розсіювання використовують також величину 
 D ( X ).
D ( X ).
Середнім квадратичним відхиленням (стандартним відхиленням або стан-
дартом) d (X ) випадкової величини Х називається арифметичне значення кореня квадратного з її дисперсії
|
|
|
|
s ( X )= D (X ) |
(1.28) |
||
Приклад 1.20. На шляху руху автомобіля чотири світлофори. Кожний з них з ймовірністю 0,5 або дозволяє, або забороняє автомобілю подальший рух. Побудувати многокутник розподілу ймовірностей випадкової величини, що відображує число світлофорів, які автомобіль пройде без зупинки. Чому дорівнюють математичне сподівання і дисперсія випадкової величини.
Розв’язання. Нехай випадкова величина Х – число світлофорів, які пройде автомобіль без зупинки. Ця величина може приймати наступні значення: x1 = 0 , x2 = 1,
x3 = 2 , x4 = 3 , x5 = 4 .Ймовірність pi = P (X = xi ) того, що число пройдених світло-
форів Х буде дорівнювати кожному його частинному значенню, обчислюється за формулою:
ïì p ×(1- p)i -1 , i =1,..4 |
||
pi = P (X = xi ) = í |
,i = |
5 |
ï(1- p)4 |
||
î |
|
|
де p – ймовірність того, що автомо-
біль буде затриманий даним світлофором ( p = 0,5 ). За результатами обчис-
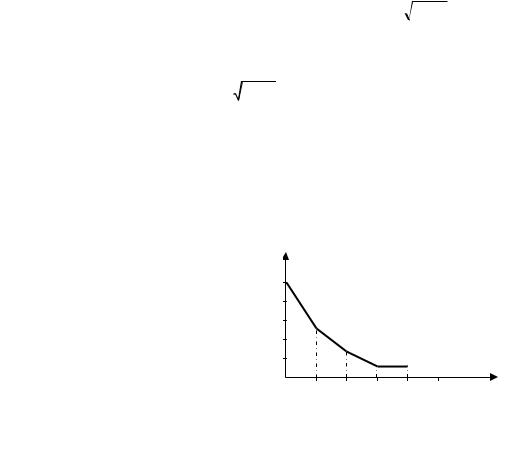
лень: p1 = 0, 5 ; p2 = 0, 25 ; p3 = 0,125 ; p4 = 0, 0625 ; p5 = 0, 0625 .
pi
0, 5 0, 4 0, 3 0, 2 0,1
0 |
1 |
2 |
3 |
4 |
5 |
xi |
Рис. 4
По цим даним будуємо многокутник розподілу ймовірностей (рис. 4). Знайдемо математичне сподівання випадкової величини по її закону розподілу
Х: |
xi |
0 |
1 |
2 |
3 |
4 |
|
||||||
|
|
|
|
|
|
|
|
pi |
0,5 |
0,25 |
0,125 |
0,0625 |
0,0625 |
Тоді використавши формулу (1.25), отримаємо:
M (X ) = 0 ×0,5 +1×0, 25 + 2 ×0,125 + 3×0,0625 + 4 ×0, 0625 = 0, 9375 .
20
Для визначення дисперсії дискретної випадкової величини визначимо спочатку M (X 2 ), для чого складемо таблицю.
Х2: |
|
2 |
0 |
1 |
4 |
|
9 |
16 |
|
|
|
xi |
|
|
|||||
|
|
pi |
0,5 |
0,25 |
0,125 |
|
0,0625 |
0,0625 |
|
|
|
M (X 2 ) = 0 ×0,5 +1×0, 25 + 4 ×0,125 + 9 ×0, 0625 +16 ×0, 0625 = 2,3125 . |
|||||||
|
Тоді за формулою (1.27) матимемо |
|
|
|
|
|
|||
|
|
|
D ( X )= 2,3125 - (0,9375)2 |
» 1, 4336 . |
|
|
|||
1.52. Неперервні випадкові величини і їх числові характеристики Функцією розподілу (інтегральною функцією розподілу або інтегральним
законом розподілу) випадкової величини Х називається функція F (x), яка визначає
для кожного значення х ймовірність того, що випадкова величина Х набуде значення менші від числа х:
|
|
|
|
F (x) = P (X < x) . |
|
(1.29) |
|||
|
Приклад 1.21. Дано ряд розподілу випадкової величини |
||||||||
Х: |
|
|
|
|
|
|
|
|
|
|
xi |
1 |
|
4 |
|
5 |
7 |
|
|
|
|
pi |
0,3 |
|
0,2 |
|
0,4 |
0,1 |
|
Знайти і зобразити графічно її функцію розподілу.
Розв’язання. Будемо задавати різні значення х і знаходити для них
F (x) = P (X < x)
1. |
Якщо x £1 , то F (x) = 0 (в тому числі і при x = 1 F (1) = P (x < 1) = 0 ). |
|
2. |
Нехай 1 < x £ 4 (наприклад, |
x = 2 ); F (x) = P (X = 1) = 0, 3 . Очевидно, що й |
F (4) = P (X < 4) = 0,3 . |
|
|
3. |
Нехай 4 < x £ 5 (наприклад, |
x = 4, 25 ); |
F (x) = P (X < x) = P (X = 1)+ P (X = 4) = 0,3 + 0, 2 = 0,5 . Очевидно, що й F (5) = 0,5 .
4. |
Нехай 5 < x £ 7 . F (x) = éP (X = 1)+ P (X = 4)ù + P (X = 5) = 0, 5 + 0, 4 = 0, 9 . |
|
|
ë |
û |
Очевидно, що й F (7) = 0, 9 . |
|
|
5. |
Нехай x > 7 . |
|
F (x) = éP (X = 1)+ P (X = 4)+ P (X = 5)ù + P (X = 7) = 0,9 + 0,1 = 1 |
||
ë |
|
û |
Отже,
