Силы трения и закон распределения скоростей при ламинарном и турбулентном режимах движения жидкости.

Рассмотрим ламинарный режим движения в цилиндрической трубе (рис. 32). В модели такое движение можно представить состоящим из множества телескопически выдвинутых цилиндров толщиной . Огибающую этих цилиндров можно рассматривать как эпюру скоростей струек.

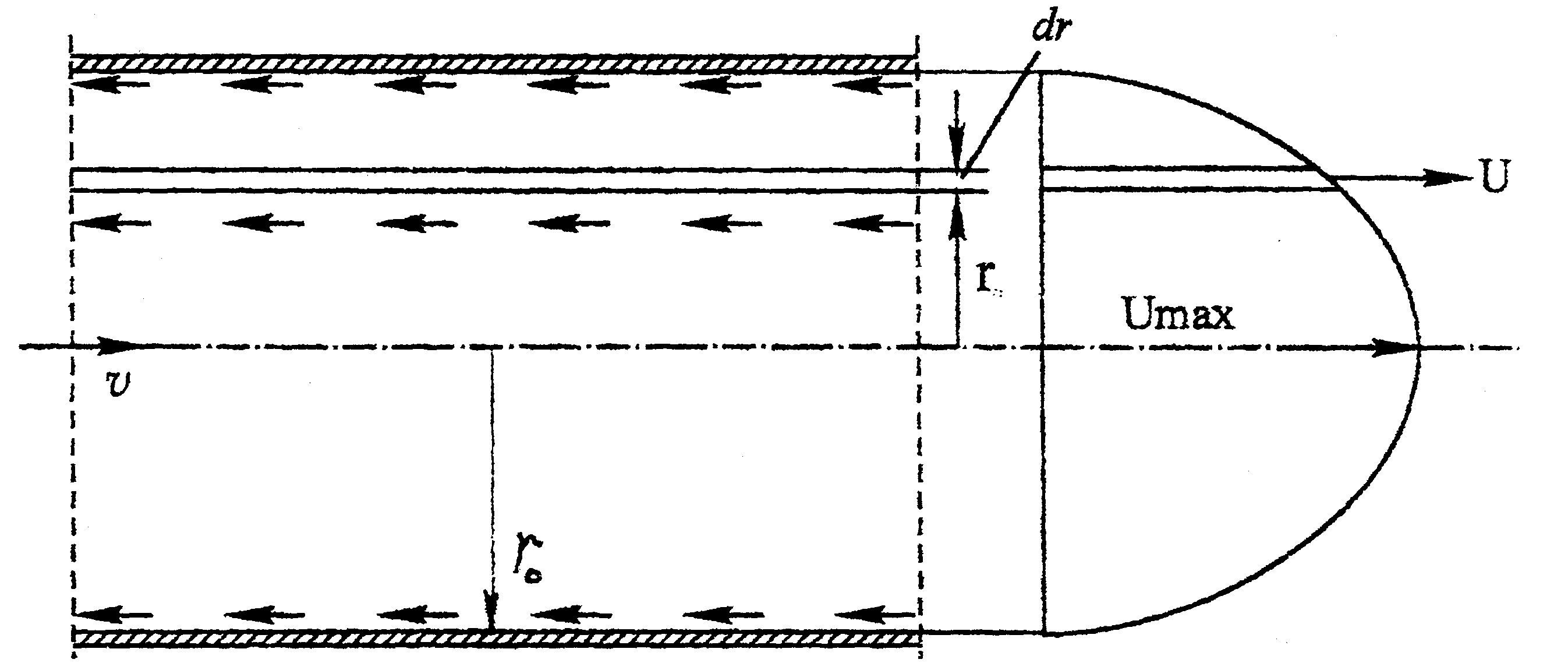
Рис. 32. Эпюры скоростей при ламинарном режиме движения

Выделим в потоке «цилиндр» . При движении этот «цилиндр» будет испытывать подтормаживающее действие со стороны «цилиндров» с большим радиусом и вовлекать их в движение.

Так как движение равномерное, гидравлический уклон

В соответствии с законом о вязкостном трении жидкостей (закон И. Ньютона), касательные напряжения

, а

Знак «минус» в формулах принят потому, что функция убывающая.

Из последней формулы определяется скорость

,

где - гидравлический радиус.

.

Интегрируя это выражение по всей площади живого сечения, т.е. в пределах от дополучим расход в этом сечении

, (88)

Для случая равномерного движения, когда .

С учетом этого формула (88) может быть преобразована к виду:

, (88, а)

В таком виде эта формула была получена в 1840 году доктором медицины Пуазейлем по результатам его экспериментальных исследований движения жидкости в капиллярных трубках и названа именем этого ученого.

Средняя скорость в живом сечении и таким образом

, (89)

Из сравнения формул ______ и (89) следует, что

, (90)

Потери напора по длине при равномерном движении в цилиндрической трубе могут быть определены из формулы 89.

С учетом того, что ;, а все потери напора принято выражать в долях скоростного напора.

, (91).

Турбулентный режим – наиболее распространенный режим движения жидкости. Несмотря на это, до настоящего времени не создано достаточно удовлетворительной теории турбулентного режима движения, основанной на уравнениях гидродинамики и которая подтверждалась бы результатами экспериментальных исследований.

Главным образом турбулентный режим движения изучается экспериментально. Факторами, характеризующими турбулентный режим движения, являются следующие:

1. Перемешивание частиц жидкости по живому сечению потока.

При турбулентном режиме частицы совершают движение не только вдоль оси, но и поперек потока. Происходит столкновение частиц, имеющих различную кинетическую энергию. Торможение частиц у стенок русла приводит к образованию вихрей, которые увлекаются потоком. Столкновение вихрей приводит к их дроблению на более мелкие вихри.

Все это приводит к перемешиванию частиц. Интенсивность перемешивания в сечении потока не одинакова: вблизи стенок русла она наименьшая, а на оси потока - наибольшая. На интенсивность перемешивания влияет вязкость жидкости. Чем больше вязкость, тем больше образуется вихрей и тем больше перемешивание.

2. Пульсация скоростей в точках. В результате столкновения частиц, вызванных перемешиванием, непрерывно изменяется их скорость движения. Следствием этого является пульсация скоростей в точках. Явление пульсации заключается в том, что мгновенная местная скорость в точках, непрерывно изменяясь во времени, колеблется около некоторой постоянной величины, называемойместной осредненной скоростью.

Опыты показывают, что за достаточно длительный период времени местная осредненная скорость остается постоянной не только по величине, но и по направлению, совпадающему с осью потока.

С введением понятия местной осредненной скорости основные понятия струйчатой модели движения (линии тока, трубка тока, элементарная струйка) можно условно распространять и на потоки с турбулентным режимом движения. Сами же такие потоки можно рассматривать как условно параллельноструйчатые и к ним можно применять уравнение Д. Бернулли.