
Физика / Физика / Механика. Лекции / lekcii_meh / glava3
.pdf
Глава 3
Работа и энергия
§ 9
Энергия, работа, мощность
Энергия – универсальная мера различных форм движения и взаимодейст-
вия. С различными формами движения материи связаны различные формы энер-
гии: механическая, тепловая, электромагнитная, ядерная и др. В одних явлениях форма движения материи не изменяется (например, горячее тело нагревает хо-
лодное), в других – переходит в иную форму (например, в результате трения ме-
ханическое движение превращается в тепловое). Однако существенно, что во всех случаях энергия, отданная (в той или иной форме) одним телом другому телу,
равна энергии, полученной последним телом.
Изменение механического движения тела вызывается силами, действующи-
ми на тело со стороны других тел. Чтобы количественно характеризовать процесс обмена энергией между взаимодействующими телами, в механике вводится поня-
тие работы силы.
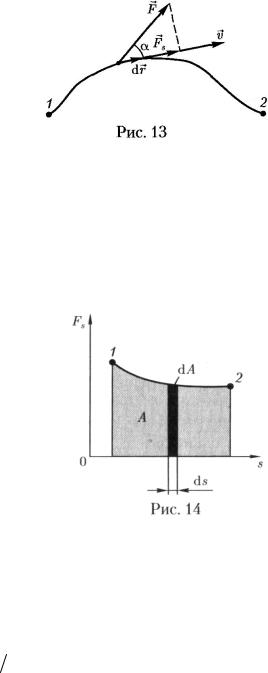
Если тело движется прямолинейно и на него действует постоянная сила F ,
которая составляет некоторый угол α с направлением перемещения s , то работа этой силы равна скалярному произведению векторов F и s или произведению
проекции силы Fs на направление вектора перемещения |
(Fs = Fscos α), умно- |
женной на перемещение точки приложения силы |
|
R |
(9.1) |
A = Fs = Fss = Fscos α. |
В общем случае сила может изменяться как по модулю, так и по направле-
нию, поэтому формулой (9.1) пользоваться нельзя. Если, однако, рассмотреть эле-
ментарное перемещение dr , то силу F можно считать постоянной, а движение точки ее приложения – прямолинейным.
Элементарной работой силы F на перемещение dr называется скалярная вели-
чина
R |
= F cos αDS = FSDS, |
|
|
|
|
|
DA = FDR |
|
|
|
|
|
|
где α – угол между векторами F |
и dr ; ds = |
|
R |
|
– |
|
|
|
|||||
|
dr |
|
||||
элементарный путь; Fs – проекция вектора F на
R
вектор dr (рис. 13).
Работа силы на участке траектории от точки 1 до точки 2 равна алгебраиче-
ской сумме элементарных работ на отдельных бесконечно малых участках пути.
Эта сумма приведена к интегралу
2 |
2 |
|
A = ∫Fdscos α = ∫Fsds . |
(9.2) |
|
1 |
1 |
|
Для |
вычисления этого |
интеграла надо знать |
зависимость силы Fs от пути s вдоль траектории 1–2.
Пусть эта зависимость представлена графически (рис.
14), тогда искомая работа A определяется на графике площадью заштрихованной фигуры. Если, например,
тело |
движется прямолинейно, |
сила F = const и |
|
α = const , то получим |
|
|
|
|
2 |
2 |
|
A = ∫Fdscos α = Fcosα∫ds = Fscosα , |
|||
|
1 |
1 |
|
где s – |
пройденный телом путь. |
|
|
Из формулы (9.1) |
следует, |
что при α < π 2 A > 0 , в этом случае состав- |
|
ляющая Fs совпадает по направлению с вектором скорости v (рис.13). Если
α > π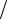 2 , то A < 0 . При α = π
2 , то A < 0 . При α = π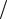 2 A = 0 .
2 A = 0 .
[A] = [Дж] = [Н × м]
Чтобы охарактеризовать скорость совершения работы, вводят понятие
мощности
N = |
dA |
. |
(9.3) |
|
dt

R
За время dt сила F совершает работу Fdr , и мощность, развиваемая этой силой в данный момент времени
|
R |
R R |
|
|
Fdr |
|
|
N = |
|
= F × v , |
(9.4) |
|
dt
т.е. равна скалярному произведению вектора силы на вектор скорости, с которой движется точка приложения этой силы; N – величина скалярная.
[N] =[Вт] (1 Вт =1 Дж/с)
Задача 1. Частица совершила перемещение по некоторой траектории в
плоскости xy из точки А с радиусом-вектором R1 = + 2 (м) в точку В с радиу- r i j
сом-вектором R2 = 2 - 3 (м). При этом на нее действовала постоянная сила r i j
F = 3i + 4j (H). Найдите работу, которую совершила эта сила.
Решение. По определению работа постоянной силы равна
|
|
|
R |
A = F × Dr , |
|||
R |
R |
R |
– вектор перемещения частицы, который равен |
где r |
= r2 |
− r1 |
|
|
R |
|
-1) + j(-3 - 2) = i - 5j . |
Dr = i (2 |
|||
Теперь подставим значения для векторов силы и перемещения в формулу работы
A = 3×1+ 4 ×(-5) = -17 Дж.
Задача 2. Тело массой m бросили под углом a к горизонту с начальной скоростью v0 . Найдите мгновенную мощность, развиваемую силой тяжести, как функцию времени.
Решение. По определению мгновенная мощность
равна
= × R
N F v .
Как видно из рисунка, сила тяжести направлена вертикально вниз, и для нее в векторном виде можно записать следующее выражение
F = -mgj .
Вектор скорости можно представить следующим образом
R = +
v vxi vy j ,
где vx = v0x = v0 cos α, vy = v0y −gt = v0 sin α −gt . С учетом этого выражение для
вектора скорости будет иметь вид
R = a + a -
v i v0 cos j (v0 sin gt ) .
Подставим выражения для векторов силы и скорости в формулу для мгновенной мощности
N = (-mgj) ×(iv0 cos a + (v0 sin a - gt)j) = mg(gt - v0 sin a) .
§ 10
Кинетическая и потенциальная энергии
Кинетическая энергия механической системы – это энергия механическо-
го движения этой системы.
Сила F , действующая на покоящееся тело и вызывая его движение, совер-
шает работу, а энергия движущегося тела возрастает на величину затраченной ра-
боты. Таким образом, работа dA силы F на пути, который тело прошло за время возрастания скорости от 0 до v, идет на увеличение кинетической энергии dT
тела, т.е.
dA = dT .
|
|
|
|
|
|
R |
R |
||
|
|
|
|
|
|
dv |
|
||
Используя II закон Ньютона F = m |
и умножая обе части равенства на |
||||||||
|
|||||||||
|
|
|
|
|
|
|
dt |
||
|
|
|
|
R |
получим |
|
|
||
перемещение dr , |
|
|
|||||||
R R |
|
|
|
R |
|
|
|
|
|
= m |
dv |
R |
= dA. |
|
|
||||
Fdr |
|
|
dr |
|
|
||||
|
dt |
|
|
||||||
|
|
|
|
|
|
|
|
||
|
|
R |
|
|
|
|
|
|
|
R |
= |
dr |
|
|
|
|
|
|
|
Так как, v |
|
|
, то |
|
|
|
|||
dt |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
||
|
|
R |
|
R |
= mvdv = dT , |
|
|
||
dA = mvdv |
|
|
|||||||
откуда
v |
mv |
2 |
|
T = ∫ mvdv = |
|
. |
|
2 |
|
||
0 |
|
|
|
|
|
|
Таким образом, тело массой m , движущееся со скоростью v, обладает кинетиче-
ской энергией
T = |
mv2 |
. |
(10.1) |
|
|||
2 |
|
|
|
Из формулы (10.1) видно, что кинетическая энергия зависит только от мас-
сы и скорости тела, т.е. кинетическая энергия системы есть функция состояния ее движения.
При выводе формулы (10.1) предполагалось, что движение рассматривается в инерциальной системе отсчета, так как иначе нельзя было бы использовать за-
коны Ньютона. В разных инерциальных системах отсчета, движущихся друг от-
носительно друга, скорость тела, а, следовательно, и его кинетическая энергия будут неодинаковы. Таким образом, кинетическая энергия зависит от выбора сис-
темы отсчета.
Потенциальная энергия – механическая энергия системы тел, определяе-
мая их взаимным расположением и характером сил взаимодействия между ними.
Если работа, совершаемая действующей силой при перемещении тела из одного положения в другое, не зависит от того, по какой траектории это переме-
щение произошло, а зависит только от начального и конечного положения, то та-
кую силу называют консервативной, а силовое поле потенциальным (сила уп-
ругости, сила Кулона, гравитационные силы).
Если работа, совершаемая силой, зависит от траектории перемещения тела из одной точки в другую, то такая сила называется диссипативной (сила трения).
Тело, находясь в потенциальном поле сил, обладает потенциальной энерги-
ей U (потенциальную энергию можно обозначить еще буквой Π ). Работа кон-
сервативных сил при элементарном изменении конфигурации системы равна приращению потенциальной энергии, взятой со знаком минус, так как, работа со-
вершается за счет убыли потенциальной энергии
dA = −dU . |
(10.2) |
Работа dA выражается как скалярное произведение силы F на перемеще- |
|
ние dr и выражение (10.2) можно записать в виде |
|
R |
(10.3) |
Fdr = -dU . |
|
Следовательно, если известна функция U(r) , то из формулы (10.3) можно найти силу F по модулю и направлению.
Потенциальная энергия может быть определена исходя из (10.3) как
= −∫ R +
U Fdr C,
где C – постоянная интегрирования, т.е. потенциальная энергия определяется с точностью до некоторой произвольной постоянной. Это, однако, не отражается на физических законах, так как в них входит или разность потенциальных энер-
гий или производная U по координате. Поэтому потенциальную энергию тела в каком-то определенном положении считают равной нулю (выбирают нулевой уровень отсчета), а энергию тела в других положениях отсчитывают относитель-
но нулевого уровня.
Для консервативных сил
F = - |
∂U , |
F = - |
∂U , |
F = - |
∂U , |
|||
x |
¶x |
|
|
y |
|
¶y |
z |
¶z |
|
|
|
|
|
|
|||
или в векторном виде |
|
|
|
|
||||
F = -gradU , |
|
|
|
|
(10.4) |
|||
где |
|
|
|
|
|
|
|
|
gradU = |
∂U R |
+ |
∂U R |
∂U R |
(10.5) |
|||
¶x |
i |
¶y |
j + |
k |
||||
|
|
|
|
|
¶z |
|
||
Вектор, определяемый выражением (10.5), называется градиентом скаляра U .
Для него наряду с обозначением gradU применяется также обозначение
ÑU . Ñ означает символический вектор, называемый оператором Гамильтона
R |
∂ |
R |
|
∂ |
R |
|
∂ |
R |
|
|
Ñ = |
|
i |
+ |
|
j |
+ |
|
k . |
(10.6) |
|
¶x |
¶y |
¶z |
||||||||
|
|
|
|
|
|
|
Конкретный вид функции U зависит от характера силового поля. Напри-
мер, потенциальная энергия тела массой m , поднятого на высоту h над поверх-
ностью Земли, равна |
|
U = mgh , |
(10.7) |
где h отсчитывается от нулевого уровня, для которого U0 |
= 0. Выражение (10.7) |
вытекает непосредственно из того, что потенциальная энергия равна работе силы тяжести при падении тела с высоты h на поверхность Земли.
Так как начало отсчета выбирается произвольно, то потенциальная энергия может иметь отрицательное значение (кинетическая энергия всегда положитель-
на). Если принять за ноль потенциальную энергию тела, лежащего на поверхно-
сти Земли, то потенциальная энергия тела, находящегося на дне шахты (глубина h′), U = −mgh′.
Найдем потенциальную энергию упругодеформированного тела (пружины).
Сила упругости пропорциональна деформации
Fx упр = −kx ,
где Fx упр – проекция силы упругости на ось x ; k – коэффициент упругости
(жесткости), а знак минус указывает, что Fx упр направлена в сторону, противопо-
ложную деформации x .
По III закону Ньютона деформирующая сила равна по модулю силе упруго-
сти и противоположно ей направлена (рис.15),
т.е.
Fx = −Fx упр = kx .
Элементарная работа dA , совершаемая силой Fx
при бесконечно малой деформации dx, равна
dA = Fxdx = kxdx ,
а полная работа
x |
2 |
A = ∫kxdx = kx
2
0

идет на увеличение потенциальной энергии пружины. Таким образом, потенци-
альная энергия упруго деформированного тела равна
U = kx2 . 2
Потенциальная энергия системы, подобно кинетической энергии, является функцией состояния системы. Она зависит только от конфигурации системы и ее положения по отношению к внешним телам.
Полная механическая энергия системы – это энергия механического движения и взаимодействия и равна сумме кинетической и потенциальной энер-
гии
E = T + U .
Задача 1. На материальную точку массой m =1 кг действовала сила, изме-
|
R |
R |
R |
+ tk (Н). В начальный момент точка |
|
няющаяся по закону F |
= 12 t 3 i |
+ 6 t 2 j |
|||
R |
R |
|
|
|
|
= 2j −0,5k (м/с). Определите модуль импульса и кинетическую |
|||||
имела скорость v0 |
|||||
энергию точки в момент времени t =1 с.
Решение. Из второго закона Ньютона
R
FR = dp dt
выразим изменение импульса точки
R =
dp Fdt .
Для того, чтобы найти импульс точки в указанный момент времени проинтегри-
руем обе части этого равенства
R |
|
|
|
p |
R |
t |
R |
|
|
|
|
∫dp = ∫Fdt . |
|||
R |
|
0 |
|
p0 |
|
|
|
Подставим в полученную формулу выражение для вектора силы
R R |
t |
R |
R |
R |
R |
R |
|
t2 R |
||
p −p0 |
= ∫(12t3i |
+ 6t2 j |
+ tk)dt = 3t4i |
+ 2t3 j |
+ |
|
k |
|||
2 |
||||||||||
|
0 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||
и, учитывая, что

R |
R |
= m(2j - 0,5k) , |
p0 |
= mv0 |
получаем формулу для импульса точки
R |
R |
R |
|
t2 |
R |
|
R |
|
R |
R |
|
t2 R |
R |
R |
|
||
p = 3t |
4i |
+ 2t3j |
+ |
|
k |
+ p0 |
= 3t4i |
+ 2t3 j |
+ |
|
k |
+ 2mj |
- 0,5mk |
= |
|||
2 |
2 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||
R |
|
|
|
|
R |
|
|
2 |
|
R |
|
|
|
|
|
||
|
|
|
|
|
t |
|
|
|
|
|
|
|
|||||
= 3t4i |
+ |
(2t3 + |
2m)j + ( |
|
- 0,5m)k |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||
Подставив числовые значения, получим вектор импульса точки в указанный мо-
мент времени
R |
R |
|
R |
2 |
R R R |
|
×14 i |
+ (2 ×13 |
|
1 |
|
||
p = 3 |
+ 2 ×1)j + ( |
|
- 0,5 ×1)k = 3i + 4j . |
|||
2 |
||||||
|
|
|
|
|
Модуль импульса точки найдем по формуле
p = 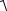
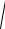 px2 + py2 + pz2 =
px2 + py2 + pz2 = 
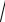 32 + 42 + 02 = 5 Н×с.
32 + 42 + 02 = 5 Н×с.
Кинетическую энергию точки в момент времени t = 1 с можно найти по
формуле
T = mv2 = m2v2 = p2 . 2 2m 2m
Подставив числовые значения, найдем
T = |
52 |
|
= 12,5 Дж . |
|
|||
2 ×1 |
|
||
Задача 2. Потенциальная энергия частицы имеет вид U = b(x2 + y2 ) . Най-
дите зависимость вектора силы, действующей на частицу, и ее модуля от коорди-
нат.
Решение. Сила и потенциальная энергия связаны между собой соотноше-
нием
F = -ÑU .
Исходя из этого выражения найдем проекции вектора силы на координатные оси
F |
= - |
∂U = -2bx и F |
= - |
∂U = -2by. |
|
x |
|
¶x |
y |
|
¶x |
|
|
|
|
||
Тогда зависимость вектора силы от координат будет иметь вид

F = −2bxi − 2byj .
Модуль найденной силы определяется выражением
F = 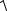
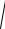 Fx2 + Fy2 = 2b
Fx2 + Fy2 = 2b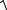
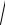 x2 + y2 .
x2 + y2 .
§ 11
Закон сохранения энергии
Закон сохранения энергии – результат обобщения многих эксперименталь-
ных данных. Идея этого закона принадлежит М.В. Ломоносову (1711–1765), из-
ложившему закон сохранения материи и движения, а количественная формули-
ровка закона сохранения энергии дана немецким врачом Ю. Майером (1814– 1878) и немецким естествоиспытателем Г. Гельмгольцем (1821–1894).
Рассмотрим систему материальных точек массами m1 , m2 , …, mn дви-
R |
R |
|
R |
′ |
′ |
′ |
жущихся со скоростями v1 |
, v2 |
, …, |
vn |
. Пусть F1 |
, F2 , …, |
Fn – равнодействующие |
внутренних консервативных сил, действующие на каждую из этих точек, а F1 , F2 , |
||||||
…, Fn – равнодействующие внешних сил, которые также будем считать консер-
вативными. Кроме того, будем считать, что на материальные точки действуют еще и внешние неконсервативные силы; равнодействующие этих сил, действую-
щих на каждую из материальных точек, обозначаем f1 , f2 , …, fn . При v << c
массы материальных точек постоянны и уравнения II закона Ньютона для этих точек следующие:
|
|
|
R |
|
R |
R |
R |
|
|
dv1 |
|
||||
m1 |
|
= F1′ + F1 + f1, |
|||||
|
dt |
|
|||||
|
|
|
R |
|
R |
R |
R |
|
|
|
dv2 |
||||
m |
|
|
= F′ + F |
+ f , |
|||
|
|
|
|||||
|
2 dt |
2 |
2 |
2 |
|||
....................................
R
dvn = R′ + R + R mn dt Fn Fn fn.
