
Физика / Физика / Механика. Лекции / lekcii_meh / glava7
.pdf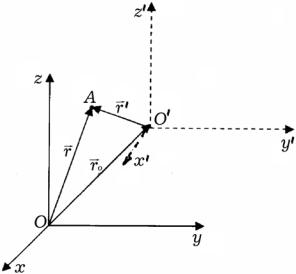
Глава 7 Элементы специальной теории относительности
§ 31
Преобразования Галилея. Механический принцип относительности
Если системы отсчета движутся относительно друг друга равномерно и прямолинейно и в одной из них справедливы законы динамики Ньютона, то эти системы являются инерциальными.
Механический принцип относительности (принцип относительности Гали-
лея) заключается в том, что во всех инерциальных системах отсчета законы классической динамики имеют одинаковую форму.
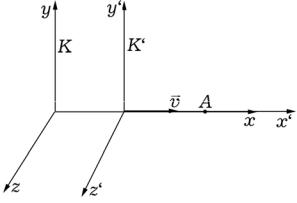
Рассмотрим две системы отсчета: инерциальную систему К (с координатами x, y, z), которую условно будем считать неподвижной, и систему K’ (с координатами x’, y’, z’), движущуюся относительно K со скоростью u ( ur = const ) равномерно и прямолинейно. Отсчет времени начнем с момента, когда начало координат обеих систем совпадают. Скорость u направлена
вдоль OO’, радиус-вектор, проведенный из О в О’, |
r = ut . |
|
0 |
Найдем связь между координатами произвольной точки А в обеих системах. |
|
Из рисунка видно, что |
|
rr = rr′+rr0 = r′+urt . |
(31.1) |
Уравнение (31.1) можно записать в проекциях на оси координат |
|
x = x′+uxt |
|
|
(31.2) |
y = y′+uyt . |
|
|
|
z = z′+uzt |
|
Уравнения (31.1) и (31.2) носят название преобразование координат Галилея.

В частном случае, когда система К’ движется со скоростью vr вдоль положительного направления оси х системы К, преобразование координат Галилея имеет вид
x = x′+vt
= ′ .
y y
z = z′
В классической механике предполагается, что ход времени не зависит от относительного движения систем отсчета, т.е. к преобразованиям (31.2) можно добавить еще одно уравнение
t = t′. |
(31.3) |
Продифференцируем выражение (31.1) по времени и получим уравнение
r r′ |
r |
(31.4) |
v = v |
+ u , |
которое представляет собой правило сложения скоростей в классической механике.
Ускорение в системе отсчета К
r |
r |
′ |
r |
|
|
|
r′ |
r |
|
|
dv |
d(v |
+u) |
|
dv |
|
|||||
a = |
|
= |
|
|
|
= |
|
= a′. |
|
|
dt |
dt |
|
|
dt |
|
|||||
Таким образом, ускорение точки А в системе К и K’, движущихся друг относи- |
||||||||||
тельно друга равномерно и прямолинейно, одинаково |
|
|||||||||
ar = ar′. |
|
|
|
|
|
|
|
(31.5) |
||
|
|
|
|
r |
= 0 |
|
′ |
= 0 . |
||
Следовательно, если a |
в системе К, то и в системе К’ a |
|||||||||
Таким образом, из соотношения (31.5) вытекает доказательство механического принципа относительности: уравнения динамики при переходе из одной инерциальной системы отсчета к другой не изменяются, т.е. являются инвариант- ными по отношению к преобразованиям координат. Галилей обратил внимание, что никакими механическими опытами, проведенными в данной инерциальной системе отсчета, нельзя установить, покоится ли она или движется прямолинейно и равномерно.
§ 32
Постулаты специальной теории относительности
Специальная теория относительности часто называется также релятивистской теорией, а специфические явления, описываемые этой теорией, – релятиви-
стскими эффектами.
В основе специальной теории относительности лежат постулаты Эйнштейна, сформулированные им в 1905 г.
I. Принцип относительности: никакие опыты, проведенные внутри данной инерциальной системы отсчета, не дают возможности обнаружить, покоится ли эта система или движется равномерно и прямолинейно; все законы природы инвариантны по отношению к переходу от одной инерциальной системы отсчета к другой.
II. Принцип инвариантности скорости света: скорость света в вакууме не зави-
сит от скорости движения источника света или наблюдателя и одинакова во всех инерциальных системах отсчета.
Первый постулат Эйнштейна, являясь обобщением механического принципа относительности Галилея на любые физические процессы.
Согласно второму постулату Эйнштейна, постоянство скорости света – функциональное свойство природы, которое констатируется как опытный факт.
§ 33
Преобразования Лоренца
Эйнштейн показал, что в теории относительности классические преобразования Галилея, описывающие переход от одной инерциальной системы отсчета к другой
K →K′ |
K′→K |
||
x′= x −vt |
x = x′+vt |
||
′ |
= y |
|
′ |
y |
y = y |
||
′ |
= z |
|
′ |
z |
z =z |
||
|
|
|
|
t′= t |
t =t′ |
||

заменяются преобразованиями Лоренца, удовлетворяющими постулатам Эйнштейна.
Эти преобразования предложены Лоренцем в 1904 г., еще до появления теории относительности, как преобразования, относительно которых уравнения Максвелла инвариантны.
Преобразования Лоренца имеют вид |
|
||||||||||||||||||||||
K →K′ |
|
|
|
K′→K |
|
|
|
|
|
|
|
|
|
||||||||||
|
′ |
|
|
|
x −vt |
|
|
|
|
′ |
|
|
|
′ |
|
||||||||
|
|
|
|
|
x +vt |
|
|
|
|
|
|
||||||||||||
x |
|
= |
|
|
|
|
|
x = |
|
|
|
|
|
|
|
|
|
||||||
|
|
1 |
−β |
2 |
|
|
1 −β |
2 |
|
|
|
|
|
||||||||||
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
||
|
y |
|
= y |
|
|
|
|
y = y |
|
|
|
|
|
|
β = |
v |
|
(33.1) |
|||||
′ |
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
z |
|
= z |
|
|
|
|
z = z |
|
|
|
|
|
|
|
c |
|
|||||||
|
|
|
|
t −βx c |
|
|
|
′ |
|
′ |
|
|
|
|
|
|
|||||||
t′ |
= |
t = |
t |
+βx c |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
1 |
−β |
2 |
|
|
|
|
|
1 |
−β |
2 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Принцип соответствия: при малых скоростях v << c (β<<1) |
преобразова- |
||||||||||||||||||||||
ния Лоренца переходят в классические преобразования Галилея, которые являются, следовательно, предельным случаем преобразований Лоренца.
Из преобразований Лоренца следует очень важный вывод о том, что как расстояние, так и промежуток времени между двумя событиями меняются при переходе от одной инерциальной системы отсчета к другой, в то время как в рамках преобразований Галилея эти величины считаются абсолютными, не изменяющимися при переходе от системы к системе.
Кроме того, в преобразованиях Лоренца пространственные координаты и время неразрывно связаны между собой, поэтому Эйнштейн вводит понятие че-
тырехмерного пространство-времени.
§ 34
Следствия из преобразований Лоренца 1. Одновременность событий в разных системах отсчета. Пусть в систе-
ме К в точках с координатами x1 и x2 в моменты времени t1 и t2 происходят два события. В системе К’ им соответствуют координаты x1′ и x′2 и момент времени

t1′ и t′2 . Если события в системе К происходят в одной точке ( x1 = x2 ) и являются одновременными ( t1 =t2 ), то согласно преобразованиям Лоренца, x1′ = x′2 и t1′ = t′2 , т.е. эти события являются одновременными и пространственно совпадаю-
щими для любой инерциальной системы отсчета.
Если события в системе К пространственно разобщены ( x1 ≠ x2 ), но одно-
временны ( t1 = t2 ), то в системе K’
x1′ = |
x1 −vt |
|
x′2 |
= |
x2 −vt |
|
|||
1 −β2 |
1 −β2 |
||||||||
|
|
|
|
|
|||||
t1′ = |
t1 −βx1 c |
t′2 |
= |
t2 −βx2 c |
|||||
|
|
||||||||
|
|
1 −β2 |
|
|
|
1 −β2 |
|||
x1′ ≠ x′2 |
t1′ ≠ t′2 |
||||||||
Таким образом, в системе K’ эти события, оставаясь пространственно разобщенными, оказываются и неодновременными.
2. Длительность событий в разных системах отсчета. Пусть в некоторых точке х, покоящейся относительно системе К, происходит событие, длительность которого τ = t2 −t1 . Длительность этого же события в системе K’
τ′= t′2 −t1′, |
(34.1) |
||||||
причем начало и конец события соответствуют |
|
||||||
t1′ = |
t1 −βx c |
|
|
|
|||
|
1 −β2 |
|
|||||
|
|
|
|
||||
t′2 = |
t2 −βx c |
. |
(34.2) |
||||
|
|
|
|||||
|
|
|
1 −β2 |
|
|||
Подставляя (34.2) в (34.1) получим |
|
||||||
′ |
|
|
τ |
|
|
||
|
|
1 −β2 . |
(34.3) |
||||
τ = |
|
||||||
Из соотношения (34.3) вытекает, что τ< τ′, т.е. длительность события, происходящее в некоторой точке, наименьшая в той инерциальной системе отсчета, относительно которой эта точка неподвижна. Следовательно, часы, движущиеся относительно инерциальной системы отсчета, идут медленнее покоящихся часов.

3. Длина тел для разных систем отсчета. Рассмотрим стержень, располо-
женный вдоль оси x′ и покоящийся относительно K, длина стержня в системе K’ будет l0′ = x′2 −x′2 , где x1′ и x′2 – не изменяющиеся со временем t′ координаты на-
чала и конца стержня, а индекс «0» показывает, что в системе отсчета K’ стержень покоится. Определим длину этого стержня в системе К, относительно которой он движется со скоростью v. Для этого необходимо измерить координаты его кон-
цов x1 и |
x2 в системе К в один и тот же момент времени t . Их разность |
|||||||
l = x2 −x1 |
и дает длину стержня в системе К. Используя преобразования Лоренца, |
|||||||
получим |
|
|
|
|
|
|
|
|
l0′ = x′2 −x1′ = |
x2 −vt |
− |
x1 −vt |
= |
x2 −x1 |
, |
||
1 −β2 |
1 −β2 |
|
||||||
|
|
|
|
|
1 −β2 |
|||
или |
|
|
|
|
|
|
|
|
l0′ = |
l |
. |
|
|
(34.4) |
|||
|
|
|
||||||
|
1 −β2 |
|
|
|
|
|
||
Поперечные размеры тела не зависят от скорости его движения и одинаковы во всех инерциальных системах отсчета. Таким образом, линейные размеры тела наименьшие в той инерциальной системе, относительно которой они покоятся.
4. Релятивистский закон сложения скоростей. Рассмотрим движение ма-
териальной точки в системе K′, в свою очередь движущейся относительно системы К со скоростью v. Определим скорость этой же точки в системе К. Если в системе К движение точки в каждый момент времени t определяется координатами x, y,z, а в системе K’ в момент времени t′ – координатами x′, y′,z′, то
ux = dxdt , uy = dydt , uz = dzdt
и
u′x = ddxt′′, u′y = ddyt′′, u′z = ddzt′′
представляют собой соответственно проекции на оси x, y,z, и x′, y′,z′ вектора
скорости рассматриваемой относительно систем К и К’. Согласно преобразованиям Лоренца (33.1)

dx = dx′+vdt′, dy = dy′, dz = dz′, dt = dt′+βdx′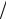 c . 1 −β2
c . 1 −β2
Произведя соответствующие преобразования, получаем релятивистский закон сложения скоростей специальной теории относительности.
K′→K |
|
|
|
|
|
K →K′ |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
′ |
|
|
|
|
|
|
|
|
u |
x |
−v |
|
|
|
|
|
|
ux |
= |
|
|
ux +v |
|
|
|
u′x = |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
1 −βu′x c |
|
|
||||||||||||||
1 |
+βu′x c |
|
|
||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u′y 1 −β |
2 |
|
|
|
|
uy |
1 −β |
2 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
uy |
= |
|
|
|
|
|
|
|
u′y = |
|
|
|
|
|
|
|
|
|
. |
(34.5) |
|
1 |
+βu′x c |
|
1 −βu′x c |
||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||
|
|
u′z 1 −β |
2 |
|
|
|
uz 1 −β |
2 |
|
|
|
|
|||||||||
|
= |
|
|
|
|
u′z = |
|
|
|
|
|
|
|||||||||
uz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 |
+βu |
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
c |
|
1 |
−β |
′ |
|
|
|
|
|
|
|||||||||||
|
|
x |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
ux c |
|
|
||||||||
Если материальная точка движения параллельно оси х, то скорость u относительно системы К совпадает с ux , а скорость u′ относительно K′ – с u′x . Те-
перь закон сложения скоростей примет вид
|
u′+v |
|
u′ = |
u −v |
|
|
u = |
|
, |
|
. |
(34.6) |
|
1+βu′ c |
1−βu′ c |
|||||
§ 35
Интервал между событиями
Преобразования Лоренца и следствия из них приводят к выводу об относительности длин и промежутков времени, значение которых в различных системах отсчета разное. В то же время относительный характер длин и промежутков времени в теории Эйнштейна означает относительность отдельных компонентов ка- кой-то реальной физической величины, не зависящей от системы отсчета, т.е. являющейся инвариантной по отношению к преобразованиям координат. В четырехмерном пространстве Эйнштейна, в котором каждое событие характеризуется четырьмя координатами (x, y,z, t), такой физической величиной является интер-
вал между двумя событиями
s = |
c2 (t |
2 |
−t )2 |
−(x |
2 |
−x )2 |
−(y |
2 |
−y )2 |
−(z |
2 |
−z )2 |
, |
(35.1) |
12 |
|
1 |
|
1 |
|
1 |
|
1 |
|
|

где  (x2 −x1 )2 −(y2 −y1 )2 −(z2 −z1 )2 =l12 – расстояние между точками обычного трехмерного пространства, в котором эти события произошли. Введя обозначение t12 = t2 −t1 , получим
(x2 −x1 )2 −(y2 −y1 )2 −(z2 −z1 )2 =l12 – расстояние между точками обычного трехмерного пространства, в котором эти события произошли. Введя обозначение t12 = t2 −t1 , получим
s12 =  c2 t122 −l122 .
c2 t122 −l122 .
Покажем, что интервал между двумя событиями одинаков во всех инерциальных системах отсчета. Обозначив t = t2 −t1 , x = x2 −x1 , y = y2 −y1 , z = z2 −z1 , выражение (35.1) можно записать в виде
s2 = c2 ( t)2 −( |
|
x)2 −( y)2 |
−( z)2 . |
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
Интервал между теми же событиями в системе K’ равен |
|
|||||||
(s' )2 |
= c2 ( t' )2 |
−( x' )2 −( |
y' )2 −( z' )2 |
|
|
|
(35.2) |
|
12 |
|
|
|
|
|
|
|
|
Согласно преобразованиям Лоренца (33.1) |
|
|
|
|
||||
′ |
x +v t |
, |
′ |
′ |
′ |
|
t −β x c |
. |
x = |
1 −β2 |
y = y , |
z = z , t |
|
= |
1 −β2 |
||
Подставив эти значения в (35.2), после элементарных преобразований получим, что
′ |
2 |
2 |
|
2 |
|
2 |
|
2 |
2 |
(s12 ) = c ( |
t) |
−( |
x) |
−( |
y) |
−( |
z) , |
||
т.е. |
|
|
|
|
|
|
|
|
|
′ |
2 |
2 |
|
|
|
|
|
|
|
(s12 ) |
|
= s12 . |
|
|
|
|
|
|
|
Инвариантность интервала означает, что, несмотря на относительность длины и промежутка времени, течение событий носит объективный характер и не зависит от системы отсчета.
§ 36
Основной закон релятивистской динамики материальной точки
На опытах с быстро движущимися электронами было установлено, что масса тела зависит от скорости его движения, а именно возрастает с увеличение скорости по закону
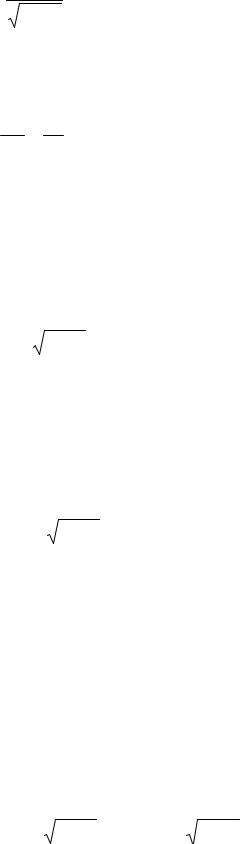
m = |
m0 |
, |
(36.1) |
1−β2 |
где m0 – масса покоя материальной точки.
Основной закон динамики Ньютона
Fr = ddtpr = dtd (mvr)
оказывается инвариантным по отношению к преобразованиям Лоренца, если в нем справа стоит производная по времени от релятивистского импульса.
Основной закон релятивистской динамики материальной точки имеет
вид
r |
d |
|
|
m0 |
|
vr |
|
|
|||
F = |
|
|
|
|
|
(36.2) |
|||||
|
|
|
|
|
2 |
||||||
|
dt |
|
1 −β |
|
|
|
|||||
|
|
|
|
|
|
||||||
или |
|
|
|
|
|
|
|
|
|
|
|
r |
dpr |
|
|
|
|
|
|
||||
F = |
|
|
|
, |
|
|
|
|
|
(36.3) |
|
dt |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||
где |
|
|
|
|
|
|
|
|
|
|
|
pr = mvr = |
|
m0 |
|
vr |
(36.4) |
||||||
|
1 −β2 |
||||||||||
|
|
|
|
|
|
|
|
|
|||
– релятивистский импульс материальной точки.
§ 37
Закон взаимосвязи массы и энергии
Найдем кинетическую энергию релятивистской частицы
dT = dA или dT = Fdrr. |
|
|
|
|
(37.1) |
|||||||
Учитывая, что drr = vrdt , и поставив в (37.1) выражение (36.2), получим |
||||||||||||
|
d |
m |
vr |
|
r |
r |
|
m |
vr |
|
|
|
dT = |
|
|
0 |
|
|
vdt = vd |
0 |
|
|
. |
||
|
|
|
2 |
|
|
2 |
||||||
|
|
|
1 −β |
|
|
|
1 −β |
|
||||
|
dt |
|
|
|
|
|
|
|||||
Преобразовав данное выражение с учетом того, что vdv = vdv, и формулы (36.1) придем к выражению

|
m0c2 |
|
|
|
2 |
|
|
|
dT = d |
|
|
|
|
|
= c |
dm , |
(37.2) |
|
2 |
|
2 |
|||||
|
1 −v |
c |
|
|
|
|
||
|
|
|
|
|
|
|
||
т.е. приращение кинетической энергии частицы пропорционально приращению ее массы.
Так как кинетическая энергия покоящейся частицы равна нулю, а ее масса равна массе m0 , то, проинтегрировав (37.2), получим
T = (m −m0 )c2 , |
|
|
(37.3) |
|||
или кинетическая энергия релятивистской частицы имеет вид |
|
|||||
|
2 |
|
1 |
|
|
|
T = m |
c |
|
|
|
−1 . |
(37.4) |
|
2 |
|||||
0 |
|
|
1 −β |
|
|
|
|
|
|
|
|
|
|
Выражение (37.4) при скоростях c >> v переходит в классическое
T = m20v2 .
А. Эйнштейн предположил, что выражение (37.2) справедливо не только для кинетической энергии материальной точки, но и для полной энергии, а имен-
но любое изменение массы |
m сопровождается изменением полной энергии ма- |
териальной точки, |
|
E = mc2 . |
(37.5) |
Отсюда Эйнштейн пришел к универсальной зависимости между полной энергии тела E и его массой m
E = mc2 = |
m0c2 |
. |
(37.6) |
|
|||
|
1 −β2 |
|
|
Уравнение (37.6), равно как и (37.5), выражает фундаментальный закон природы – закон взаимосвязи (пропорциональности) массы и энергии: полная энергия системы равна произведению ее массы на квадрат скорости света в вакууме.
Закон (37.6) можно, учитывая выражение (37.3), записать в виде
E = m0c2 +T,
откуда следует, что покоящееся тело ( T = 0 ) также обладает энергией
