
- •Минобрнауки россии
- •1.Цель работы
- •2.Основные положения
- •2.1.Точность методов и результатов измерений
- •2.2. Погрешность и неопределенность результата измерений
- •2.3. Рекомендации по применению Руководства в метрологии
- •Процедура вычисления неопределенности
- •2.4.Сравнительный анализ двух подходов к выражению точности измерений
- •3. Пример. Измерение силы электрического тока с помощью
- •Уравнение измерений
- •5.А. По типу а вычисляют стандартную неопределенность, обусловленную источниками неопределенности, имеющими случайный характер.
- •5.Б. По типу в вычисляют стандартные неопределенности, обусловленные источниками неопределенности, имеющим систематический характер. Закон распределения величин внутри границ считают равномерным.
- •5.В. Суммарную стандартную неопределенность вычисляют по формуле
- •5. Тесты – задания для самоконтроля
- •6. Глоссарий (словарь терминов)
5.А. По типу а вычисляют стандартную неопределенность, обусловленную источниками неопределенности, имеющими случайный характер.
Стандартную неопределенность напряжения, обусловленную источниками неопределенности, имеющими случайный характер, определяют по формуле
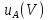 =
=
 ,
,
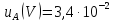 мВ;
мВ;
 = 0,034%/ (26)
= 0,034%/ (26)
Стандартную неопределенность силы тока, обусловленную источниками неопределенности, имеющими случайный характер, определяют по формуле
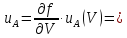
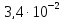 A,
A,
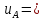 0,034% (27)
0,034% (27)
5.Б. По типу в вычисляют стандартные неопределенности, обусловленные источниками неопределенности, имеющим систематический характер. Закон распределения величин внутри границ считают равномерным.
Границы систематического смещения при измерениях напряжения, определенные при калибровке вольтметра, равны 3
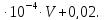 Тогда соответствующую стандартную
неопределенность вычисляют по формуле
Тогда соответствующую стандартную
неопределенность вычисляют по формуле
 мВ;
мВ;
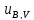 =
0,029% (28)
=
0,029% (28)
Границы, внутри которых лежит значение сопротивления шунта, определены при калибровке шунта и равны 7
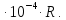 Тогда приR
=
Тогда приR
=
 соответствующую стандартную
неопределенность вычисляют по формуле
соответствующую стандартную
неопределенность вычисляют по формуле
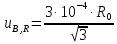 = 4,0
= 4,0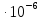 Ом;
Ом;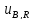 =
0,040 % (29)
=
0,040 % (29)
Границы изменения значения сопротивления шунта, обусловленного изменением температуры, равны
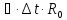 .
Соответствующую стандартную
неопределенность получают в соответствии
с формулой
.
Соответствующую стандартную
неопределенность получают в соответствии
с формулой
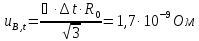 ,
,
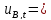 1,7
1,7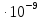 % (30)
% (30)
В дальнейшем этой составляющей неопределенности (виду ее малости по сравнении с другими составляющими) можно пренебречь.
Суммарную стандартную неопределенность, вычисленную по типу В, определяют по формуле
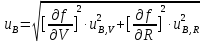 =
5,0
=
5,0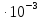 A;
A;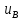 = 0,050 % (32)
= 0,050 % (32)
5.В. Суммарную стандартную неопределенность вычисляют по формуле
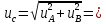 6,0
6,0 A,
A,
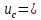 0,060 % (33)
0,060 % (33)
5.г. Эффективное число степеней свободы
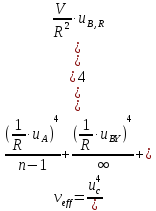 (34)
(34)
5.д. Коэффициент охвата получают по формуле
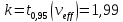 (35)
(35)
5.e. Расширенную неопределенность определяют следующим образом
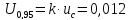 A,
A,
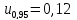 (36)
(36)
Переход от характеристик погрешности к неопределенности измерений.
6.а. Используя оценки характеристик погрешности, полученные в п.п. 3 и 4 данного примера, можно продемонстрировать получение оценок неопределенностей в соответствии с п. 4.г настоящей рекомендации.
Схема 1.
I = 9,984 A,
S
= 3,4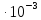 A,
A,
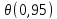 = 9,5
= 9,5 A,
A,
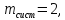
n = 10
I = 9,984 A,
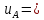 S
= 3,4
S
= 3,4 A,
A,
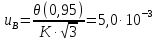 A,
A,
K =1,1; p = 0,95,
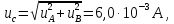


В данном примере неопределенности измерений, вычисленные в п.5 данного примера в соответствии с Руководством, совпадают с их оценками, полученными по схеме 1.
Схема 2.
I = 9,984 A,
 =
0,012 А.
=
0,012 А.
р= 0,95
I = 9,984 A,
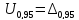 =
0,012 А.
=
0,012 А.
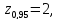
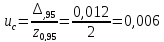 A.
A.

В данном примере разность неопределенностей измерений, вычисленных в п.5 данного примера в соответствии с Руководством, и их оценок, полученных по схеме 2, меньше погрешности округления при вычислениях.
4. Вопросы и задания по теме
«Точность и неопределенность измерений»
Что понимается под определением «метод» в Стандарте 5725 и как оно согласуется с ФЗ-102 «Об обеспечении единства измерений» от 26.06. 2008 г.?
Что нового внесено в понятие «точность» по ГОСТ5725?
Охарактеризуйте понятия повторяемости и воспроизводимости.
Какие показатели свойств повторяемости и воспроизводимости введены для крайних условий измерений?
По каким причинам методы описания погрешности измерений в последнее время перестали удовлетворять ряду требований, предъявляемых к решаемым в теоретической метрологии задачам?
К чему сведены основные положения Руководства?
Каковы числовые оценки неопределенности?
Что понимается под категориями неопределенности?
Какова процедура вычисления неопределенности по типу А?
Какова процедура вычисления неопределенности по типу В?
В чем сходство двух подходов к выражению точности?
В чем различие двух подходов к выражению точности?
Каков основной вывод из практики применения двух подходов к выражению точности измерений?
Под эгидой каких семи международных организаций разработано «Руководство по выражению неопределенности измерения»?
Решить задачу «Измерение силы электрического тока с помощью вольтметра и токового шунта». По исходным данным (таблица 3) в соответствии с вышеизложенной методикой:
Найти результат измерений.
Провести анализ источников погрешности результата измерений.
Вычислить характеристики погрешности результата измерений.
Вычисление неопределенности измерений.
По типу А вычислить стандартную неопределенность, обусловленную источниками неопределенности, имеющими случайный характер.
По типу В вычислить стандартные неопределенности, обусловленные источниками неопределенности, имеющим систематический характер. Закон распределения величин внутри границ считают равномерным.
Определить суммарную стандартную неопределенность, эффективное число степеней свободы и коэффициент охвата.
Построить схемы перехода от характеристик погрешности к неопределенности измерений.
Таблица 3. Исходные данные
|
Номер варианта |
ряд
значений
| |||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 | |
|
0 |
100,68 |
100,65 |
100,79 |
100,64 |
100,63 |
100,84 |
100,60 |
100,68 |
100,83 |
100,67 |
|
при его калибровке
для I= 10Aи | ||||||||||
|
1 |
100,68 |
100,56 |
100,79 |
100,64 |
100,73 |
100,94 |
100,60 |
100,68 |
100,73 |
100,76 |
|
при его калибровке
для I= 10Aи | ||||||||||
|
2 |
100,68 |
100,65 |
100,97 |
100,84 |
100,63 |
100,94 |
100,60 |
100,88 |
100,83 |
100,76 |
|
при его калибровке
для I= 10Aи | ||||||||||
|
3 |
100,68 |
100,65 |
100,89 |
100,67 |
100,63 |
100,94 |
100,90 |
100,68 |
100,83 |
100,76 |
|
при его калибровке
для I= 10Aи | ||||||||||
|
4 |
100,68 |
100,75 |
100,79 |
100,64 |
100,65 |
100,64 |
100,60 |
100,68 |
100,83 |
100,86 |
|
при его калибровке
для I= 10Aи | ||||||||||
|
5 |
100,78 |
100,65 |
100,79 |
100,64 |
100,83 |
100,91 |
100,60 |
100,68 |
100,73 |
100,76 |
|
при его калибровке
для I= 10Aи | ||||||||||
|
6 |
100,68 |
100,75 |
100,79 |
100,74 |
100,63 |
100,94 |
100,67 |
100,88 |
100,83 |
100,76 |
|
при его калибровке
для I= 10Aи | ||||||||||
|
7 |
100,68 |
100,65 |
100,69 |
100,64 |
100,63 |
100,94 |
100,70 |
100,86 |
100,83 |
100,76 |
|
при его калибровке
для I= 10Aи | ||||||||||
|
8 |
100,68 |
100,75 |
100,79 |
100,94 |
100,63 |
100,93 |
100,60 |
100,68 |
100,87 |
100,76 |
|
при его калибровке
для I= 10Aи | ||||||||||
|
9 |
100,88 |
100,65 |
100,79 |
100,64 |
100,93 |
100,94 |
100,60 |
100,68 |
100,83 |
100,65 |
|
при его калибровке
для I= 10Aи | ||||||||||

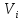 в милливольтах,
в милливольтах,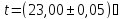 ,
,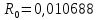 Ом.
Ом.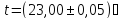 ,
,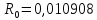 Ом.
Ом.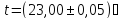
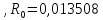 Ом.
Ом.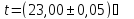 ,
,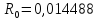 Ом.
Ом.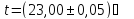 ,
,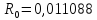 Ом.
Ом. ,
,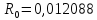 Ом.
Ом. ,
,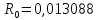 Ом.
Ом. ,
, Ом.
Ом.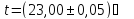 ,
, Ом.
Ом.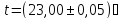 ,
, Ом.
Ом.